Comparing PyTorch Embeddings with Custom Embeddings

machine learning
fastai
python
In this notebook I compare the code required to build a collaborative filtering model using PyTorch Embeddings and custom embeddings.
Author

Vishal Bakshi

Published

June 25, 2024

Background

In this notebook I’ll work through the following “Further Research” prompt at the end of Chapter 8 of the fastai textbook:

Take a look at all the differences between the Embedding version of DotProductBias and the create_params version, and try to understand why each of those changes is required. If you’re not sure, try reverting each change to see what happens (even the type of brackets used in forward has changed!)

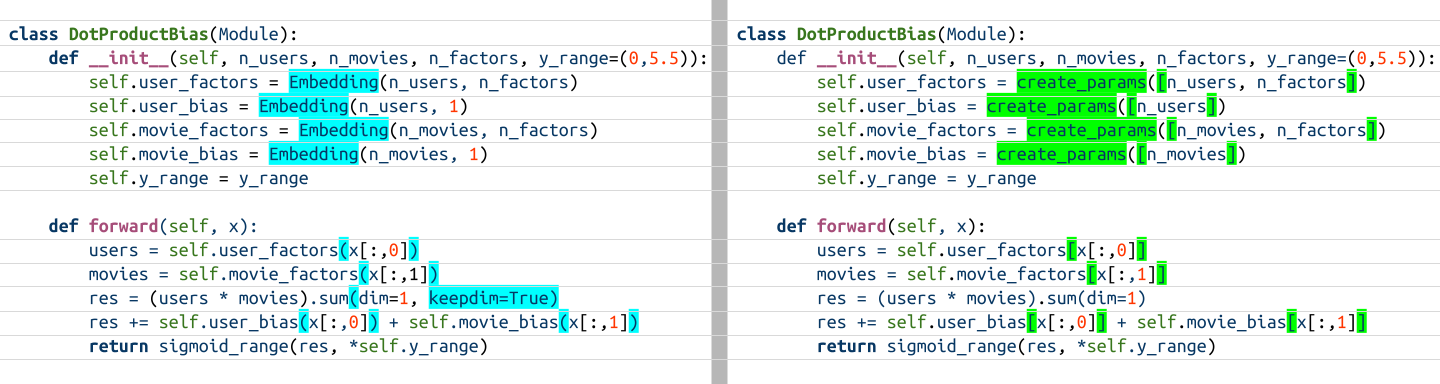
Visual Inspection of Code

I’ll start by visually inspecting and annotating the differences between the two functions (I made this visual in Google Slides using the beautiful Ubuntu Mono font):

Visual inspection of two DotProductBias Modules

Visual inspection of two DotProductBias Modules

Stepping Through the Code

Next, I’ll step through each DotProductBias implementation’s code using real data. I was getting an SSL error when using untar_data(URLs.ML_100k) so I manually downloaded the data.

from fastai.collab import *
from fastai.tabular.all import *
!unzip /content/ml-100k.zip
path = Path('/content/ml-100k')
ratings = pd.read_csv(path/'u.data', delimiter='\t', header=None, names=['user', 'movie', 'rating', 'timestamp'])
movies = pd.read_csv(path/'u.item', delimiter='|', encoding='latin-1', usecols=(0,1), names=('movie', 'title'), header=None)
ratings = ratings.merge(movies)
dls = CollabDataLoaders.from_df(ratings, item_name='title', bs=64)
dls.show_batch()
user title rating
0 713 Wings of the Dove, The (1997) 3
1 788 In & Out (1997) 2
2 270 Benny & Joon (1993) 5
3 682 Searching for Bobby Fischer (1993) 5
4 543 Fantasia (1940) 4
5 535 Contact (1997) 5
6 463 Waiting for Guffman (1996) 3
7 326 Man Who Would Be King, The (1975) 5
8 712 Around the World in 80 Days (1956) 4
9 804 North by Northwest (1959) 5 
n_users = len(dls.classes['user'])
n_movies = len(dls.classes['title'])
n_factors = 5

n_users, n_movies, n_factors
(944, 1665, 5)
xb, yb = dls.one_batch()
xb.shape, yb.shape
(torch.Size([64, 2]), torch.Size([64, 1]))
def create_params(size):
  return nn.Parameter(torch.zeros(*size).normal_(0, 0.01))

Creating User Latent Factors

The first line in each implementation creates the (untrained) latent factors for users. For all variable names, I’ll append _emb for the Embedding model implementation and _cp for the create_params implementation.

The first difference between the two implementations (other than the obvious that one uses Embedding and the other uses create_params) is that Embedding is given two arguments to determine its size (ni and nf), whereas create_params is given one list with both sizes. I’ll illustrate this by showing the error thrown by each one when called without passing arguments:

user_factors_emb = Embedding(n_users, n_factors)
user_factors_cp = create_params([n_users, n_factors])

user_factors_emb, user_factors_cp.shape
(Embedding(944, 5), torch.Size([944, 5]))
Embedding()
---------------------------------------------------------------------------
TypeError                                 Traceback (most recent call last)
<ipython-input-21-e7169ece36a6> in <cell line: 1>()
----> 1 Embedding()

TypeError: Embedding.__init__() missing 2 required positional arguments: 'ni' and 'nf'
create_params()
---------------------------------------------------------------------------
TypeError                                 Traceback (most recent call last)
<ipython-input-22-bbdd11ed5a1f> in <cell line: 1>()
----> 1 create_params()

TypeError: create_params() missing 1 required positional argument: 'size'

Creating User Bias

The next line in each model creates the bias object for users:

The main difference here is that the output dimension of 1 is specified for the Embedding but only a single size is given to create_params, the reason being that create_params is just a tensor which will return a tensor when indexed, whereas Embedding needs an explicit output feature size. The consequence of this will be seen later on in the forward pass.

user_bias_emb = Embedding(n_users, 1)
user_bias_cp = create_params([n_users])

user_bias_emb, user_bias_cp.shape
(Embedding(944, 1), torch.Size([944]))
user_bias_emb(xb[:,0]).shape, user_bias_cp[xb[:,0]].shape
(torch.Size([64, 1]), torch.Size([64]))

Creating Movie Latent Factors and Bias

The next two lines in each model do the same thing but for the movies (items):

movie_factors_emb = Embedding(n_movies, n_factors)
movie_factors_cp = create_params([n_movies, n_factors])

movie_bias_emb = Embedding(n_movies, 1)
movie_bias_cp = create_params([n_movies])

movie_factors_emb, movie_factors_cp.shape, movie_bias_emb, movie_bias_cp.shape,
(Embedding(1665, 5),
 torch.Size([1665, 5]),
 Embedding(1665, 1),
 torch.Size([1665]))

Forward Pass

There are two differences in how the forward method is defined when using Embedding versus create_params:

  • You have to call an Embedding but index the tensor created by create_params.
  • You have to specify keepdim=True for the dot product in the Embedding model when using sum but don’t need to do so in the create_params model.

The first bullet point can be illustrated easily:

(
    movie_factors_emb(xb[:,1]).shape, # call Embeddings to get output (a tensor)
    movie_factors_cp[xb[:,1]].shape # index `create_params` output (a tensor)
)
(torch.Size([64, 5]), torch.Size([64, 5]))

The second bullet point is illustrated by not passing keepdim=True to the sum call for the Embedding output product and seeing what happens:

The output product here has a single dimension with 64 items in that dimension. In the next line of the forward pass, we will try to add the bias vectors to this product:

res_emb = (user_factors_emb(xb[:,0]) * movie_factors_emb(xb[:,1])).sum(dim=1)
res_emb.shape
torch.Size([64])
res_emb += user_bias_emb(xb[:,0]) + movie_bias_emb(xb[:,1])
---------------------------------------------------------------------------
RuntimeError                              Traceback (most recent call last)
<ipython-input-39-e454f67ea331> in <cell line: 1>()
----> 1 res_emb += user_bias_emb(xb[:,0]) + movie_bias_emb(xb[:,1])

RuntimeError: output with shape [64] doesn't match the broadcast shape [64, 64]

But that doesn’t work because the bias Embedding outputs a tensor with dimensions 64 x 1. We need that unit axis at the end in order to allow for tensor addition to take place. keepdim=True preserves that unit axis:

res_emb = (user_factors_emb(xb[:,0]) * movie_factors_emb(xb[:,1])).sum(dim=1, keepdim=True) # unit axis preserved
res_emb += user_bias_emb(xb[:,0]) + movie_bias_emb(xb[:,1])
res_emb.shape
torch.Size([64, 1])

We don’t get this issue when using create_params because we didn’t specify a unit axis to begin with.

Recall that when creating the user and movie bias in the model’s __init__ method, only a single size is given to create_params:

self.user_bias = create_params([n_users])
...
self.movie_bias = create_params([n_movies])

When we perform the dot product between users and movies in the create_params model, we don’t need to preserve that second dimension:

res_cp = (user_factors_cp[xb[:,0]] * movie_factors_cp[xb[:,1]]).sum(dim=1) # keepdim=False
res_cp += user_bias_cp[xb[:,0]] + movie_bias_cp[xb[:,1]]
res_cp.shape
torch.Size([64])

The output of the create_params model has a single dimension, while the output of the Embedding model has an additional unit axis.

I’m displaying the visual inspection again to recap the differences we saw in the implementation of the two models:

Visual inspection of two DotProductBias Modules

Visual inspection of two DotProductBias Modules

Training Each Model

To cap off this experiment, I’ll show that both models train similarly:

class DotProductBiasEmb(Module):
  def __init__(self, n_users, n_movies, n_factors, y_range=(0,5.5)):
    self.user_factors = Embedding(n_users, n_factors)
    self.user_bias = Embedding(n_users, 1)
    self.movie_factors = Embedding(n_movies, n_factors)
    self.movie_bias = Embedding(n_movies, 1)
    self.y_range = y_range

  def forward(self, x):
    users = self.user_factors(x[:,0])
    movies = self.movie_factors(x[:,1])
    res = (users * movies).sum(dim=1, keepdim=True)
    res += self.user_bias(x[:,0]) + self.movie_bias(x[:,1])
    return sigmoid_range(res, *self.y_range)
model_emb = DotProductBiasEmb(n_users, n_movies, n_factors=50)
learn_emb = Learner(dls, model_emb, loss_func=MSELossFlat())
learn_emb.fit_one_cycle(5, 5e-3, wd=0.1)
epoch train_loss valid_loss time
0 0.889749 0.947634 00:14
1 0.663791 0.881707 00:16
2 0.526889 0.861133 00:22
3 0.465532 0.845524 00:14
4 0.452247 0.841644 00:13 
class DotProductBiasCP(Module):
  def __init__(self, n_users, n_movies, n_factors, y_range=(0, 5.5)):
    self.user_factors = create_params([n_users, n_factors])
    self.user_bias = create_params([n_users])
    self.movie_factors = create_params([n_movies, n_factors])
    self.movie_bias = create_params([n_movies])
    self.y_range = y_range

  def forward(self, x):
    users = self.user_factors[x[:,0]]
    movies = self.movie_factors[x[:,1]]
    res = (users * movies).sum(dim=1)
    res += self.user_bias[x[:,0]] + self.movie_bias[x[:,1]]
    return sigmoid_range(res, *self.y_range)
model_cp = DotProductBiasCP(n_users, n_movies, n_factors=50)
learn_cp = Learner(dls, model_cp, loss_func=MSELossFlat())
learn_cp.fit_one_cycle(5, 5e-3, wd=0.1)
epoch train_loss valid_loss time
0 0.892142 0.941568 00:15
1 0.681598 0.885387 00:14
2 0.526930 0.868586 00:15
3 0.448445 0.854881 00:17
4 0.445660 0.849560 00:14

The top 5 movies (based on learned bias) for each model are the same. Note that since DotProductBiasEmb uses Embeddings for the bias, I have to access the weight of the Embedding so I can sort the values.

# Embedding model
movie_bias_emb = learn_emb.model.movie_bias.weight.squeeze()
idxs = movie_bias_emb.argsort(descending=True)[:5]
[dls.classes['title'][i] for i in idxs]
["Schindler's List (1993)",
 'Titanic (1997)',
 'Shawshank Redemption, The (1994)',
 'Good Will Hunting (1997)',
 'Star Wars (1977)']
# create_params model
movie_bias_cp = learn_cp.model.movie_bias.squeeze()
idxs = movie_bias_emb.argsort(descending=True)[:5]
[dls.classes['title'][i] for i in idxs]
["Schindler's List (1993)",
 'Titanic (1997)',
 'Shawshank Redemption, The (1994)',
 'Good Will Hunting (1997)',
 'Star Wars (1977)']

Final Thoughts

As always, I am reminded of the value that Jupyter Notebooks can bring to the coding (and learning) experience. Being able to run each line of code in the two variants of the DotProductBias model while writing out formatted explanatory text solidifies my understanding of how a batch of data passes through each model. Telling a story while writing code is a satisfying experience.

This exercise also illustrates how much the behavior of a model changes with a seemingly small difference—-both Embedding and create_params output tensors (and allow for the same type of training) but they are of different shapes; the construction of Embeddings and the inputs to create_params are different as well. These differences trickle through the entire model as well as the post-training analysis.

I hope you enjoyed this blog post! Follow me on Twitter @vishal_learner.