Training Models on the MovieLens 25M Dataset

deep learning
machine learning
fastai
python
In this notebook I train models using 5 different architectures on the 25 million rating MovieLens dataset and compare performance and results.
Author

Vishal Bakshi

Published

July 13, 2024

Background

In this notebook I’ll work through the following prompt from the “Further Research” section of Chapter 8 (Collaborative Filtering) from the fastai textbook:

Complete this notebook using the full MovieLens dataset, and compare your results to online benchmarks. See if you can improve your accuracy. Look on the book’s website and the fast.ai forums for ideas. Note that there are more columns in the full dataset–see if you can use those too (the next chapter might give you ideas).

Here’s a summary of my results in this notebook:

Arch Metric Metric Value
DotProductBias MSE 0.654875
DotProductBiasCE Accuracy 35%
Random Forest (baseline) Accuracy 29%
Random Forest (additional columns) Accuracy 30%
Neural Net Accuracy 38%

Load the Data

The data is formatted slightly differently than the 100k subset (main difference is the columns are labeled differently).

from fastai.collab import *
from fastai.tabular.all import *
from google.colab import drive
drive.mount('/content/drive')
Drive already mounted at /content/drive; to attempt to forcibly remount, call drive.mount("/content/drive", force_remount=True).
path = Path('/content/drive/MyDrive/movielens25m')
path.ls()
(#12) [Path('/content/drive/MyDrive/movielens25m/tags.csv'),Path('/content/drive/MyDrive/movielens25m/ratings.csv'),Path('/content/drive/MyDrive/movielens25m/movies.csv'),Path('/content/drive/MyDrive/movielens25m/genome-tags.csv'),Path('/content/drive/MyDrive/movielens25m/genome-scores.csv'),Path('/content/drive/MyDrive/movielens25m/links.csv'),Path('/content/drive/MyDrive/movielens25m/README.txt'),Path('/content/drive/MyDrive/movielens25m/rf_baseline_vars.pkl'),Path('/content/drive/MyDrive/movielens25m/rf_additional_vars.pkl'),Path('/content/drive/MyDrive/movielens25m/to_nn.pkl')...]
ratings = pd.read_csv(path/'ratings.csv')
ratings.head()
userId movieId rating timestamp
0 1 296 5.0 1147880044
1 1 306 3.5 1147868817
2 1 307 5.0 1147868828
3 1 665 5.0 1147878820
4 1 899 3.5 1147868510 
ratings['movieId'].unique().shape, ratings['userId'].unique().shape
((59047,), (162541,))
movies = pd.read_csv(path/'movies.csv')
movies.head()
movieId title genres
0 1 Toy Story (1995) Adventure|Animation|Children|Comedy|Fantasy
1 2 Jumanji (1995) Adventure|Children|Fantasy
2 3 Grumpier Old Men (1995) Comedy|Romance
3 4 Waiting to Exhale (1995) Comedy|Drama|Romance
4 5 Father of the Bride Part II (1995) Comedy 
movies['movieId'].unique().shape
(62423,)
ratings = ratings.merge(movies[['movieId', 'title']])
ratings.head()
userId movieId rating timestamp title
0 1 296 5.0 1147880044 Pulp Fiction (1994)
1 3 296 5.0 1439474476 Pulp Fiction (1994)
2 4 296 4.0 1573938898 Pulp Fiction (1994)
3 5 296 4.0 830786155 Pulp Fiction (1994)
4 7 296 4.0 835444730 Pulp Fiction (1994) 
dls = CollabDataLoaders.from_df(ratings, item_name='title', bs=1024)
dls.show_batch()
userId title rating
0 18382 Goldfinger (1964) 3.0
1 47473 Eyes Wide Shut (1999) 0.5
2 132661 Garden State (2004) 3.0
3 68944 X-Men Origins: Wolverine (2009) 0.5
4 126422 Animal Kingdom (2010) 3.5
5 122810 Hotel Rwanda (2004) 3.5
6 8458 Sherlock Holmes (2009) 4.0
7 21172 Indiana Jones and the Temple of Doom (1984) 4.0
8 94712 Dark Knight, The (2008) 3.5
9 88335 Chicken Run (2000) 2.0 
dls.classes.keys()
dict_keys(['userId', 'title'])
n_users = len(dls.classes['userId'])
n_movies = len(dls.classes['title'])

n_users, n_movies
(162542, 58959)

Training Using Different Approaches

DotProductBias with Embeddings

The first architecture I’ll use is the DotProductBias with Embeddings:

class DotProductBias(Module):
    def __init__(self, n_users, n_movies, n_factors, y_range=(0,5.5)):
        self.user_factors = Embedding(n_users, n_factors)
        self.user_bias = Embedding(n_users, 1)
        self.movie_factors = Embedding(n_movies, n_factors)
        self.movie_bias = Embedding(n_movies, 1)
        self.y_range = y_range

    def forward(self, x):
        users = self.user_factors(x[:,0])
        movies = self.movie_factors(x[:,1])
        res = (users * movies).sum(dim=1, keepdim=True)
        res += self.user_bias(x[:,0]) + self.movie_bias(x[:,1])

        return sigmoid_range(res, *self.y_range)

I’ll use the same number of epochs, learning rate and weight decay as the textbook training example:

model = DotProductBias(n_users, n_movies, 50)
learn = Learner(dls, model, loss_func=MSELossFlat())
learn.fit_one_cycle(5, 5e-3, wd=0.1)
epoch train_loss valid_loss time
0 0.718568 0.750686 1:31:29
1 0.721771 0.743393 1:50:58
2 0.675583 0.713021 1:51:44
3 0.627697 0.671975 1:48:30
4 0.608647 0.654875 1:41:17

When using the 100k subset the lowest validation MSE I got was about 0.836. A validation MSE of 0.654875 is about a 22% reduction.

After rounding the predictions to the nearest 0.5, the model has a validation accuracy of about 30%. Yikes! That’s terrible.

preds, targs = learn.get_preds(dl=dls.valid)
preds
tensor([[3.1825],
        [3.1959],
        [3.6061],
        ...,
        [1.6408],
        [3.3054],
        [3.4723]])
rounded_preds = (preds / 0.5).round() * 0.5
rounded_preds
tensor([[3.0000],
        [3.0000],
        [3.5000],
        ...,
        [1.5000],
        [3.5000],
        [3.5000]])
targs
tensor([[3.0000],
        [5.0000],
        [3.5000],
        ...,
        [1.0000],
        [2.0000],
        [3.5000]])
(rounded_preds == targs).float().mean()
tensor(0.2931)

If I round to the nearest integer, the validation accuracy increases to about 36%. Still not great.

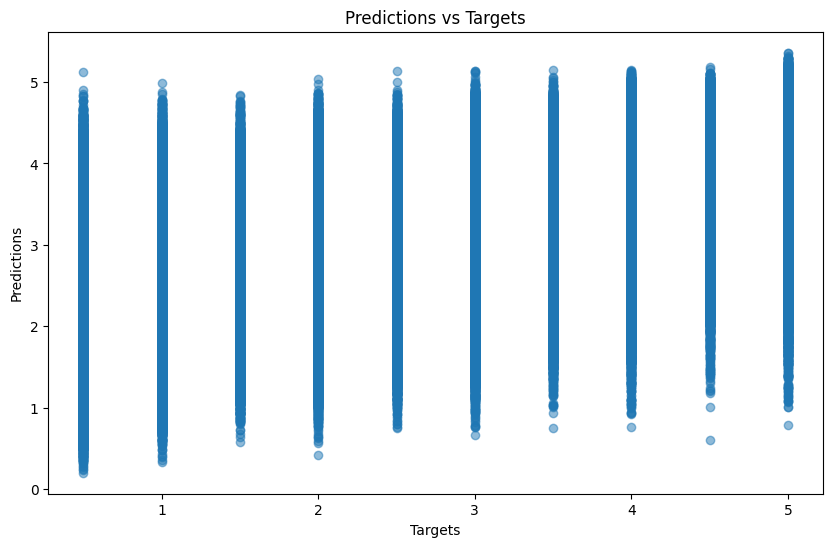
(preds.round(decimals=0) == targs).float().mean()
tensor(0.3581)

Plotting predictions versus the targets shows the weak relationship between the two:

def plot_preds_v_targs(preds, targs):
  plt.figure(figsize=(10, 6))
  plt.scatter(targs.detach().numpy().squeeze(), preds.detach().numpy().squeeze(), alpha=0.5)
  plt.xlabel('Targets')
  plt.ylabel('Predictions')
  plt.title('Predictions vs Targets')
  plt.show()
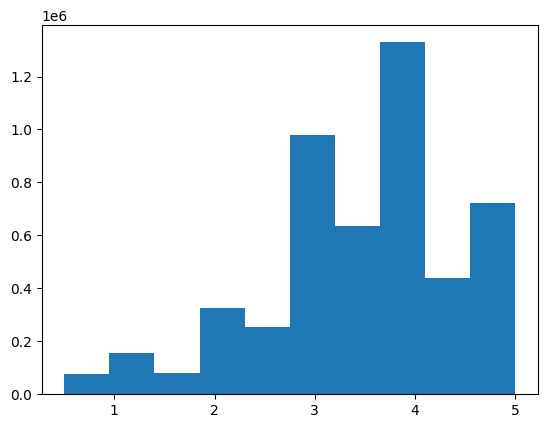
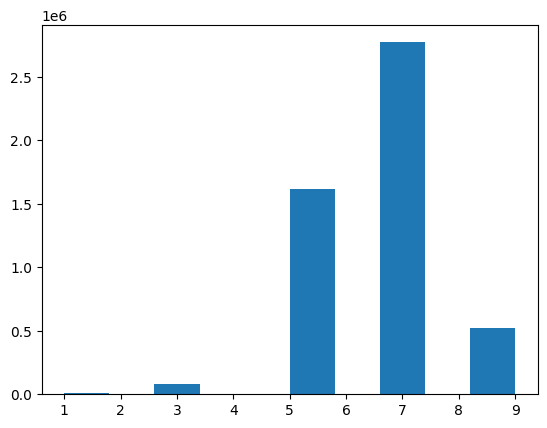
plot_preds_v_targs(preds, targs)

Here’s the distribution of the ratings targets for the ~5M validation records:

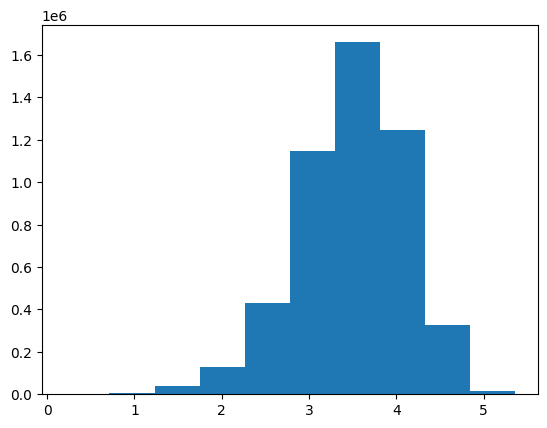
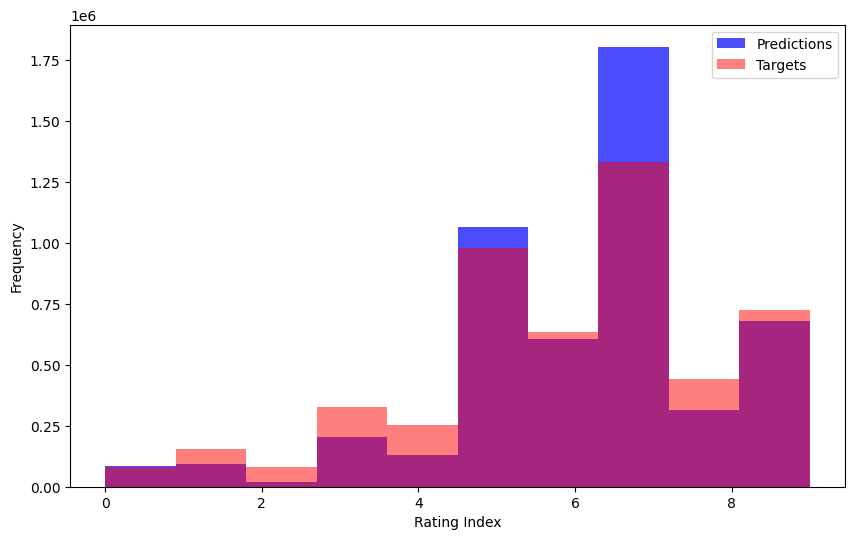
plt.hist(targs.detach().numpy().squeeze());

There are considerably fewer predictions less than 3 and greater than 4:

plt.hist(preds.detach().numpy().squeeze());

Let’s hope for better luck with other architectures!

DotProductBiasCE (for Cross Entropy Loss)

I’ll use the same architecture that I created for another Further Research prompt, with the slight modification that instead of projecting the dot product to 5 ratings I’ll project them to 10 ratings (as there are ten 0.5-increment ratings in the dataset: 0.5, 1.0, 1.5, 2.0, 2.5, 3.0, 3.5, 4.0, 4.5, 5.0).

class DotProductBiasCE(Module):
  def __init__(self, n_users, n_movies, n_factors):
    self.user_factors = Embedding(n_users, n_factors)
    self.user_bias = Embedding(n_users, 1)
    self.movie_factors = Embedding(n_movies, n_factors)
    self.movie_bias = Embedding(n_movies, 1)
    self.linear = nn.Linear(1, 10)

  def forward(self, x_cat, x_cont):
    x = x_cat
    users = self.user_factors(x[:,0])
    movies = self.movie_factors(x[:,1])
    res = (users * movies).sum(dim=1, keepdim=True)
    res += self.user_bias(x[:,0]) + self.movie_bias(x[:,1])
    return self.linear(res)

I’ll use the same training setup as I did with the 100k subset, but with a larger batch size (otherwise it takes much longer to train). Note that using the same learning rate for a batch size of 1024 as a batch size of 64 will likely not result in optimal training.

dls = TabularDataLoaders.from_df(
    ratings[['userId', 'title', 'rating']],
    procs=[Categorify],
    cat_names=['userId','title'],
    y_names=['rating'],
    y_block=CategoryBlock,
    bs=1024)
b = dls.one_batch()
len(b), b[0].shape, b[1].shape, b[2].shape
(3, torch.Size([1024, 2]), torch.Size([1024, 0]), torch.Size([1024, 1]))
dls.vocab
[0.5, 1.0, 1.5, 2.0, 2.5, 3.0, 3.5, 4.0, 4.5, 5.0]
dls.show_batch()
userId title rating
0 64415 Jumpin' Jack Flash (1986) 2.0
1 10508 Lord of the Rings: The Return of the King, The (2003) 4.5
2 126649 Frances Ha (2012) 4.0
3 119566 Elizabeth (1998) 3.0
4 77160 Snake Eyes (1998) 5.0
5 99259 Untouchables, The (1987) 3.5
6 3726 Myth of Fingerprints, The (1997) 2.0
7 100959 Meet the Parents (2000) 3.5
8 134993 Nightmare on Elm Street, A (1984) 1.0
9 117798 Doubt (2008) 4.0 
n_users = len(dls.classes['userId'])
n_movies = len(dls.classes['title'])

n_users, n_movies
(162542, 58959)

Training with Cross Entropy Loss on the 25M dataset resulted in a model with about 35% validation accuracy, about 6% less than the 41% achieved on the 100k subset. The model is not showing signs of overfitting so I could have trained it for more epochs and potentially gained more accuracy.

model = DotProductBiasCE(n_users, n_movies, n_factors=50)
learn = Learner(dls, model, loss_func=CrossEntropyLossFlat(), metrics=accuracy)
learn.fit_one_cycle(5, 0.1, wd=0.1)
epoch train_loss valid_loss accuracy time
0 1.919933 1.924016 0.288326 1:04:57
1 1.914961 1.927970 0.284413 1:33:05
2 1.900328 1.901067 0.294077 1:19:56
3 1.837524 1.847121 0.313432 1:40:26
4 1.704779 1.740781 0.354360 1:18:08

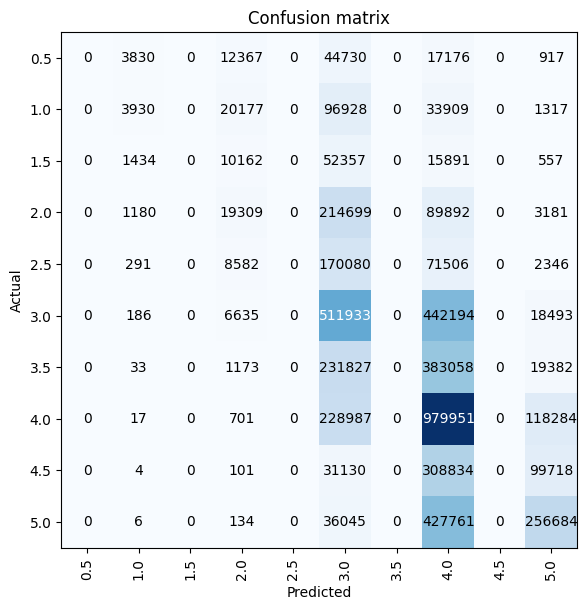
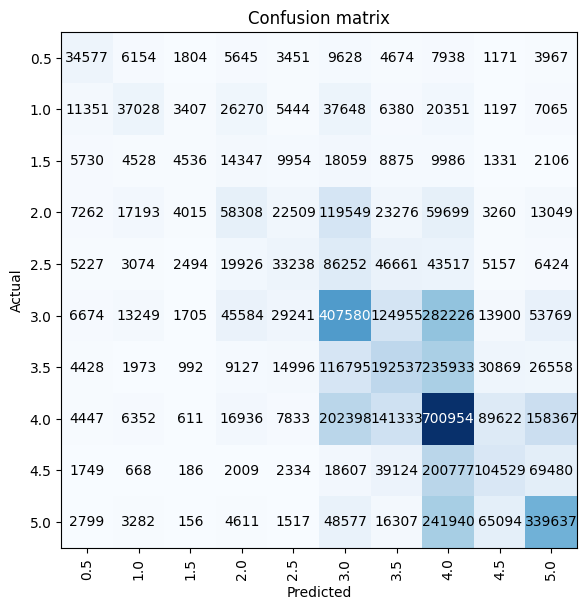
3’s and 4’s were the most correctly predicted ratings by this model, with the model performing quite badly for other ratings—in particular, the model did not predict any 0.5, 1.5, 2.5, 3.5, or 4.5 ratings.

interp = ClassificationInterpretation.from_learner(learn)
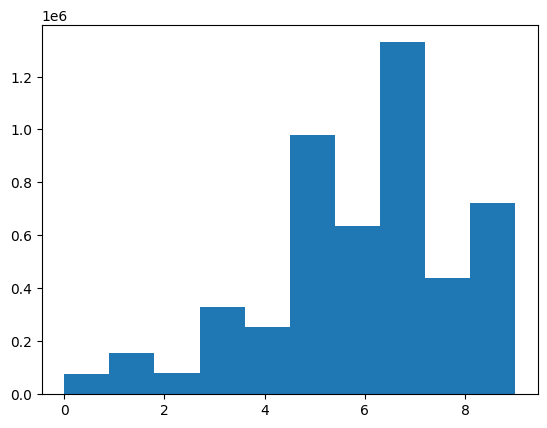
interp.plot_confusion_matrix(figsize=(6, 6))

preds, targs = learn.get_preds(dl=learn.dls.valid)

By far the most common predicted rating was 4.0 (the 7th category in the vocab). Again, I’ll note the gaps between the bars where the 0.5-increment ratings are absent from the model’s predictions.

plt.hist(preds.argmax(dim=1));

While the most common target is also 4.0, note that it’s frequency is about half that in the prediction distribution.

plt.hist(targs.squeeze());

Random Forest (baseline)

As an additional exercise I’ll train a random forest on the userId, movieId and rating fields. In the following section, I’ll add some of the additional fields available and see if that improves the forest’s performance. I’ll follow the approach given in Chapter 9 of the fastai textbook.

Setup

I’ll start by creating a TabularPandas object with a random split:

splits = RandomSplitter(seed=42)(range_of(ratings))
len(splits), len(splits[0]), len(splits[1])
(2, 20000076, 5000019)
to = TabularPandas(
    ratings[['userId', 'title', 'rating']],
    procs=[Categorify, FillMissing],
    cat_names=['userId', 'title'],
    cont_names=None,
    y_names='rating',
    y_block=CategoryBlock,
    splits=splits)
len(to.train), len(to.valid)
(20000076, 5000019)
to.show(3)
userId title rating
8613915 11056 Divergent (2014) 2.0
20221395 128803 Town, The (2010) 4.0
21140474 56442 Jack Ryan: Shadow Recruit (2014) 3.0 
to.items.head(3) # coded values
userId title rating
8613915 11056 13670 3
20221395 128803 53868 7
21140474 56442 24434 5 
to.vocab # 10 possible ratings
[0.5, 1.0, 1.5, 2.0, 2.5, 3.0, 3.5, 4.0, 4.5, 5.0]
# defining variables
xs,y = to.train.xs, to.train.y
valid_xs,valid_y = to.valid.xs, to.valid.y

xs.shape, y.shape, valid_xs.shape, valid_y.shape
((20000076, 2), (20000076,), (5000019, 2), (5000019,))
#save_pickle(path/'rf_baseline_vars.pkl', (xs, y, valid_xs, valid_y))

I’ll create helper functions to calculate accuracy of the model:

def acc(pred,y): return (pred == y).mean()
def m_acc(m, xs, y): return acc(m.predict(xs), y)
from sklearn.ensemble import RandomForestClassifier

def rf(xs, y, n_estimators=4, max_samples=10_000, max_features=0.5,
       min_samples_leaf=5, **kwargs):
  return RandomForestClassifier(n_jobs=-1, n_estimators=n_estimators, max_samples=max_samples,
              max_features=max_features, min_samples_leaf=min_samples_leaf, oob_score=True).fit(xs, y)

Training Results

Since training on the full data will likely take awhile, I’ll first fit a random forest with 4 trees and a max of ten thousand samples for each tree, which takes about a minute to train and results in a 22% validation accuracy which is not bad!

m = rf(xs, y, n_estimators=4, max_samples=10_000)
m_acc(m, xs, y), m_acc(m, valid_xs, valid_y)
(0.22450199689241182, 0.22447194700660136)

Doubling the number of trees (to 8) increases the validation accuracy to 24% (+2%).

m = rf(xs, y, n_estimators=8, max_samples=10_000)
m_acc(m, xs, y), m_acc(m, valid_xs, valid_y)
(0.24051508604267305, 0.24045988625243225)

Tripling the number of trees (to 12) gives a smaller boost (1%) to the validation accuracy (25%).

m = rf(xs, y, n_estimators=12, max_samples=10_000)
m_acc(m, xs, y), m_acc(m, valid_xs, valid_y)
(0.25057739780588834, 0.25026804898141386)

As the number of samples increases by 10_000 (while keeping n_estimators=4) the validation accuracy increases by about 0.2-0.5% each time.

for samples in [20_000, 30_000, 40_000]:
  m = rf(xs, y, n_estimators=4, max_samples=samples)
  print(f'samples: {samples}; train acc: {m_acc(m, xs, y)}; valid acc: {m_acc(m, valid_xs, valid_y)}')
samples: 20000; train acc: 0.23020222523154413; valid acc: 0.22950612787671407
samples: 30000; train acc: 0.23159146995241417; valid acc: 0.2313785207616211
samples: 40000; train acc: 0.23347261280407133; valid acc: 0.23300171459348454

Next, I’ll train a random forest using the parameters given in Chapter 9 of the text (40 trees, 200_000 samples), keeping in mind that was for a 400k row dataset, so not optimized for 25M rows of data. I’ll then double n_estimators and max_samples to see which combination works best. I’m not using a for-loop like above since my Colab instance kept crashing so I’ll fit the different random forests in individual cells.

40 trees and 200_000 samples results in a validation accuracy of 28% (+3% from the previous best achieved by 12 trees and 10_000 samples).

trees = 40
samples = 200_000
m = rf(xs, y, n_estimators=trees, max_samples=samples)
print(f'samples: {samples}; trees: {trees}; train acc: {m_acc(m, xs, y):.2f}; valid acc: {m_acc(m, valid_xs, valid_y):.2f}')
samples: 200000; trees: 40; train acc: 0.29; valid acc: 0.28

Doubling the number of trees from 40 to 80 results in a 29% validation accuracy (+1%). It took about 35 minutes to train and predict.

trees = 80
samples = 200_000
m = rf(xs, y, n_estimators=trees, max_samples=samples)
print(f'samples: {samples}; trees: {trees}; train acc: {m_acc(m, xs, y):.2f}; valid acc: {m_acc(m, valid_xs, valid_y):.2f}')
samples: 200000; trees: 80; train acc: 0.29; valid acc: 0.29

Doubling the number of samples used to 400_000 while keeping the number of trees at 40 achieves the same validation accuracy (29%) and took about 21 minutes for training and inference.

trees = 40
samples = 400_000
m = rf(xs, y, n_estimators=trees, max_samples=samples)
print(f'samples: {samples}; trees: {trees}; train acc: {m_acc(m, xs, y):.2f}; valid acc: {m_acc(m, valid_xs, valid_y):.2f}')
samples: 400000; trees: 40; train acc: 0.30; valid acc: 0.29

Doubling the number of trees to 80 with 400_000 samples achieves the same accuracy of 29% (while taking 42 minutes for training and inference).

trees = 80
samples = 400_000
m = rf(xs, y, n_estimators=trees, max_samples=samples)
print(f'samples: {samples}; trees: {trees}; train acc: {m_acc(m, xs, y):.2f}; valid acc: {m_acc(m, valid_xs, valid_y):.2f}')
samples: 400000; trees: 80; train acc: 0.30; valid acc: 0.29

I’ll increase the number of samples significantly to 2_000_000. I’ll keep the number of trees at 40 for now since increasing that number doesn’t seem to improve validation accuracy significantly.

This results in a validation accuracy of 29%.

It doesn’t seem like increasing the number of trees or samples will significantly change the validation accuracy.

trees = 40
samples = 2_000_000
m = rf(xs, y, n_estimators=trees, max_samples=samples)
print(f'samples: {samples}; trees: {trees}; train acc: {m_acc(m, xs, y):.2f}; valid acc: {m_acc(m, valid_xs, valid_y):.2f}')
samples: 2000000; trees: 40; train acc: 0.33; valid acc: 0.29
def rf_feat_importance(m, df):
  return pd.DataFrame({'cols': df.columns, 'imp': m.feature_importances_}
                      ).sort_values('imp', ascending=False)

With this data and model, userId is almost twice as important as the movie title.

rf_feat_importance(m, xs)
cols imp
0 userId 0.640407
1 title 0.359593

Random Forest (with additional data)

There a few additional columns available that may improve the performance of the random forest:

  • ratings.csv has a timestamp column.
    • This is easy to incorporate as there is one value per rating.
  • movies.csv has a genres column.
    • There are multiple pipe-separated genres per movie, I’ll pick one genre per movie.
  • tags.csv has tags associated with each movie by users.
    • There are multiple tags for each movie/user pair, I’ll pick one tag per user/movie pair.
  • genome-scores.csv has genome-tags associated with each movie.
    • There are multiple genome-tags per movie, so I’ll pick the genome-tag with the highest score for each movie.
# do str.split on `movies` before merging with `ratings` since it has fewer rows
movies['genres'] = movies['genres'].str.split('|', n=1).str[0]
ratings = ratings.merge(movies)
ratings.head() # peep the new `genres` column with a single genre
userId movieId rating timestamp title genres
0 1 296 5.0 1147880044 Pulp Fiction (1994) Comedy
1 3 296 5.0 1439474476 Pulp Fiction (1994) Comedy
2 4 296 4.0 1573938898 Pulp Fiction (1994) Comedy
3 5 296 4.0 830786155 Pulp Fiction (1994) Comedy
4 7 296 4.0 835444730 Pulp Fiction (1994) Comedy 
ratings.shape
(25000095, 6)

Only a fraction (~10%) of all of the ratings.csv userIds are captured in tags.csv, whereas about 75% of the movieIds are captured in tags.csv. I’ll pick the most frequent tag for each movie and merge with the ratings data.

tags = pd.read_csv(path/'tags.csv')
ratings['userId'].unique().shape, tags['userId'].unique().shape
((162541,), (14592,))
ratings['movieId'].unique().shape, tags['movieId'].unique().shape
((59047,), (45251,))

There’s about 8k tags that are different only because of capitalization—I’ll set all tags to lower case:

tags['tag'].unique().shape, tags['tag'].str.lower().unique().shape
((73051,), (65465,))
tags['tag'] = tags['tag'].str.lower()
# thanks Claude 3.5 Sonnet
# this was MUCH faster than using groupby + agg
most_common_tags = (
    tags.groupby(['movieId', 'tag'])
    .size()
    .reset_index(name='count')
    .sort_values(['movieId', 'count'], ascending=[True, False])
    .drop_duplicates('movieId')
    .drop('count', axis=1)
)

most_common_tags.head()
movieId tag
78 1 pixar
155 2 robin williams
168 3 fishing
185 4 chick flick
207 5 steve martin 
ratings.shape
(25000095, 6)
ratings = ratings.merge(most_common_tags, on=['movieId'], how='left')
print(ratings.shape)
ratings.head()
(25000095, 7)
userId movieId rating timestamp title genres tag
0 1 296 5.0 1147880044 Pulp Fiction (1994) Comedy quentin tarantino
1 3 296 5.0 1439474476 Pulp Fiction (1994) Comedy quentin tarantino
2 4 296 4.0 1573938898 Pulp Fiction (1994) Comedy quentin tarantino
3 5 296 4.0 830786155 Pulp Fiction (1994) Comedy quentin tarantino
4 7 296 4.0 835444730 Pulp Fiction (1994) Comedy quentin tarantino

Only a very small fraction of ratings are without a tag:

ratings['tag'].isna().sum()
83417
genome_scores = pd.read_csv(path/'genome-scores.csv')
genome_tags = pd.read_csv(path/'genome-tags.csv')
genome_scores.head()
movieId tagId relevance
0 1 1 0.02875
1 1 2 0.02375
2 1 3 0.06250
3 1 4 0.07575
4 1 5 0.14075 
genome_tags.head()
tagId tag
0 1 007
1 2 007 (series)
2 3 18th century
3 4 1920s
4 5 1930s

I’ll use the most relevant genome tag for each movie:

most_common_genomes = (
    genome_scores.sort_values(['movieId', 'relevance'], ascending=[True, False])
    .drop_duplicates('movieId')
)

most_common_genomes.head()
movieId tagId relevance
1035 1 1036 0.99925
1156 2 29 0.97600
3156 3 901 0.97525
4499 4 1116 0.97525
5412 5 901 0.96025 
genome_scores['movieId'].unique().shape, most_common_genomes.shape
((13816,), (13816, 3))

With that sorted, I’ll get the actual tag text:

most_common_genomes = most_common_genomes.merge(genome_tags)
most_common_genomes.shape
(13816, 4)
most_common_genomes = most_common_genomes.rename(columns={'tag': 'genome_tag'})
most_common_genomes.head()
movieId tagId relevance genome_tag
0 1 1036 0.99925 toys
1 1920 1036 0.99575 toys
2 3114 1036 0.99850 toys
3 78499 1036 0.99875 toys
4 81981 1036 0.84225 toys 
most_common_genomes['movieId'].unique().shape
(13816,)

and add it to the main DataFrame:

ratings.shape
(25000095, 7)
ratings = ratings.merge(most_common_genomes[['movieId', 'genome_tag']], how='left')
ratings.head()
userId movieId rating timestamp title genres tag genome_tag
0 1 296 5.0 1147880044 Pulp Fiction (1994) Comedy quentin tarantino hit men
1 3 296 5.0 1439474476 Pulp Fiction (1994) Comedy quentin tarantino hit men
2 4 296 4.0 1573938898 Pulp Fiction (1994) Comedy quentin tarantino hit men
3 5 296 4.0 830786155 Pulp Fiction (1994) Comedy quentin tarantino hit men
4 7 296 4.0 835444730 Pulp Fiction (1994) Comedy quentin tarantino hit men

With the DataFrame established, I’ll create a TabularPandas object using the same seed (42) as before for splits.

splits = RandomSplitter(seed=42)(range_of(ratings))
len(splits), len(splits[0]), len(splits[1])
(2, 20000076, 5000019)
to = TabularPandas(
    ratings[['userId', 'title', 'timestamp', 'genres', 'tag', 'genome_tag', 'rating']],
    procs=[Categorify, FillMissing],
    cat_names=['userId', 'title', 'genres', 'tag', 'genome_tag'],
    cont_names=['timestamp'],
    y_names='rating',
    y_block=CategoryBlock,
    splits=splits)
len(to.train), len(to.valid)
(20000076, 5000019)
to.show(3)
userId title genres tag genome_tag timestamp rating
8613915 11056 Divergent (2014) Adventure dystopia vampire human love 1422282990 2.0
20221395 128803 Town, The (2010) Crime ben affleck crime 1312046717 4.0
21140474 56442 Jack Ryan: Shadow Recruit (2014) Action cia tom clancy 1491438306 3.0 
to.items.head(3) # coded values
userId title timestamp genres tag genome_tag rating
8613915 11056 13670 1422282990 3 4536 791 3
20221395 128803 53868 1312046717 7 1983 183 7
21140474 56442 24434 1491438306 2 3241 769 5 
xs,y = to.train.xs, to.train.y
valid_xs,valid_y = to.valid.xs, to.valid.y

xs.shape, y.shape, valid_xs.shape, valid_y.shape
((20000076, 6), (20000076,), (5000019, 6), (5000019,))

Using the additional columns has increased the validation accuracy from 22% (when using only movieId and userId) to 23.7% (when using the additional columns timestamp, tag, genome_tag and genres).

m = rf(xs, y, n_estimators=4, max_samples=10_000)
m_acc(m, xs, y), m_acc(m, valid_xs, valid_y)
(0.23697224950545187, 0.23664510074861717)

Doubling the number of trees to 8 yields a validation accuracy of 25% (a ~1% increase from before).

m = rf(xs, y, n_estimators=8, max_samples=10_000)
m_acc(m, xs, y), m_acc(m, valid_xs, valid_y)
(0.2500907496551513, 0.24987865046112825)

Tripling the number of trees to 12 yields a validation accuracy of 26% (a ~1% increase from before).

m = rf(xs, y, n_estimators=12, max_samples=10_000)
m_acc(m, xs, y), m_acc(m, valid_xs, valid_y)
(0.25923971488908343, 0.2590440156327406)

For every 10_000 sample increase (with 4 trees) the validation accuracy improves between 0.02-0.6%.

for samples in [20_000, 30_000, 40_000]:
  m = rf(xs, y, n_estimators=4, max_samples=samples)
  print(f'samples: {samples}; train acc: {m_acc(m, xs, y)}; valid acc: {m_acc(m, valid_xs, valid_y)}')
samples: 20000; train acc: 0.24337092519048428; valid acc: 0.24275807751930542
samples: 30000; train acc: 0.2467036625260824; valid acc: 0.24597866528107193
samples: 40000; train acc: 0.24714531084781877; valid acc: 0.24619486445951505

Increasing the number of trees to 40 and the number of samples to 200_000 results in a validation accuracy of 30% (the baseline random forest validation accuracy was 28%).

trees = 40
samples = 200_000
m = rf(xs, y, n_estimators=trees, max_samples=samples)
print(f'samples: {samples}; trees: {trees}; train acc: {m_acc(m, xs, y):.2f}; valid acc: {m_acc(m, valid_xs, valid_y):.2f}')
samples: 200000; trees: 40; train acc: 0.30; valid acc: 0.30

Doubling the number of trees results in a validation accuracy of 30%. (baseline was 29%).

trees = 80
samples = 200_000
m = rf(xs, y, n_estimators=trees, max_samples=samples)
print(f'samples: {samples}; trees: {trees}; train acc: {m_acc(m, xs, y):.2f}; valid acc: {m_acc(m, valid_xs, valid_y):.2f}')
samples: 200000; trees: 80; train acc: 0.31; valid acc: 0.30

Doubling the number of samples to 400_000 with 40 trees gets a validation accuracy of 30% (baseline was 29%).

trees = 40
samples = 400_000
m = rf(xs, y, n_estimators=trees, max_samples=samples)
print(f'samples: {samples}; trees: {trees}; train acc: {m_acc(m, xs, y):.2f}; valid acc: {m_acc(m, valid_xs, valid_y):.2f}')
samples: 400000; trees: 40; train acc: 0.31; valid acc: 0.30

Doubling the number of trees to 80 with 400_000 samples does not improve the validation accuracy of 30%.

trees = 80
samples = 400_000
m = rf(xs, y, n_estimators=trees, max_samples=samples)
print(f'samples: {samples}; trees: {trees}; train acc: {m_acc(m, xs, y):.2f}; valid acc: {m_acc(m, valid_xs, valid_y):.2f}')
samples: 400000; trees: 80; train acc: 0.32; valid acc: 0.30

Even after increasing the number of samples to 2M, the validation accuracy stays at 30%.

trees = 40
samples = 2_000_000
m = rf(xs, y, n_estimators=trees, max_samples=samples)
print(f'samples: {samples}; trees: {trees}; train acc: {m_acc(m, xs, y):.2f}; valid acc: {m_acc(m, valid_xs, valid_y):.2f}')
samples: 2000000; trees: 40; train acc: 0.36; valid acc: 0.30

It’s interesting (and a bit concerning) to note that timestamp is the most important feature for this model—it’s 6-7 times as important as the movie title.

rf_feat_importance(m, xs)
cols imp
5 timestamp 0.443988
0 userId 0.346306
1 title 0.073165
3 tag 0.060231
4 genome_tag 0.056996
2 genres 0.019314

I’ll follow fastai’s Chapter 9 approach to determining which columns’ values differ the most between the training and validation set.

df_dom = pd.concat([xs, valid_xs])
is_valid = np.array([0]*len(xs) + [1]*len(valid_xs))
m = rf(df_dom, is_valid, n_estimators=40, max_samples=400_000)

timestamp is the most important feature when distinguishing between the training and validation set. I’ll remove it to see if it improves training.

rf_feat_importance(m, df_dom)
cols imp
5 timestamp 0.313090
0 userId 0.311026
1 title 0.131196
3 tag 0.106029
4 genome_tag 0.099509
2 genres 0.039150 
m = rf(xs.drop('timestamp', axis=1), y, n_estimators=40, max_samples=400_000)

After removing timestamp, userId surges to the top, being 6 times as important as the 2nd-most important feature (title). The validation accuracy stays at 30%.

rf_feat_importance(m, xs.drop('timestamp', axis=1))
cols imp
0 userId 0.674746
1 title 0.113734
3 tag 0.096440
4 genome_tag 0.088569
2 genres 0.026510 
m_acc(m, valid_xs.drop('timestamp', axis=1), valid_y)
0.2971844706990113

Neural Net (tabular_learner)

Next, I’ll train a neural net on this data and see how it performs. I’ll also use the embeddings from the neural net later on to train a new random forest.

df_nn = ratings.drop(['timestamp', 'movieId'], axis=1)
df_nn.head()
userId rating title genres tag genome_tag
0 1 5.0 Pulp Fiction (1994) Comedy quentin tarantino hit men
1 3 5.0 Pulp Fiction (1994) Comedy quentin tarantino hit men
2 4 4.0 Pulp Fiction (1994) Comedy quentin tarantino hit men
3 5 4.0 Pulp Fiction (1994) Comedy quentin tarantino hit men
4 7 4.0 Pulp Fiction (1994) Comedy quentin tarantino hit men 
procs_nn = [Categorify, FillMissing]
cat_nn = ['userId', 'genres', 'tag', 'genome_tag']
cont_nn = None
splits = RandomSplitter(seed=42)(range_of(df_nn))
len(splits), len(splits[0]), len(splits[1])
(2, 20000076, 5000019)
to_nn = TabularPandas(
    df_nn,
    procs_nn,
    cat_names=cat_nn,
    cont_names=None,
    splits=splits,
    y_names='rating',
    y_block=CategoryBlock)
dls = to_nn.dataloaders(1024)
dls.show_batch()
userId genres tag genome_tag rating
0 149149 Documentary boxing documentary 4.0
1 5588 Action conspiracy conspiracy 5.0
2 67949 Adventure animation computer animation 3.0
3 61069 Action satire satire 0.5
4 43620 Comedy 1930s 1930s 3.0
5 161519 Action natalie portman hit men 4.0
6 155206 Crime tom hanks oscar (best directing) 4.0
7 91508 Drama england skinhead 4.0
8 76347 Drama clint eastwood western 5.0
9 30987 Crime serial killer oscar (best directing) 5.0 
learn = tabular_learner(dls, layers=[1000, 500], loss_func=CrossEntropyLossFlat(), metrics=accuracy)
learn.lr_find()
SuggestedLRs(valley=0.0003311311302240938)

The GPU RAM stayed at around 3.5/15.0 GB during training so if I wanted to train again I’d use a larger batch size. The neural net achieved a 38% validation accuracy, better than the random forest (30%) and the DotProductBiasCE model (35%).

learn.fit_one_cycle(5, 2e-2)
epoch train_loss valid_loss accuracy time
0 1.576747 1.615499 0.359292 19:06
1 1.557086 1.605259 0.362625 18:48
2 1.514029 1.582966 0.369193 19:03
3 1.422227 1.559873 0.377868 18:50
4 1.328115 1.570342 0.382583 18:48

The neural net is much better at predicting a diverse range of ratings (whereas DotProductBiasCE did not predict any ratings ending with .5). Like the DotProductBiasCE model, the neural net’s most accurate prediction was 4. Unlike DotProductBiasCE the diagonal in the confusion matrix is somewhat darker than the non-diagonal, showing that the model is doing a better job of correctly predicting ratings (as exhibited by the higher overall accuracy).

interp = ClassificationInterpretation.from_learner(learn)
interp.plot_confusion_matrix(figsize=(6, 6))

preds, targs = learn.get_preds(dl=learn.dls.valid)

The distribution of predictions has no gaps—the model predicts all possible ratings.

plt.figure(figsize=(10, 6))
plt.hist(preds.argmax(dim=1).squeeze(), alpha=0.7, color='blue', label='Predictions');
plt.hist(targs.squeeze(), alpha=0.5, color='red', label='Targets');
plt.legend()
plt.xlabel('Rating Index')
plt.ylabel('Frequency')
plt.show()

Random Forest with Neural Net Embeddings

The final approach I was hoping to implement was using the embeddings from the neural net to create additional columns and using them to train a random forest, as done in this Medium post.

However, I ran into some RAM and disk space issues. To illustrate, I’ll show the four Embeddings that the model has learned, which totals an output of 955 values.

learn.model.embeds
ModuleList(
  (0): Embedding(162542, 600)
  (1): Embedding(21, 9)
  (2): Embedding(9856, 276)
  (3): Embedding(841, 70)
)

The smallest data type (without receiving an error) I was able to use when passing a column of xs through an Embedding was int32 which takes up 4 bytes per element. With 20M rows in the training set, outputting 955 values each 4 bytes large would take up about 76 GB of storage.

20e6*4*955/1e9
76.4

Another 5M rows of the validation set (each with 955 Embedding outputs) would bump that up to over 100GB. Kaggle provides 73GB of disk space and 30GB of RAM. Google Colab provides 107GB of disk space and 13GB of RAM.

Handling these sorts of RAM/disk space issues is something I want to learn about and experiment with in the future, after which I can return to this scale of a dataset in an attempt to train it.

Final Thoughts

Training models on the full MovieLens 25M rating dataset using Kaggle and/or Google Colab was tough. Training a single model took up to 9 hours (in the case of DotProductBias), so just getting through five different architectures required patience (on top of a lot of runtime crashes due to RAM maxing out). However, it was still fun to see how these different architectures behaved and performed during training. Here’s a summary of my results:

Arch Metric Metric Value
DotProductBias MSE 0.654875
DotProductBiasCE Accuracy 35%
Random Forest (baseline) Accuracy 29%
Random Forest (additional columns) Accuracy 30%
Neural Net Accuracy 38%

In the fastai textbook, the MSE of DotProductBias on the 100k rating subset was about 0.8 and in my experiments with DotProductBiasCE (Cross-Entropy Loss) the Accuracy for DotProductBiasCE was about 40%. The 25M DotProductBias beat the 100k subset’s MSE and the 25M neural net was competitive with the 100k subset’s accuracy.

There’s still performance gains that I didn’t pursue (for example, training the neural net for more epochs or trying a different number of hidden layer sizes), but I’m satisfied with the breadth of my experiments and learning experience.

I hope you enjoyed this blog post! Following me on Twitter @vishal_learner.