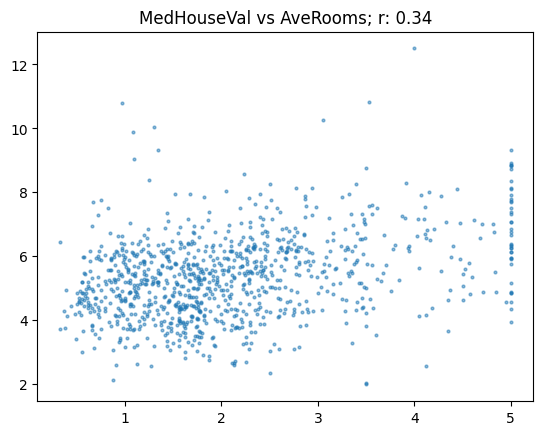
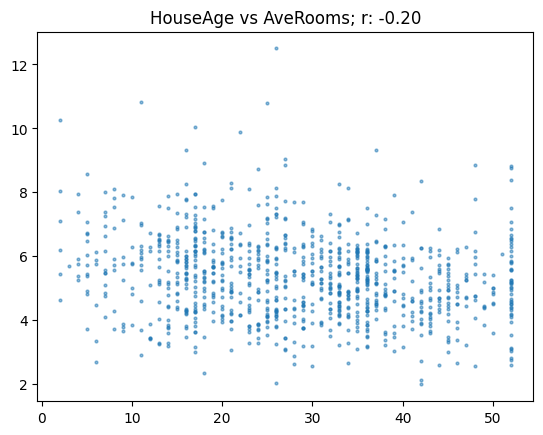
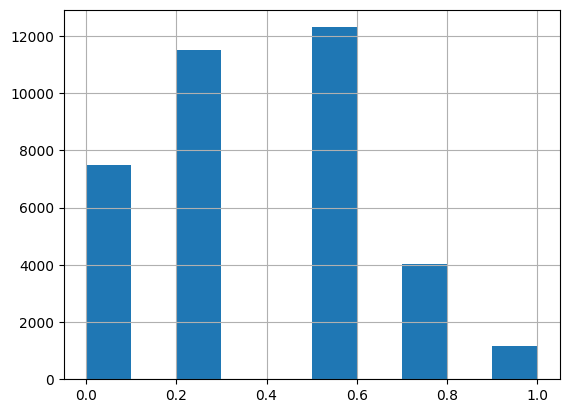
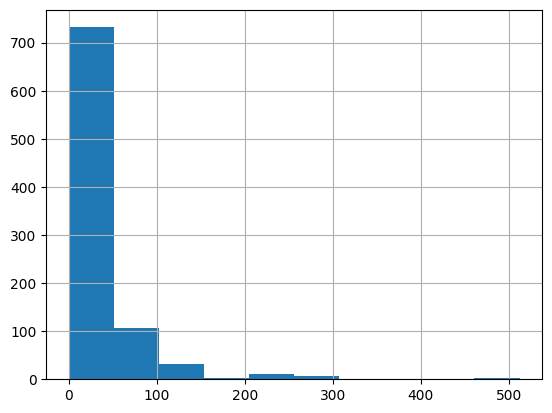
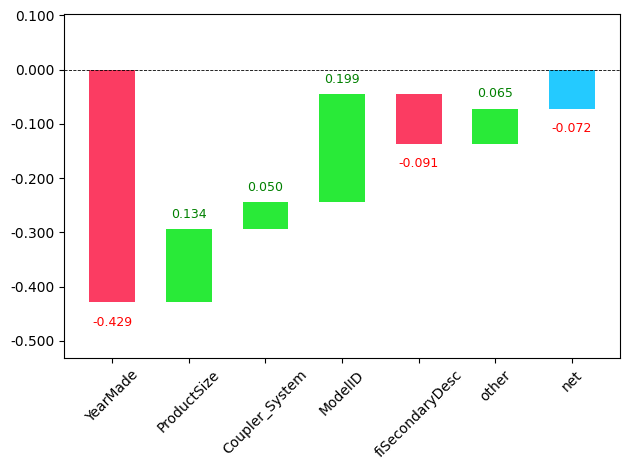
# It's a good idea to ensure you're running the latest version of any libraries you need.
# `!pip install -Uqq <libraries>` upgrades to the latest version of <libraries>
# NB: You can safely ignore any warnings or errors pip spits out about running as root or incompatibilities
!pip install -Uqq fastai fastbook duckduckgo_search timmPractical Deep Learnings For Coders - Part 1 Notes and Examples
Practical Deep Learning for Coders - Part 1
Vishal Bakshi
This notebook contains my notes (of course videos, example notebooks and book chapters) and exercises of Part 1 of the course Practical Deep Learning for Coders.
Lesson 1: Getting Started
Notebook Exercise
The first thing I did was to run through the lesson 1 notebook from start to finish. In this notebook, they download training and validation images of birds and forests then train an image classifier with 100% accuracy in identifying images of birds.
The first exercise is for us to create our own image classifier with our own image searches. I’ll create a classifier which accurately predicts an image of an alligator.
I’ll start by using their example code for getting images using DuckDuckGo image search:
from duckduckgo_search import ddg_images
from fastcore.all import *
def search_images(term, max_images=30):
print(f"Searching for '{term}'")
return L(ddg_images(term, max_results=max_images)).itemgot('image')The search_images function takes a search term and max_images maximum number of images value. It prints out a line of text that it’s "Searching for" the term and returns an L object with the image URL.
The ddg_images function returns a list of JSON objects containing the title, image URL, thumbnail URL, height, width and source of the image.
search_object = ddg_images('alligator', max_results=1)
search_object/usr/local/lib/python3.9/dist-packages/duckduckgo_search/compat.py:60: UserWarning: ddg_images is deprecated. Use DDGS().images() generator
warnings.warn("ddg_images is deprecated. Use DDGS().images() generator")
/usr/local/lib/python3.9/dist-packages/duckduckgo_search/compat.py:64: UserWarning: parameter page is deprecated
warnings.warn("parameter page is deprecated")
/usr/local/lib/python3.9/dist-packages/duckduckgo_search/compat.py:66: UserWarning: parameter max_results is deprecated
warnings.warn("parameter max_results is deprecated")[{'title': 'The Creature Feature: 10 Fun Facts About the American Alligator | WIRED',
'image': 'https://www.wired.com/wp-content/uploads/2015/03/Gator-2.jpg',
'thumbnail': 'https://tse4.mm.bing.net/th?id=OIP.FS96VErnOXAGSWU092I_DQHaE8&pid=Api',
'url': 'https://www.wired.com/2015/03/creature-feature-10-fun-facts-american-alligator/',
'height': 3456,
'width': 5184,
'source': 'Bing'}]Wrapping this list in L object and calling .itemgot('image') on it extracts URL value associated with the image key in the JSON object.
L(search_object).itemgot('image')(#1) ['https://www.wired.com/wp-content/uploads/2015/03/Gator-2.jpg']Next, they provide some code to download the image to a destination filename and view the image:
urls = search_images('alligator', max_images=1)
from fastdownload import download_url
dest = 'alligator.jpg'
download_url(urls[0], dest, show_progress=False)
from fastai.vision.all import *
im = Image.open(dest)
im.to_thumb(256,256)Searching for 'alligator'For my not-alligator images, I’ll use images of a swamp.
download_url(search_images('swamp photos', max_images=1)[0], 'swamp.jpg', show_progress=False)
Image.open('swamp.jpg').to_thumb(256,256)Searching for 'swamp photos'/usr/local/lib/python3.9/dist-packages/duckduckgo_search/compat.py:60: UserWarning: ddg_images is deprecated. Use DDGS().images() generator
warnings.warn("ddg_images is deprecated. Use DDGS().images() generator")
/usr/local/lib/python3.9/dist-packages/duckduckgo_search/compat.py:64: UserWarning: parameter page is deprecated
warnings.warn("parameter page is deprecated")
/usr/local/lib/python3.9/dist-packages/duckduckgo_search/compat.py:66: UserWarning: parameter max_results is deprecated
warnings.warn("parameter max_results is deprecated")In the following code, I’ll search for both terms, alligator and swamp and store the images in alligator_or_not/alligator and alligator_or_not/swamp paths, respectively.
The parents=TRUE argument creates any intermediate parent directories that don’t exist (in this case, the alligator_or_not directory). The exist_ok=TRUE argument suppresses the FileExistsError and does nothing.
searches = 'swamp','alligator'
path = Path('alligator_or_not')
from time import sleep
for o in searches:
dest = (path/o)
dest.mkdir(exist_ok=True, parents=True)
download_images(dest, urls=search_images(f'{o} photo'))
sleep(10) # Pause between searches to avoid over-loading server
download_images(dest, urls=search_images(f'{o} sun photo'))
sleep(10)
download_images(dest, urls=search_images(f'{o} shade photo'))
sleep(10)
resize_images(path/o, max_size=400, dest=path/o)Searching for 'swamp photo'
Searching for 'swamp sun photo'
Searching for 'swamp shade photo'
Searching for 'alligator photo'
Searching for 'alligator sun photo'
Searching for 'alligator shade photo'Next, I’ll train my model using the code they have provided.
The get_image_files function is a fastai function which takes a Path object and returns an L object with paths to the image files.
type(get_image_files(path))fastcore.foundation.Lget_image_files(path)(#349) [Path('alligator_or_not/swamp/1b3c3a61-0f7f-4dc2-a704-38202d593207.jpg'),Path('alligator_or_not/swamp/9c9141f2-024c-4e26-b343-c1ca1672fde8.jpeg'),Path('alligator_or_not/swamp/1340dd85-5d98-428e-a861-d522c786c3d7.jpg'),Path('alligator_or_not/swamp/2d3f91dc-cc5f-499b-bec6-7fa0e938fb13.jpg'),Path('alligator_or_not/swamp/84afd585-ce46-4016-9a09-bd861a5615db.jpg'),Path('alligator_or_not/swamp/6222f0b6-1f5f-43ec-b561-8e5763a91c61.jpg'),Path('alligator_or_not/swamp/a71c8dcb-7bbb-4dba-8ae6-8a780d5c27c6.jpg'),Path('alligator_or_not/swamp/bbd1a832-a901-4e8f-8724-feac35fa8dcb.jpg'),Path('alligator_or_not/swamp/45b358b3-1a12-41d4-8972-8fa98b2baa52.jpg'),Path('alligator_or_not/swamp/cf664509-8eb6-42c8-9177-c17f48bc026b.jpg')...]The fastai parent_label function takes a Path object and returns a string of the file’s parent folder name.
parent_label(Path('alligator_or_not/swamp/18b55d4f-3d3b-4013-822b-724489a23f01.jpg'))'swamp'Some image files that are downloaded may be corrupted, so they have provided a verify_images function to find images that can’t be opened. Those images are then removed (unlinked) from the path.
failed = verify_images(get_image_files(path))
failed.map(Path.unlink)
len(failed)1failed(#1) [Path('alligator_or_not/alligator/1eb55508-274b-4e23-a6ae-dbbf1943a9d1.jpg')]dls = DataBlock(
blocks=(ImageBlock, CategoryBlock),
get_items=get_image_files,
splitter=RandomSplitter(valid_pct=0.2, seed=42),
get_y=parent_label,
item_tfms=[Resize(192, method='squish')]
).dataloaders(path, bs=32)
dls.show_batch(max_n=6)I’ll train the model using their code which uses the resnet18 image classification model, and fine_tunes it for 3 epochs.
learn = vision_learner(dls, resnet18, metrics=error_rate)
learn.fine_tune(3)/usr/local/lib/python3.9/dist-packages/torchvision/models/_utils.py:208: UserWarning: The parameter 'pretrained' is deprecated since 0.13 and will be removed in 0.15, please use 'weights' instead.
warnings.warn(
/usr/local/lib/python3.9/dist-packages/torchvision/models/_utils.py:223: UserWarning: Arguments other than a weight enum or `None` for 'weights' are deprecated since 0.13 and will be removed in 0.15. The current behavior is equivalent to passing `weights=ResNet18_Weights.IMAGENET1K_V1`. You can also use `weights=ResNet18_Weights.DEFAULT` to get the most up-to-date weights.
warnings.warn(msg)
Downloading: "https://download.pytorch.org/models/resnet18-f37072fd.pth" to /root/.cache/torch/hub/checkpoints/resnet18-f37072fd.pth| epoch | train_loss | valid_loss | error_rate | time |
|---|---|---|---|---|
| 0 | 0.690250 | 0.171598 | 0.043478 | 00:03 |
| epoch | train_loss | valid_loss | error_rate | time |
|---|---|---|---|---|
| 0 | 0.127188 | 0.001747 | 0.000000 | 00:02 |
| 1 | 0.067970 | 0.006409 | 0.000000 | 00:02 |
| 2 | 0.056453 | 0.004981 | 0.000000 | 00:02 |
The accuracy is 100%.
Next, I’ll test the model as they’ve done in the lesson.
is_alligator,_,probs = learn.predict(PILImage.create('alligator.jpg'))
print(f"This is an: {is_alligator}.")
print(f"Probability it's an alligator: {probs[0]:.4f}")This is an: alligator.
Probability it's an alligator: 1.0000Video Notes
In this section, I’ll take notes while I watch the lesson 1 video.
- This is the fifth version of the course!
- What seemed impossible in 2015 (image recognition of a bird) is now free and something we can build in 2 minutes.
- All models need numbers as their inputs. Images are already stored as numbers in computers. [PixSpy] allows you to (among other things) view the color of each pixel in an image file.
- A
DataBlockgives fastai all the information it needs to create a computer vision model. - Creating really interesting, real, working programs with deep learning is something that doesn’t take a lot of code, math, or more than a laptop computer. It’s pretty accessible.
- Deep Learning models are doing things that very few, if any of us, believed would be possible to do by computers in our lifetime.
- See the Practical Data Ethics course as well.
- Meta Learning: How To Learn Deep Learning And Thrive In The Digital World.
- Books on learning/education:
- Mathematician’s Lament by Paul Lockhart
- Making Learning Whole by David Perkins
- Why are we able to create a bird-recognizer in a minute or two? And why couldn’t we do it before?
- 2012: Project looking at 5-year survival of breast cancer patients, pre-deep learning approach
- Assembled a team to build ideas for thousands of features that required a lot of expertise, took years.
- They fed these features into a logistic regression model to predict survival.
- Neural networks don’t require us to build these features, they build them for us.
- 2015: Matthew D. Zeiler and Rob Fergus looked inside a neural network to see what it had learned.
- We don’t give it features, we ask it to learn features.
- The neural net is the basic function used in deep learning.
- You start with a random neural network, feed it examples and you have it learn to recognize things.
- The deeper you get, the more sophisticated the features it can find are.
- What we’re going to learn is how neural networks do this automatically.
- This is the key difference in why we can now do things that we couldn’t previously conceive of as possible.
- 2012: Project looking at 5-year survival of breast cancer patients, pre-deep learning approach
- An image recognizer can also be used to classify sounds (pictures of waveforms).
- Turning time series into pictures for image classification.
- fastai is built on top of PyTorch.
!pip install -Uqq fastaito update.- Always view your data at every step of building a model.
- For computer vision algorithms you don’t need particularly big images.
- For big images, most of the time is taken up opening it, the neural net on the GPU is must faster.
- The main thing you’re going to try and figure out is how do I get this data into my model?
DataBlockblocks=(ImageBlock, CategoryBlock):ImageBlockis the type of input to the model,CategoryBlockis the type of model outputget_image_files(path)returns a list of all image files in apath.- It’s critical that you put aside some data for testing the accuracy of your model (validation set) with something like
RandomSplitterfor thesplitterparameter. get_ytells fastai how to get the correct label for the photo.- Most computer vision architectures need all of your inputs to be the same size, using
Resize(eithercropout a piece in the middle orsquishthe image) for the parameteritem_tfms. DataLoaderscontains iterators that PyTorch can run through to grab batches of your data to feed the training algorithm.show_batchshows you a batch of input/label pairs.- A
Learnercombines a model (the actual neural network that we are training) and the data we use to train it with. - PyTorch Image Models (timm).
- resnet has already been trained to recognize over 1 million images of over 1000 different types. fastai downloads this so you can start with a neural network that can do a lot.
fine_tunetakes those pretrained weights downloaded for you and adjusts them in a carefully controlled way to teach the model differences between your dataset and what it was originally trained for.- You pass
.predictan image, which is how you would deploy your model, returns whether it’s a bird or not as a string, integer and probability of whether it’s a bird (in this example).
In the code blocks below, I’ll train the different types of models presented in the video lesson.
Image Segmentation
from fastai.vision.all import *
path = untar_data(URLs.CAMVID_TINY)
dls = SegmentationDataLoaders.from_label_func(
path, bs = 8, fnames = get_image_files(path/"images"),
label_func = lambda o: path/'labels'/f'{o.stem}_P{o.suffix}',
codes = np.loadtxt(path/'codes.txt', dtype=str)
)
learn = unet_learner(dls, resnet34)
learn.fine_tune(8)/usr/local/lib/python3.9/dist-packages/torchvision/models/_utils.py:208: UserWarning: The parameter 'pretrained' is deprecated since 0.13 and will be removed in 0.15, please use 'weights' instead.
warnings.warn(
/usr/local/lib/python3.9/dist-packages/torchvision/models/_utils.py:223: UserWarning: Arguments other than a weight enum or `None` for 'weights' are deprecated since 0.13 and will be removed in 0.15. The current behavior is equivalent to passing `weights=ResNet34_Weights.IMAGENET1K_V1`. You can also use `weights=ResNet34_Weights.DEFAULT` to get the most up-to-date weights.
warnings.warn(msg)
Downloading: "https://download.pytorch.org/models/resnet34-b627a593.pth" to /root/.cache/torch/hub/checkpoints/resnet34-b627a593.pth| epoch | train_loss | valid_loss | time |
|---|---|---|---|
| 0 | 3.454409 | 3.015761 | 00:06 |
| epoch | train_loss | valid_loss | time |
|---|---|---|---|
| 0 | 1.928762 | 1.719756 | 00:02 |
| 1 | 1.649520 | 1.394089 | 00:02 |
| 2 | 1.533350 | 1.344445 | 00:02 |
| 3 | 1.414438 | 1.279674 | 00:02 |
| 4 | 1.291168 | 1.063977 | 00:02 |
| 5 | 1.174492 | 0.980055 | 00:02 |
| 6 | 1.073124 | 0.931532 | 00:02 |
| 7 | 0.992161 | 0.922516 | 00:02 |
It’s amazing how many it’s getting correct because this model was trained in about 24 seconds using a tiny amount of data.
I’ll take a look at the codes out of curiousity, which is an array of string elements describing different objects in view.
np.loadtxt(path/'codes.txt', dtype=str)array(['Animal', 'Archway', 'Bicyclist', 'Bridge', 'Building', 'Car',
'CartLuggagePram', 'Child', 'Column_Pole', 'Fence', 'LaneMkgsDriv',
'LaneMkgsNonDriv', 'Misc_Text', 'MotorcycleScooter', 'OtherMoving',
'ParkingBlock', 'Pedestrian', 'Road', 'RoadShoulder', 'Sidewalk',
'SignSymbol', 'Sky', 'SUVPickupTruck', 'TrafficCone',
'TrafficLight', 'Train', 'Tree', 'Truck_Bus', 'Tunnel',
'VegetationMisc', 'Void', 'Wall'], dtype='<U17')Tabular Analysis
from fastai.tabular.all import *
path = untar_data(URLs.ADULT_SAMPLE)
dls = TabularDataLoaders.from_csv(path/'adult.csv', path=path, y_names='salary',
cat_names = ['workclass', 'education', 'marital-status', 'occupation',
'relationship', 'race'],
cont_names = ['age', 'fnlwgt', 'education-num'],
procs = [Categorify, FillMissing, Normalize])
dls.show_batch()| workclass | education | marital-status | occupation | relationship | race | education-num_na | age | fnlwgt | education-num | salary | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | State-gov | Some-college | Divorced | Adm-clerical | Own-child | White | False | 42.0 | 138162.000499 | 10.0 | <50k |
| 1 | Private | HS-grad | Married-civ-spouse | Other-service | Husband | Asian-Pac-Islander | False | 40.0 | 73025.003080 | 9.0 | <50k |
| 2 | Private | Assoc-voc | Married-civ-spouse | Prof-specialty | Wife | White | False | 36.0 | 163396.000571 | 11.0 | >=50k |
| 3 | Private | HS-grad | Never-married | Sales | Own-child | White | False | 18.0 | 110141.999831 | 9.0 | <50k |
| 4 | Self-emp-not-inc | 12th | Divorced | Other-service | Unmarried | White | False | 28.0 | 33035.002716 | 8.0 | <50k |
| 5 | ? | 7th-8th | Separated | ? | Own-child | White | False | 50.0 | 346013.994175 | 4.0 | <50k |
| 6 | Self-emp-inc | HS-grad | Never-married | Farming-fishing | Not-in-family | White | False | 36.0 | 37018.999571 | 9.0 | <50k |
| 7 | State-gov | Masters | Married-civ-spouse | Prof-specialty | Husband | White | False | 37.0 | 239409.001471 | 14.0 | >=50k |
| 8 | Self-emp-not-inc | Doctorate | Married-civ-spouse | Prof-specialty | Husband | White | False | 50.0 | 167728.000009 | 16.0 | >=50k |
| 9 | Private | HS-grad | Married-civ-spouse | Tech-support | Husband | White | False | 38.0 | 247111.001513 | 9.0 | >=50k |
For tabular models, there’s not generally going to be a pretrained model that already does something like what you want because every table of data is very different, so generally it doesn’t make too much sense to fine_tune a tabular model.
learn = tabular_learner(dls, metrics=accuracy)
learn.fit_one_cycle(2)| epoch | train_loss | valid_loss | accuracy | time |
|---|---|---|---|---|
| 0 | 0.373780 | 0.365976 | 0.832770 | 00:06 |
| 1 | 0.356514 | 0.358780 | 0.833999 | 00:05 |
Collaborative Filtering
The basis of most recommendation systems.
from fastai.collab import *
path = untar_data(URLs.ML_SAMPLE)
dls = CollabDataLoaders.from_csv(path/'ratings.csv')
dls.show_batch()| userId | movieId | rating | |
|---|---|---|---|
| 0 | 457 | 457 | 3.0 |
| 1 | 407 | 2959 | 5.0 |
| 2 | 294 | 356 | 4.0 |
| 3 | 78 | 356 | 5.0 |
| 4 | 596 | 3578 | 4.5 |
| 5 | 547 | 541 | 3.5 |
| 6 | 105 | 1193 | 4.0 |
| 7 | 176 | 4993 | 4.5 |
| 8 | 430 | 1214 | 4.0 |
| 9 | 607 | 858 | 4.5 |
There’s actually no pretrained collaborative filtering model so we could use fit_one_cycle but fine_tune works here as well.
learn = collab_learner(dls, y_range=(0.5, 5.5))
learn.fine_tune(10)| epoch | train_loss | valid_loss | time |
|---|---|---|---|
| 0 | 1.498450 | 1.417215 | 00:00 |
| epoch | train_loss | valid_loss | time |
|---|---|---|---|
| 0 | 1.375927 | 1.357755 | 00:00 |
| 1 | 1.274781 | 1.176326 | 00:00 |
| 2 | 1.033917 | 0.870168 | 00:00 |
| 3 | 0.810119 | 0.719341 | 00:00 |
| 4 | 0.704180 | 0.679201 | 00:00 |
| 5 | 0.640635 | 0.667121 | 00:00 |
| 6 | 0.623741 | 0.661391 | 00:00 |
| 7 | 0.620811 | 0.657624 | 00:00 |
| 8 | 0.606947 | 0.656678 | 00:00 |
| 9 | 0.605081 | 0.656613 | 00:00 |
learn.show_results()| userId | movieId | rating | rating_pred | |
|---|---|---|---|---|
| 0 | 15.0 | 35.0 | 4.5 | 3.886339 |
| 1 | 68.0 | 64.0 | 5.0 | 3.822170 |
| 2 | 62.0 | 33.0 | 4.0 | 3.088149 |
| 3 | 39.0 | 91.0 | 4.0 | 3.788227 |
| 4 | 37.0 | 7.0 | 5.0 | 4.434169 |
| 5 | 38.0 | 98.0 | 3.5 | 4.380877 |
| 6 | 3.0 | 25.0 | 3.0 | 3.443295 |
| 7 | 23.0 | 13.0 | 2.0 | 3.220192 |
| 8 | 15.0 | 7.0 | 4.0 | 4.306846 |
Note: RISE turnes your notebook into a presentation.
Generally speaking, if it’s something that a human can do reasonably quickly, even an expert human (like look at a Go board and decide if it’s a good board or not) then that’s probably something that deep learning will probably be good at. If it’s something that takes logical thought process over time, particularly if it’s not based on much data, deep learning probably won’t do that well.
The first neural network was built in 1957. The basic ideas have not changed much at all.
What’s going on in these models?
- Arthur Samuel in late 1950s invented Machine Learning.
- Normal program: input -> program -> results.
- Machine Learning model: input and weights (parameters) -> model -> results.
- The model is a mathematical function that takes the input, multiplies them with one set of weights and adds them up, then does that again for a second set of weights, and so forth.
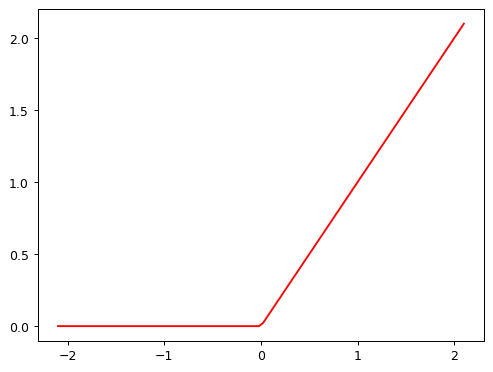
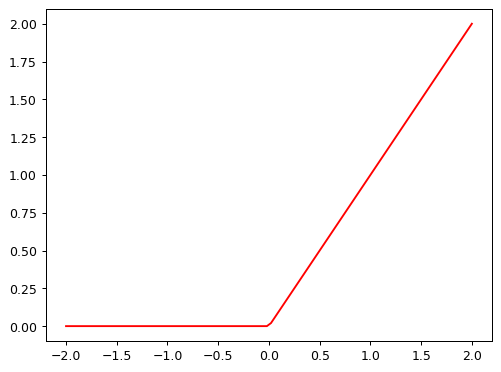
- It takes all of the negative numbers and replaces them with 0.
- It takes all those numbers as inputs to the next layer.
- And it repeats a few times.
- Weights start out as being random.
- A more useful workflow: input/weights -> model -> results -> loss -> update weights.
- The loss is a number that says how good the results were.
- We need a way to come up with a new set of weights that are a bit better than the current weights.
- “bit better” weights means it makes the loss a bit better.
- If we make it a little bit better a few times, it’ll eventually get good.
- Neural nets proven to solve any computable function (i.e. it’s flexible enough to update weights until the results are good).
- “Generate artwork based on someone’s twitter bio” is a computable function.
- Once we’ve finished the training procedure we don’t the loss and the weights can be integrated into the model.
- We end up with inputs -> model -> results which looks like our original idea of a program.
- Deploying a model will have lots of tricky details but there will be one line of code which says
learn.predictwhich takes an input and provides results. - The most important thing to do is experiment.
Book Notes
Chapter 1: Your Deep Learning Journey In this section, I’ll take notes while I read Chapter 1 in the textbook.
Deep Learning is for Everyone
- What you don’t need for deep learning: lots of math, lots of data, lots of expensive computers.
- Deep learning is a computer technique to extract and transform data by using multiple layers of neural networks. Each of these layers takes its inputs from previous layers and progressively refines them. The layers are trained by algorithms that minimize their errors and improve their accuracy. In this way, the network learns to perform a specified task.
Neural Networks: A Brief History
- Warren McCulloch and Walter Pitts developed a mathematical model of an artificial neuron in 1943.
- Most of Pitt’s famous work was done while he was homeless.
- Psychologist Frank Rosenblatt further developed the artificial neuron to give it the ability to learn and built the first device that used these principles, the Mark I Perceptron, which was able to recognize simple shapes.
- Marvin Minsky and Seymour Papert wrote a book about the Perceptron and showed that using multiple layers of the devices would allow the limitations of a single layer to be addressed.
- The 1986 book Parallel Distributed Processing (PDP) by David Rumelhart, James McClelland, and the PDP Research Group defined PDP as requiring the following:
- A set of processing units.
- A state of activation.
- An output function for each unit.
- A pattern of connectivity among units.
- A propogation rule for propagating patterns of activities through the network of connectivities.
- An activation rule for combining the inputs impinging on a unit with the current state of that unit to produce an output for the unit.
- A learning rule whereby patterns of connectivity are modified by experience.
- An environment within which the system must operate.
How to Learn Deep Learning
- The hardest part of deep learning is artisanal: how do you know if you’ve got enough data, whether it is in the right format, if your model is training properly, and, if it’s not, what you should do about it?
from fastai.vision.all import *
path = untar_data(URLs.PETS)/'images'
def is_cat(x): return x[0].isupper()
dls = ImageDataLoaders.from_name_func(
path,
get_image_files(path),
valid_pct=0.2,
seed=42,
label_func=is_cat,
item_tfms=Resize(224)
)
dls.show_batch()learn = cnn_learner(dls, resnet34, metrics=error_rate)
learn.fine_tune(1)/usr/local/lib/python3.10/dist-packages/fastai/vision/learner.py:288: UserWarning: `cnn_learner` has been renamed to `vision_learner` -- please update your code
warn("`cnn_learner` has been renamed to `vision_learner` -- please update your code")
/usr/local/lib/python3.10/dist-packages/torchvision/models/_utils.py:208: UserWarning: The parameter 'pretrained' is deprecated since 0.13 and may be removed in the future, please use 'weights' instead.
warnings.warn(
/usr/local/lib/python3.10/dist-packages/torchvision/models/_utils.py:223: UserWarning: Arguments other than a weight enum or `None` for 'weights' are deprecated since 0.13 and may be removed in the future. The current behavior is equivalent to passing `weights=ResNet34_Weights.IMAGENET1K_V1`. You can also use `weights=ResNet34_Weights.DEFAULT` to get the most up-to-date weights.
warnings.warn(msg)
Downloading: "https://download.pytorch.org/models/resnet34-b627a593.pth" to /root/.cache/torch/hub/checkpoints/resnet34-b627a593.pth
100%|██████████| 83.3M/83.3M [00:00<00:00, 162MB/s]| epoch | train_loss | valid_loss | error_rate | time |
|---|---|---|---|---|
| 0 | 0.140327 | 0.019135 | 0.007442 | 01:05 |
| epoch | train_loss | valid_loss | error_rate | time |
|---|
| epoch | train_loss | valid_loss | error_rate | time |
|---|---|---|---|---|
| 0 | 0.070464 | 0.024966 | 0.006766 | 01:00 |
The error rate is the proportion of images that were incorrectly identified.
Check this model actually works with an image of a dog or cat. I’ll download a picture from google and use it for prediction:
import ipywidgets as widgets
uploader = widgets.FileUpload()
uploaderprint(f'Is this a cat?: {is_cat}.')
print(f"Probability it's a cat: {probs[1].item():.6f}")Is this a cat?: True.
Probability it's a cat: 1.000000What is Machine Learning?
- A traditional program: inputs -> program -> results.
- In 1949, IBM researcher Arthur Samuel started working on machine learning. His basic idea was this: instead of telling the computer the exact steps required to solve a problem, show it examples of the problem to solve, and let it figure out how to solve it itself.
- In 1961 his checkers-playing program had learned so much that it beat the Connecticut state champion.
- Weights are just variables and a weight assignment is a particular choice of values for those variables.
- The program’s inputs are values that it processes in order to produce its results (for instance, taking image pixels as inputs, and returning the classification “dog” as a result).
- Because the weights affect the program, they are in a sense another kind of input.
- A program using weight assignment: inputs and weights -> model -> results.
- A model is a special kind of program, on that can do many different things depending on the weights.
- Weights = parameters, with the term “weights” reserved for a particulat type of model parameter.
- Learning would become entirely automatic when the adjustment of the weights was also automatic.
- Training a maching learning model: inputs and weights -> model -> results -> performance -> update weights.
- results are different than the performance of a model.
- Using a trained model as a program -> inputs -> model -> results.
- maching learning is the training of programs developed by allowing a computer to learn from its experience, rather than through manually coding the individual steps.
What is a Neural Network?
- Neural networks is a mathematical function that can solve any problem to any level of accuracy.
- Stochastic Gradient Descent (SGD) is a completely general way to update the weights of a neural network, to make it improve at any given task.
- Image classification problem:
- Our inputs are the images.
- Our weights are the weights in the neural net.
- Our model is a neural net.
- Our results are the values that are calculated by the neural net, like “dog” or “cat”.
A Bit of Deep Learning Jargon
- The functional form of the model is called its architecture.
- The weights are called parameters.
- The predictions are calculated from the independent variable, which is the data not including the labels.
- The results or the model are called predictions.
- The measure of performance is called the loss.
- The loss depends not only on the predictions, but also on the correct labels (also known as targets or the dependent variable).
- Detailed training loop: inputs and parameters -> architecture -> predictions (+ labels) -> loss -> update parameters.
Limitations Inherent to Machine Learning
- A model cannot be created without data.
- A model can learn to operate on only the patterns seen in the input data used to train it.
- This learning approach creates only predictions, not recommended actions.
- It’s not enough to just have examples of input data, we need labels for that data too.
- Positive feedback loop: the more the model is used, the more biased the data becomes, making the model even more biased, and so forth.
How Our Image Recognizer Works
item_tfmsare applied to each item whilebatch_tfmsare applied to a batch of items at a time using the GPU.- A classification model attempts to predict a class, or category.
- A regression model is one that attempts to predict one or more numeric quantities, such as temperature or location.
- The parameter
seed=42sets the random seed to the same value every time we run this code, which means we get the same validation set every time we run it. This way, if we change our model and retrain it, we know that any differences are due to the changes to the model, not due to having a different random validation set. - We care about how well our model works on previously unseen images.
- The longer you train for, the better your accuracy will get on the training set; the validation set accuracy will also improve for a while, but eventually it will start getting worse as the model starts to memorize the training set rather than finding generalizable underlying patterns in the data. When this happens, we say that the model is overfitting.
- Overfitting is the single most important and challenging issue when training for all machine learning practitioners, and all algorithms.
- You should only use methods to avoid overfitting after you have confirmed that overfitting is occurring (i.e., if you have observed the validation accuracy getting worse during training)
- fastai defaults to
valid_pct=0.2. - Models using architectures with more layers take longer to train and are more prone to overfitting, on the other hand, when using more data, they can be quite a bit more accurate.
- A metric is a function that measures the quality of the model’s predictions using the validation set.
- error_rate tells you what percentage of inputs in the validation set are being classified incorrectly.
- accuracy =
1.0 - error_rate. - The entire purpose of loss is to define a “measure of performance” that the training system can use to update weights automatically. A good choice for loss is a choice that is easy for stochastic gradient descent to use. But a metric is defined for human consumption, so a good metric is one that is easy for you to understand.
- A model that has weights that have already been trained on another dataset is called a pretrained model.
- When using a pretrained model,
cnn_learnerwill remove the last layer and replace it with one or more new layers with randomized weights. This last part of the model is known as the head. - Using a pretrained model for a task different from what is was originally trained for is known as transfer learning.
- The architecture only describes a template for a mathematical function; it doesn’t actually do anything until we provide values for the millions of parameters it contains.
- To fit a model, we have to provide at least one piece of information: how many times to look at each image (known as number of epochs).
fitwill fit a model (i.e., look at images in the training set multiple times, each time updating the parameters to make the predictions closer and closer to the target labels).- Fine-Tuning: a transfer learning technique that updates the parameters of a pretrained model by training for additional epochs using a different task from that used for pretraining.
fine_tunehas a few parameters you can set, but in the default form it does two steps:- Use one epoch to fit just those parts of the model necessary to get the new random head to work correctly with your dataset.
- Use the number of epochs requested when calling the method to fit the entire model, updating the weights of the later layers (especially the head) faster than the earlier layers (which don’t require many changes from the pretrained weights).
- The head of the model is the part that is newly added to be specific to the new dataset.
- An epoch is one complete pass through the dataset.
What Our Image Recognizer Learned
- When we fine tune our pretrained models, we adapt what the last layers focus on to specialize on the problem at hand.
Image Recognizers Can Tackle Non-Image Tasks
- A lot of things can be represented as images.
- Sound can be converted to a spectogram.
- Times series data can be created into an image using Gramian Angular Difference Field (GADF).
- If the human eye can recognize categories from the images, then a deep learning model should be able to do so too.
Jargon Recap
| Term | Meaning |
|---|---|
| Label | The data that we’re trying to predict |
| Architecture | The template of the model that we’re trying to fit; i.e., the actual mathematical function that we’re passing the input data and parameters to |
| Model | The combination of the architecture with a particular set of parameters |
| Parameters | The values in the model that change what task it can do and that are updated through model training |
| Fit | Update the parameters of the model such that the predictions of the model using the input data match the target labels |
| Train | A synonym for fit |
| Pretrained Model | A model that has already been trained, generally using a large dataset, and will be fine-tuned |
| Fine-tune | Update a pretrained model for a different task |
| Epoch | One complete pass through the input data |
| Loss | A measure of how good the model is, chosen to drive training via SGD |
| Metric | A measurement of how good the model is using the validation set, chosen for human consumption |
| Validation set | A set of data held out from training, used only for measuring how good the model is |
| Training set | The data used for fitting the model; does not include any data from the validation set |
| Overfitting | Training a model in such a way that it remembers specific features of the input data, rather than generalizing wel to data not seen during training |
| CNN | Convolutional neural network; a type of neural network that works particularly well for computer vision tasks |
Deep Learning is Not Just for Image Classification
- Segmentation
- Natural language processing (see below)
- Tabular (see Adults income classification above)
- Collaborative filtering (see MovieLens ratings predictor above)
- Start by using one of the cut-down dataset versions and later scale up to the full-size version. This is how the world’s top practitioners do their modeling in practice; they do most of their experimentation and prototyping with subsets of their data, and use the full dataset only when they have a good understanding of what they have to do.
Validation Sets and Test Sets
- If the model makes an accurate prediction for a data item, that should be because it has learned characteristics of that kind of item, and not because the model has been shaped by actually having seen that particular item.
- Hyperparameters: various modeling choices regarding network architecture, learning rates, data augmentation strategies, and other factors.
- We, as modelers, are evaluating the model by looking at predictions on the validation data when we decide to explore new hyperparameter values and we are in danger of overfitting the validation data through human trial and error and exploration.
- The test set can be used only to evaluate the model at the very end of our efforts.
- Training data is fully exposed to training and modeling processes, validation data is less exposed and test data is fully hidden.
- The test and validation sets should have enough data to ensure that you get a good estimate of your accuracy.
- The discipline of the test set helps us keep ourselves intellectually honest.
- It’s a good idea for you to try out a simple baseline model yourself, so you know what a really simply model can achieve.
Use Judgment in Defining Test Sets
- A key property of the validation and test sets is that they must be representative of the new data you will see in the future.
- As an example, for time series data, use earlier dates for training set and later more recent dates as validation set
- The data you will be making predictions for in production may be qualitatively different from the data you have to train your model with.
from fastai.text.all import *
# I'm using IMDB_SAMPLE instead of the full IMDB dataset since it either takes too long or
# I get a CUDA Out of Memory error if the batch size is more than 16 for the full dataset
# Using a batch size of 16 with the sample dataset works fast
dls = TextDataLoaders.from_csv(
path=untar_data(URLs.IMDB_SAMPLE),
csv_fname='texts.csv',
text_col=1,
label_col=0,
bs=16)
dls.show_batch()| text | category | |
|---|---|---|
| 0 | xxbos xxmaj raising xxmaj victor xxmaj vargas : a xxmaj review \n\n xxmaj you know , xxmaj raising xxmaj victor xxmaj vargas is like sticking your hands into a big , xxunk bowl of xxunk . xxmaj it 's warm and gooey , but you 're not sure if it feels right . xxmaj try as i might , no matter how warm and gooey xxmaj raising xxmaj victor xxmaj vargas became i was always aware that something did n't quite feel right . xxmaj victor xxmaj vargas suffers from a certain xxunk on the director 's part . xxmaj apparently , the director thought that the ethnic backdrop of a xxmaj latino family on the lower east side , and an xxunk storyline would make the film critic proof . xxmaj he was right , but it did n't fool me . xxmaj raising xxmaj victor xxmaj vargas is | negative |
| 1 | xxbos xxup the xxup shop xxup around xxup the xxup corner is one of the xxunk and most feel - good romantic comedies ever made . xxmaj there 's just no getting around that , and it 's hard to actually put one 's feeling for this film into words . xxmaj it 's not one of those films that tries too hard , nor does it come up with the xxunk possible scenarios to get the two protagonists together in the end . xxmaj in fact , all its charm is xxunk , contained within the characters and the setting and the plot … which is highly believable to xxunk . xxmaj it 's easy to think that such a love story , as beautiful as any other ever told , * could * happen to you … a feeling you do n't often get from other romantic comedies | positive |
| 2 | xxbos xxmaj now that xxmaj che(2008 ) has finished its relatively short xxmaj australian cinema run ( extremely limited xxunk screen in xxmaj xxunk , after xxunk ) , i can xxunk join both xxunk of " at xxmaj the xxmaj movies " in taking xxmaj steven xxmaj soderbergh to task . \n\n xxmaj it 's usually satisfying to watch a film director change his style / subject , but xxmaj soderbergh 's most recent stinker , xxmaj the xxmaj girlfriend xxmaj xxunk ) , was also missing a story , so narrative ( and editing ? ) seem to suddenly be xxmaj soderbergh 's main challenge . xxmaj strange , after 20 - odd years in the business . xxmaj he was probably never much good at narrative , just xxunk it well inside " edgy " projects . \n\n xxmaj none of this excuses him this present , | negative |
| 3 | xxbos i really wanted to love this show . i truly , honestly did . \n\n xxmaj for the first time , gay viewers get their own version of the " the xxmaj bachelor " . xxmaj with the help of his obligatory " hag " xxmaj xxunk , xxmaj james , a good looking , well - to - do thirty - something has the chance of love with 15 suitors ( or " mates " as they are referred to in the show ) . xxmaj the only problem is half of them are straight and xxmaj james does n't know this . xxmaj if xxmaj james picks a gay one , they get a trip to xxmaj new xxmaj zealand , and xxmaj if he picks a straight one , straight guy gets $ 25 , xxrep 3 0 . xxmaj how can this not be fun | negative |
| 4 | xxbos xxmaj many neglect that this is n't just a classic due to the fact that it 's the first 3d game , or even the first xxunk - up . xxmaj it 's also one of the first xxunk games , one of the xxunk definitely the first ) truly claustrophobic games , and just a pretty well - xxunk gaming experience in general . xxmaj with graphics that are terribly dated today , the game xxunk you into the role of xxunk even * think * xxmaj i 'm going to attempt spelling his last name ! ) , an xxmaj american xxup xxunk . caught in an underground bunker . xxmaj you fight and search your way through xxunk in order to achieve different xxunk for the six xxunk , let 's face it , most of them are just an excuse to hand you a weapon | positive |
| 5 | xxbos xxmaj i 'm sure things did n't exactly go the same way in the real life of xxmaj homer xxmaj hickam as they did in the film adaptation of his book , xxmaj rocket xxmaj boys , but the movie " october xxmaj sky " ( an xxunk of the book 's title ) is good enough to stand alone . i have not read xxmaj hickam 's memoirs , but i am still able to enjoy and understand their film adaptation . xxmaj the film , directed by xxmaj joe xxmaj xxunk and written by xxmaj lewis xxmaj xxunk , xxunk the story of teenager xxmaj homer xxmaj hickam ( jake xxmaj xxunk ) , beginning in xxmaj october of 1957 . xxmaj it opens with the sound of a radio broadcast , bringing news of the xxmaj russian satellite xxmaj xxunk , the first artificial satellite in | positive |
| 6 | xxbos xxmaj to review this movie , i without any doubt would have to quote that memorable scene in xxmaj tarantino 's " pulp xxmaj fiction " ( xxunk ) when xxmaj jules and xxmaj vincent are talking about xxmaj mia xxmaj wallace and what she does for a living . xxmaj jules tells xxmaj vincent that the " only thing she did worthwhile was pilot " . xxmaj vincent asks " what the hell is a pilot ? " and xxmaj jules goes into a very well description of what a xxup tv pilot is : " well , the way they make shows is , they make one show . xxmaj that show 's called a ' pilot ' . xxmaj then they show that show to the people who make shows , and on the strength of that one show they decide if they 're going to | negative |
| 7 | xxbos xxmaj how viewers react to this new " adaption " of xxmaj shirley xxmaj jackson 's book , which was promoted as xxup not being a remake of the original 1963 movie ( true enough ) , will be based , i suspect , on the following : those who were big fans of either the book or original movie are not going to think much of this one … and those who have never been exposed to either , and who are big fans of xxmaj hollywood 's current trend towards " special effects " being the first and last word in how " good " a film is , are going to love it . \n\n xxmaj things i did not like about this adaption : \n\n 1 . xxmaj it was xxup not a true adaption of the book . xxmaj from the xxunk i had | negative |
| 8 | xxbos xxmaj the trouble with the book , " memoirs of a xxmaj geisha " is that it had xxmaj japanese xxunk but underneath the xxunk it was all an xxmaj american man 's way of thinking . xxmaj reading the book is like watching a magnificent ballet with great music , sets , and costumes yet performed by xxunk animals dressed in those xxunk far from xxmaj japanese ways of thinking were the characters . \n\n xxmaj the movie is n't about xxmaj japan or real geisha . xxmaj it is a story about a few xxmaj american men 's mistaken ideas about xxmaj japan and geisha xxunk through their own ignorance and misconceptions . xxmaj so what is this movie if it is n't about xxmaj japan or geisha ? xxmaj is it pure fantasy as so many people have said ? xxmaj yes , but then why | negative |
learn = text_classifier_learner(dls, AWD_LSTM, drop_mult=0.5, metrics=accuracy)
learn.fine_tune(4, 1e-2)| epoch | train_loss | valid_loss | accuracy | time |
|---|---|---|---|---|
| 0 | 0.629276 | 0.553454 | 0.740000 | 00:19 |
| epoch | train_loss | valid_loss | accuracy | time |
|---|---|---|---|---|
| 0 | 0.466581 | 0.548400 | 0.740000 | 00:30 |
| 1 | 0.410401 | 0.418941 | 0.825000 | 00:30 |
| 2 | 0.286162 | 0.410872 | 0.830000 | 00:31 |
| 3 | 0.192047 | 0.405275 | 0.845000 | 00:31 |
# view actual vs prediction
learn.show_results()| text | category | category_ | |
|---|---|---|---|
| 0 | xxbos xxmaj this film sat on my xxmaj xxunk for weeks before i watched it . i xxunk a self - indulgent xxunk flick about relationships gone bad . i was wrong ; this was an xxunk xxunk into the screwed - up xxunk of xxmaj new xxmaj xxunk . \n\n xxmaj the format is the same as xxmaj max xxmaj xxunk ' " la xxmaj xxunk , " based on a play by xxmaj arthur xxmaj xxunk , who is given an " inspired by " credit . xxmaj it starts from one person , a prostitute , standing on a street corner in xxmaj brooklyn . xxmaj she is picked up by a home contractor , who has sex with her on the hood of a car , but ca n't come . xxmaj he refuses to pay her . xxmaj when he 's off xxunk , she | positive | positive |
| 1 | xxbos xxmaj bonanza had a great cast of wonderful actors . xxmaj xxunk xxmaj xxunk , xxmaj pernell xxmaj whitaker , xxmaj michael xxmaj xxunk , xxmaj dan xxmaj blocker , and even xxmaj guy xxmaj williams ( as the cousin who was brought in for several episodes during 1964 to replace xxmaj adam when he was leaving the series ) . xxmaj the cast had chemistry , and they seemed to genuinely like each other . xxmaj that made many of their weakest stories work a lot better than they should have . xxmaj it also made many of their best stories into great western drama . \n\n xxmaj like any show that was shooting over thirty episodes every season , there are bound to be some weak ones . xxmaj however , most of the time each episode had an interesting story , some kind of conflict , | positive | negative |
| 2 | xxbos i watched xxmaj grendel the other night and am compelled to put together a xxmaj public xxmaj service xxmaj announcement . \n\n xxmaj grendel is another version of xxmaj beowulf , the thousand - year - old xxunk - saxon epic poem . xxmaj the scifi channel has a growing catalog of xxunk and uninteresting movies , and the previews promised an xxunk low - budget mini - epic , but this one xxunk to let me switch xxunk . xxmaj it was xxunk , xxunk , bad . i watched in xxunk and horror at the train wreck you could n't tear your eyes away from . i reached for a xxunk and managed to capture part of what i was seeing . xxmaj the following may contain spoilers or might just save your xxunk . xxmaj you 've been warned . \n\n - xxmaj just to get | negative | negative |
| 3 | xxbos xxmaj this is the last of four xxunk from xxmaj france xxmaj i 've xxunk for viewing during this xxmaj christmas season : the others ( in order of viewing ) were the uninspired xxup the xxup black xxup tulip ( 1964 ; from the same director as this one but not nearly as good ) , the surprisingly effective xxup lady xxmaj oscar ( 1979 ; which had xxunk as a xxmaj japanese manga ! ) and the splendid xxup cartouche ( xxunk ) . xxmaj actually , i had watched this one not too long ago on late - night xxmaj italian xxup tv and recall not being especially xxunk over by it , so that i was genuinely surprised by how much i enjoyed it this time around ( also bearing in mind the xxunk lack of enthusiasm shown towards the film here and elsewhere when | positive | positive |
| 4 | xxbos xxmaj this is not really a zombie film , if we 're xxunk zombies as the dead walking around . xxmaj here the protagonist , xxmaj xxunk xxmaj louque ( played by an unbelievably young xxmaj dean xxmaj xxunk ) , xxunk control of a method to create zombies , though in fact , his ' method ' is to mentally project his thoughts and control other living people 's minds turning them into hypnotized slaves . xxmaj this is an interesting concept for a movie , and was done much more effectively by xxmaj xxunk xxmaj lang in his series of ' dr . xxmaj mabuse ' films , including ' dr . xxmaj mabuse the xxmaj xxunk ' ( 1922 ) and ' the xxmaj testament of xxmaj dr . xxmaj mabuse ' ( 1933 ) . xxmaj here it is unfortunately xxunk to his quest to | negative | positive |
| 5 | xxbos " once upon a time there was a charming land called xxmaj france … . xxmaj people lived happily then . xxmaj the women were easy and the men xxunk in their favorite xxunk : war , the only xxunk of xxunk which the people could enjoy . " xxmaj the war in question was the xxmaj seven xxmaj year 's xxmaj war , and when it was noticed that there were more xxunk of soldiers than soldiers , xxunk were sent out to xxunk the ranks . \n\n xxmaj and so it was that xxmaj fanfan ( gerard xxmaj philipe ) , caught xxunk a farmer 's daughter in a pile of hay , escapes marriage by xxunk in the xxmaj xxunk xxunk … but only by first believing his future as xxunk by a gypsy , that he will win fame and fortune in xxmaj his xxmaj | positive | positive |
| 6 | xxbos xxup ok , let me again admit that i have n't seen any other xxmaj xxunk xxmaj ivory ( the xxunk ) films . xxmaj nor have i seen more celebrated works by the director , so my capacity to xxunk xxmaj before the xxmaj rains outside of analysis of the film itself is xxunk . xxmaj with that xxunk , let me begin . \n\n xxmaj before the xxmaj rains is a different kind of movie that does n't know which genre it wants to be . xxmaj at first , it pretends to be a romance . xxmaj in most romances , the protagonist falls in love with a supporting character , is separated from the supporting character , and is ( sometimes ) united with his or her partner . xxmaj this movie 's hero has already won the heart of his lover but can not | negative | negative |
| 7 | xxbos xxmaj first off , anyone looking for meaningful " outcome xxunk " cinema that packs some sort of social message with meaningful performances and soul searching dialog spoken by dedicated , xxunk , heartfelt xxunk , please leave now . xxmaj you are wasting your time and life is short , go see the new xxmaj xxunk xxmaj jolie movie , have a good cry , go out & buy a xxunk car or throw away your conflict xxunk if that will make you feel better , and leave us alone . \n\n xxmaj do n't let the door hit you on the way out either . xxup the xxup incredible xxup melting xxup man is a grade b minus xxunk horror epic shot in the xxunk of xxmaj oklahoma by a young , xxup tv friendly cast & crew , and concerns itself with an astronaut who is | positive | negative |
| 8 | xxbos " national xxmaj treasure " ( 2004 ) is a thoroughly misguided xxunk - xxunk of plot xxunk that borrow from nearly every xxunk and dagger government conspiracy cliché that has ever been written . xxmaj the film stars xxmaj nicholas xxmaj cage as xxmaj benjamin xxmaj xxunk xxmaj xxunk ( how precious is that , i ask you ? ) ; a seemingly normal fellow who , for no other reason than being of a xxunk of like - minded misguided fortune hunters , decides to steal a ' national treasure ' that has been hidden by the xxmaj united xxmaj states xxunk fathers . xxmaj after a bit of subtext and background that plays laughably ( unintentionally ) like xxmaj indiana xxmaj jones meets xxmaj the xxmaj patriot , the film xxunk into one misguided xxunk after another – attempting to create a ' stanley xxmaj xxunk | negative | negative |
review_text = "I really liked the movie!"
learn.predict(review_text)('positive', tensor(1), tensor([0.0174, 0.9826]))Questionnaire
- Do you need these for deep learning?
- Lots of Math (FALSE).
- Lots of Data (FALSE).
- Lots of expensive computers (FALSE).
- A PhD (FALSE).
- Name five areas where deep learning is now the best tool in the world
- Natural Language Processing (NLP).
- Computer vision.
- Medicine.
- Image generation.
- Recommendation systems.
- What was the name of the first device that was based on the principle of the artificial neuron?
- Mark I Perceptron.
- Based on the book of the same name, what are the requirements for parallel distributed processing (PDP)?
- A series of processing units.
- A state of activation.
- An output function for each unit.
- A pattern of connectivity among units.
- A propagation rule for propagating patterns of activities through the network of connectivities.
- An activation rule for combining the inputs impinging on a unit with the current state of that unit to produce an output for the unit.
- A learning rule whereby patterns of connectivity are modified by experience.
- An environment within which the system must operate.
- What were the two theoretical misunderstandings that held back the field of neural networks?
- Using multiple layers of the device would allow limitations of one layer to be addressed—this was ignored.
- More than two layers are needed to get practical, good perforamnce—only in the last decade has this been more widely appreciated and applied.
- What is a GPU?
- A Graphical Processing Unit, which can perform thousands of tasks at the same time.
- Open a notebook and execute a cell containing:
1+1. What happens?- Depending on the server, it may take some time for the output to generate, but running this cell will output
2.
- Depending on the server, it may take some time for the output to generate, but running this cell will output
- Follow through each cell of the stripped version of the notebook for this chapter. Before executing each cell, guess what will happen.
- (I did this for the notebook shared for Lesson 1).
- Complete the Jupyter Notebook online appendix.
- Done. Will reference some of it again.
- Why is it hard to use a traditional computer program to recognize images in a photo?
- Because it’s hard to instruct a computer clear instructions to recognize images.
- What did Samuel mean by “weight assignment”?
- A particular choice for weights (variables)
- What term do we normally use in deep learning for what Samuel called “weights”?
- Parameters
- Draw a picture that summarizes Samuel’s view of a machine learning model
- input and weights -> model -> results -> performance -> update weights/inputs
- Why is it hard to understand why a deep learning model makes a particular prediction?
- Because a deep learning model has many layers and connectivities and activations between neurons that are not intuitive to our understanding.
- What is the name of the theorem that shows that a neural network can solve any mathematical problem to any level of accuracy?
- Universal approximation theorem.
- What do you need in order to train a model?
- Labeled data (Inputs and targets).
- Architecture.
- Initial weights.
- A measure of performance (loss, accuracy).
- A way to update the model (SGD).
- How could a feedback loop impact the rollout of a predictive policing model?
- The model will end up predicting where arrests are made, not where crime is taking place, so more police officers will go to locations where more arrests are predicted and feed that data back to the model which will reinforce the prediction of arrests in those areas, continuing this feedback loop of predictions -> arrests -> predictions.
- Do we always have to use 224x224-pixel images with the cat recognition model?
- No, that’s just the convention for image recognition models.
- You can use larger images but it will slow down the training process (it takes longer to open up bigger images).
- What is the difference between classification and regression?
- Classification predicts discrete classes or categories.
- Regression predicts continuous values.
- What is a validation set? What is a test set? Why do we need them?
- A validation set is a dataset upon which a model’s accuracy (or metrics in general) is calculated during training, as well as the dataset upon which the performance of different hyperparameters (like batch size and learning rate) are measured.
- A test set is a dataset upon which a model’s final performance is measured, a truly unseen dataset for both the model and the practitioner
- What will fastai do if you don’t provide a validation set?
- Set aside a random 20% of the data as the validation set by default
- Can we always use a random sample for a validation set? Why or why not?
- No, in situations where we want to ensure that the model’s accuracy is evaluated on data the model has not seen, we should not use a random validation set. Instead, we should create an intentional validation set. For example:
- For time series data, use the most recent dates as the validation set
- For human recognition data, use images of different people for training and validation sets
- No, in situations where we want to ensure that the model’s accuracy is evaluated on data the model has not seen, we should not use a random validation set. Instead, we should create an intentional validation set. For example:
- What is overfitting? Provide an example.
- Overfitting is when a model memorizes features of the training dataset instead of learning generalizations of the features in the data. An example of this is when a model memorizes training data facial features but then cannot recognize different faces in the real world. Another example is when a model memorizes the handwritten digits in the training data, so it cannot then recognize digits written in different handwriting. Overfitting can be observed during training when the validation loss starts to increase as the training loss decreases.
- What is a metric? How does it differ from loss?
- A metric a measurement of how good a model is performing, chosen for human consumption. A loss is also a measurement of how good a model is performing, but it’s chosen to drive training using an optimizer.
- How can pretrained models help?
- Pretrained models are already good at recognizing many generalized features and so they can help by providing a set of weights in an architecture that are capable, reducing the amount of time you need to train a model specific to your task.
- What is the “head” of the model?
- The last/top few neural network layers which are replaced with randomized weights in order to specialize your model via training on the task at hand (and not the task it was pretrained to perform).
- What kinds of features do the early layers of a CNN find? How about the later layers?
- Early layers: simple features lie lines, color gradients
- Later layers: compelx features like dog faces, outlines of people
- Are image models useful only for photos?
- No! Lots of things can be represented by images so if you can represent something (like a sound) as an image (spectogram) and differences between classes/categories are easily recognizable by the human eye, you can train an image classifier to recognize it.
- What is an architecture?
- A template, mathematical function, to which you pass input data to in order to fit/train a model
- What is segmentation?
- Recognizing different objects in an image based on pixel colors (each object is a different pixel color)
- What is
y_rangeused for? When do we need it?- It’s used to specify the output range of a regression model. We need it when the target is a continuous value.
- What are hyperparameters?
- Modeling choices such as network architecture, learning rates, data augmentation strategies and other higher level choices that govern the meaning of the weight parameters.
- What is the best way to avoid failures when using AI in an organization?
- Making sure you have good validation and test sets to evaluate the performance of a model on real world data.
- Trying out a simple baseline model to know what level of performance such a model can achieve.
Further Research
- Why is a GPU useful for deep learning? How is a CPU different, and why is it less effective for deep learning?
- CPU vs GPU for Machine Learning
- CPUs process tasks in a sequential manner, GPUs process tasks in parallel.
- GPUs can have thousands of cores, processing tasks at the same time.
- GPUs have many cores processing at low speeds, CPUs have few cores processing at high speeds.
- Some algorithms are optimized for CPUs rather than GPUs (time series data, recommendation systems that need lots of memory).
- Neural networks are designed to process tasks in parallel.
- CPU vs GPU in Machine Learning Algorithms: Which is Better?
- Machine Learning Operations Preferred on CPUs
- Recommendation systems that involve huge memory for embedding layers.
- Support vector machines, time-series data, algorithms that don’t require parallel computing.
- Recurrent neural networks because they use sequential data.
- Algorithms with intensive branching.
- Machine Learning Operations Preferred on GPUs
- Operations that involve parallelism.
- Machine Learning Operations Preferred on CPUs
- Why Deep Learning Uses GPUs
- Neural networks are specifically made for running in parallel.
- CPU vs GPU for Machine Learning
- Try to think of three areas where feedback loops might impact the use of machine learning. See if you can find documented examples of that happening in practice.
- Hidden Risks of Machine Learning Applied to Healthcare: Unintended Feedback Loops Between Models and Future Data Causing Model Degradation
- If clinicians fully trust the machine learning model (100% adoption of the predicted label) the false positive rate (FPR) grows uncontrollably with the number of updates.
- Runaway Feedback Loops in Predictive Policing
- Once police are deployed based on these predictions, data from observations in the neighborhood is then used to further update the model.
- Discovered crime data (e.g., arrest counts) are used to help update the model, and the process is repeated.
- Predictive policing systems have been empirically shown to be susceptible to runaway feedback loops, where police are repeatedly sent back to the same neighborhoods regardless of the true crime rate.
- Pitfalls of Predictive Policing: An Ethical Analysis
- Predictive policing relies on a large database of previous crime data and forecasts where crime is likely to occur. Since the program relies on old data, those previous arrests need to be unbiased to generate unbiased forecasts.
- People of color are arrested far more often than white people for committing the same crime.
- Racially biased arrest data creates biased forecasts in neighborhoods where more people of color are arrested.
- If the predictive policing algorithm is using biased data to divert more police forces towards less affluent neighborhoods and neighborhoods of color, then those neighborhoods are not receiving the same treatment as others.
- Bias in Criminal Risk Scores Is Mathematically Inevitable, Researchers Say
- The algorithm COMPAS which predicts whether a person is “high-risk” and deemed more likely to be arrested in the future, leads to being imprisoned (instead of sent to rehab) or longer sentences.
- Can bots discriminate? It’s a big question as companies use AI for hiring
- If an older candidate makes it past the resume screening process but gets confused by or interacts poorly with the chatbot, that data could teach the algorithm that candidates with similar profiles should be ranked lower
- Echo chambers, rabbit holes, and ideological bias: How YouTube recommends content to real users
- We find that YouTube’s algorithm pushes real users into (very) mild ideological echo chambers.
- We found that 14 out of 527 (~3%) of our users ended up in rabbit holes.
- Finally, we found that, regardless of the ideology of the study participant, the algorithm pushes all users in a moderately conservative direction.
- Hidden Risks of Machine Learning Applied to Healthcare: Unintended Feedback Loops Between Models and Future Data Causing Model Degradation
Lesson 2: Deployment
I’m going to do things a bit differently than how I approached Lesson 1. Jeremy suggested that we first watch the video without pausing in order to understand what we’re going to do and then watch it a second time and follow along. I also want to be mindful of how long I’m running my Paperspace Gradient maching (at $0.51/hour) so that I don’t run the machine when I don’t need its GPU.
So, here’s how I’m going to approach Lesson 2: - Read the Chapter 2 Questionnaire so I know what I’ll be “tested” on at the end - Watch the video without taking notes or running code - Rewatch the video and take notes in this notebook - Add the Kaggle code cells to this notebook and run them in Paperspace - Read the Gradio tutorial without running code - Re-read the Gradio tutorial and follow along with my own code - Read Chapter 2 in the textbook and run code in this notebook in Paperspace - Read Chapter 2 in the textbook and take notes in this notebook (including answers to the Questionnaire)
With this approach, I’ll have a big picture understanding of each step of the lesson and I’ll minimize the time I’m spending running my Paperspace Gradient machine.
Video Notes
Link to this lesson’s video.
- In this lesson we’re doing things that hasn’t been in courses like this before.
- Resource: aiquizzes.com—I signed up and answered a couple of questions.
- Don’t forget the FastAI Forums
- Click “Summarize this Topic” to get a list of the most upvoted posts
- How do we go about putting a model in production?
- Figure out what problem you want to solve
- Figure out how to get data for it
- Gather some data
- Use DuckDuckGo image function
- Download data
- Get rid of images that failed to open
- Data cleaning
- Before you clean your data, train the model
ImageClassifierCleanercan be used to clean (delete or re-label) the wrongly labeled data in the dataset- cleaner orders by loss so you only need to look at the first few
- Always build a model to find out what things are difficult to recognize in your data and to find the things the model can help you find that are problems in the data
- Train your model again
- Deploy to HuggingFace Spaces
- Install Jupyter Notebook Extensions to get features like table of contents and collapsible sections (with which you can also navigate sections using arrow keys)
- Type
??followed by function name to get source code - Type
?followed by function name to get brief info - If you have nbdev installed
doc(<fn>)will give you link to documentation - Different ways to resize an image
ResizeMethod.Squish(to see the whole picture with different aspect ratio)ResizeMethod.Pad(whole image in correct aspect ratio)
- Data Augmentation
RandomResizedCrop(different bit of an image everytime)batch_tfms=aug_tranforms()(images get turned, squished, warped, saturated, recolored, etc.)- Use if you are training for more than 5-10 epochs
- In memory, real-time, the image is being resized/cropped/etc.
- Confusion matrix (
ClassificationInterpretation)- Only meaningful for category labels
- Shows what category errors your model is making (actual vs predicted)
- In a lot of situations this will let you know what the hard categories to classify are (e.g. breeds of pets hard to identify)
.plot_top_lossestells us where the loss is the highest (prediction/actual/loss/probability)- A loss will be bad (high) if we are wrong + confident or right + unconfident
- On your computer, normal RAM doesn’t get filled up as it saves RAM to hard disk (swapping). GPUs don’t do swapping so do only one thing at a time so you’re not using up all the memory.
- Gradio + HuggingFace Spaces
- Here is my Hello World HuggingFace Space!
- Next, we’ll put a deep learning model in production. In the code cells below, I will train and export a dog vs cat classifier.
# import all the stuff we need from fastai
from fastai.vision.all import *
from fastbook import *# download and decompress our dataset
path = untar_data(URLs.PETS)/'images'# define a function to label our images
def is_cat(x): return x[0].isupper()# create `DataLoaders`
dls = ImageDataLoaders.from_name_func('.',
get_image_files(path),
valid_pct = 0.2,
seed = 42,
label_func = is_cat,
item_tfms = Resize(192))# train our model using resnet18 to keep it small and fast
learn = vision_learner(dls, resnet18, metrics = error_rate)
learn.fine_tune(3)/usr/local/lib/python3.9/dist-packages/torchvision/models/_utils.py:208: UserWarning: The parameter 'pretrained' is deprecated since 0.13 and will be removed in 0.15, please use 'weights' instead.
warnings.warn(
/usr/local/lib/python3.9/dist-packages/torchvision/models/_utils.py:223: UserWarning: Arguments other than a weight enum or `None` for 'weights' are deprecated since 0.13 and will be removed in 0.15. The current behavior is equivalent to passing `weights=ResNet18_Weights.IMAGENET1K_V1`. You can also use `weights=ResNet18_Weights.DEFAULT` to get the most up-to-date weights.
warnings.warn(msg)
Downloading: "https://download.pytorch.org/models/resnet18-f37072fd.pth" to /root/.cache/torch/hub/checkpoints/resnet18-f37072fd.pth| epoch | train_loss | valid_loss | error_rate | time |
|---|---|---|---|---|
| 0 | 0.199976 | 0.072374 | 0.020298 | 00:19 |
| epoch | train_loss | valid_loss | error_rate | time |
|---|---|---|---|---|
| 0 | 0.061802 | 0.081512 | 0.020974 | 00:20 |
| 1 | 0.047748 | 0.030506 | 0.010149 | 00:18 |
| 2 | 0.021600 | 0.026245 | 0.006766 | 00:18 |
# export our trained learner
learn.export('model.pkl')- Following the script in the video, as well as the
git-lfsandrequirements.txtin Tanishq Abraham’s tutorial, I deployed a Dog and Cat Classifier on HuggingFace Spaces. - If you run the training for long enough (high number of epochs) the error rate will get worse. We’ll learn why in a future lesson.
- Use fastsetup to setup your local machine with Python and Jupyter.
- They recommend using mamba instead of conda as it is faster.
Notebook Exercise
In the cells below, I’ll run the code provided in the Chapter 2 notebook.
# prepare path and subfolder names
bear_types = 'grizzly', 'black', 'teddy'
path = Path('bears')# download images of grizzly, black and teddy bears
if not path.exists():
path.mkdir()
for o in bear_types:
dest = (path/o)
dest.mkdir(exist_ok = True)
results = search_images_ddg(f'{o} bear')
download_images(dest, urls = results)# view file paths
fns = get_image_files(path)
fns(#570) [Path('bears/grizzly/ca9c20c9-e7f4-4383-b063-d00f5b3995b2.jpg'),Path('bears/grizzly/226bc60a-8e2e-4a18-8680-6b79989a8100.jpg'),Path('bears/grizzly/2e68f914-0924-42ed-9e2e-19963fa03a37.jpg'),Path('bears/grizzly/38e2d057-3eb2-4e8e-8e8c-fa409052aaad.jpg'),Path('bears/grizzly/6abc4bc4-2e88-4e28-8ce4-d2cbdb05d7b5.jpg'),Path('bears/grizzly/3c44bb93-2ac5-40a3-a023-ce85d2286846.jpg'),Path('bears/grizzly/2c7b3f99-4c8e-4feb-9342-dacdccf60509.jpg'),Path('bears/grizzly/a59f16a6-fa06-42d5-9d79-b84e130aa4e3.jpg'),Path('bears/grizzly/d1be6dc8-da42-4bee-ac31-0976b175f1e3.jpg'),Path('bears/grizzly/7bc0d3bd-a8dd-477a-aa16-449124a1afb5.jpg')...]# get list of corrupted images
failed = verify_images(fns)
failed(#24) [Path('bears/grizzly/2e68f914-0924-42ed-9e2e-19963fa03a37.jpg'),Path('bears/grizzly/f77cfeb5-bfd2-4c39-ba36-621f117a65f6.jpg'),Path('bears/grizzly/37aa7eed-5a83-489d-b8f5-54020ba41390.jpg'),Path('bears/black/90a464ad-b0a7-4cf5-86ff-72d507857007.jpg'),Path('bears/black/f03a0ceb-4983-4b8f-a001-84a0875704e8.jpg'),Path('bears/black/6193c1cf-fda4-43f9-844e-7ba7efd33044.jpg'),Path('bears/teddy/474bdbb3-de2f-49e5-8c5b-62b4f3f50548.JPG'),Path('bears/teddy/58755f3f-227f-4fad-badc-a7d644e54296.JPG'),Path('bears/teddy/eb55dc00-3d01-4385-a7da-d81ac5211696.jpg'),Path('bears/teddy/97eadc96-dc4e-4b3f-8486-88352a3b2270.jpg')...]# remove corrupted image files
failed.map(Path.unlink)(#24) [None,None,None,None,None,None,None,None,None,None...]# create DataBlockfor training
bears = DataBlock(
blocks = (ImageBlock, CategoryBlock),
get_items = get_image_files,
splitter = RandomSplitter(valid_pct = 0.2, seed = 42),
get_y = parent_label,
item_tfms = Resize(128)
)# create DataLoaders object
dls = bears.dataloaders(path)# observe how images react to the "squish" ResizeMethod
bears = bears.new(item_tfms = Resize(128, ResizeMethod.Squish))
dls = bears.dataloaders(path)
dls.valid.show_batch(max_n = 4, nrows = 1)Notice how the grizzlies in the third image look abnormally skinny, since the image is squished.
# observe how images react to the "pad" ResizeMethod
bears = bears.new(item_tfms = Resize(128, ResizeMethod.Pad, pad_mode = 'zeros'))
dls = bears.dataloaders(path)
dls.valid.show_batch(max_n = 4, nrows = 1)In these images, the original aspect ratio is maintained.
# observe how images react to the transform RandomResizedCrop
bears = bears.new(item_tfms = RandomResizedCrop(128, min_scale = 0.3))
dls = bears.dataloaders(path)
dls.valid.show_batch(max_n = 4, nrows = 1)# observe how images react to data augmentation transforms
bears = bears.new(item_tfms=Resize(128), batch_tfms = aug_transforms(mult = 2))
dls = bears.dataloaders(path)
# note that data augmentation occurs on training set
dls.train.show_batch(max_n = 8, nrows = 2, unique = True)# train the model in order to clean the data
bears = bears.new(
item_tfms = RandomResizedCrop(224, min_scale = 0.5),
batch_tfms = aug_transforms())
dls = bears.dataloaders(path)
dls.show_batch()# train the model
learn = vision_learner(dls, resnet18, metrics = error_rate)
learn.fine_tune(4)/usr/local/lib/python3.10/dist-packages/torchvision/models/_utils.py:208: UserWarning: The parameter 'pretrained' is deprecated since 0.13 and may be removed in the future, please use 'weights' instead.
warnings.warn(
/usr/local/lib/python3.10/dist-packages/torchvision/models/_utils.py:223: UserWarning: Arguments other than a weight enum or `None` for 'weights' are deprecated since 0.13 and may be removed in the future. The current behavior is equivalent to passing `weights=ResNet18_Weights.IMAGENET1K_V1`. You can also use `weights=ResNet18_Weights.DEFAULT` to get the most up-to-date weights.
warnings.warn(msg)
Downloading: "https://download.pytorch.org/models/resnet18-f37072fd.pth" to /root/.cache/torch/hub/checkpoints/resnet18-f37072fd.pth
100%|██████████| 44.7M/44.7M [00:00<00:00, 100MB/s] | epoch | train_loss | valid_loss | error_rate | time |
|---|---|---|---|---|
| 0 | 1.221027 | 0.206999 | 0.055046 | 00:34 |
| epoch | train_loss | valid_loss | error_rate | time |
|---|---|---|---|---|
| 0 | 0.225023 | 0.177274 | 0.036697 | 00:32 |
| 1 | 0.162711 | 0.189059 | 0.036697 | 00:31 |
| 2 | 0.144491 | 0.191644 | 0.027523 | 00:31 |
| 3 | 0.122036 | 0.188296 | 0.018349 | 00:31 |
# view Confusion Matrix
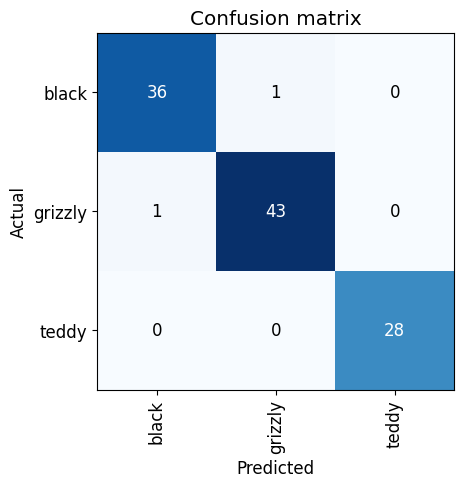
interp = ClassificationInterpretation.from_learner(learn)
interp.plot_confusion_matrix()The model confused a grizzly for a black bear and a black bear for a grizzly bear. It didn’t confuse any of the teddy bears, which makes sense given how different they look to real bears.
The fourth image has two humans in it, which is likely why the model didn’t recognize the bear. The model correctly predicted the the third and fifth images but with low confidence (57% and 69%).
# clean the training and validation sets
from fastai.vision.widgets import *
cleaner = ImageClassifierCleaner(learn)
cleanerI cleaned up the images (deleting an image of a cat, another of a cartoon bear, a dog, and a blank image).
# delete or move images based on the dropdown selections made in the cleaner
for idx in cleaner.delete(): cleaner.fns[idx].unlink()
for idx,cat in cleaner.change(): shutil.move(str(cleaner.fns[idx]), path/cat)# create new dataloaders object
bears = bears.new(
item_tfms = RandomResizedCrop(224, min_scale = 0.5),
batch_tfms = aug_transforms())
dls = bears.dataloaders(path)
dls.show_batch()# retrain the model
learn = vision_learner(dls, resnet18, metrics = error_rate)
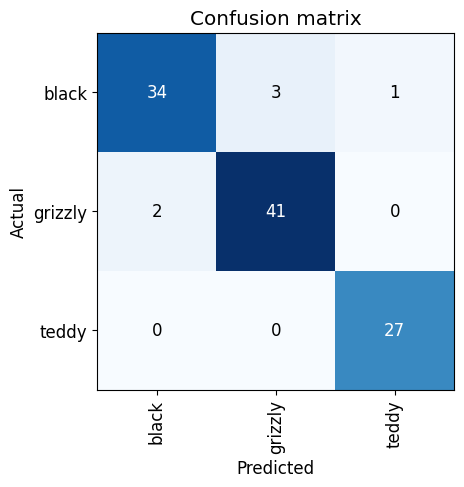
learn.fine_tune(4)| epoch | train_loss | valid_loss | error_rate | time |
|---|---|---|---|---|
| 0 | 1.289331 | 0.243501 | 0.074074 | 00:32 |
| epoch | train_loss | valid_loss | error_rate | time |
|---|---|---|---|---|
| 0 | 0.225567 | 0.256021 | 0.064815 | 00:32 |
| 1 | 0.218850 | 0.288018 | 0.055556 | 00:34 |
| 2 | 0.184954 | 0.315183 | 0.055556 | 00:31 |
| 3 | 0.141363 | 0.308634 | 0.055556 | 00:31 |
Weird!! After cleaning the data, the model got worse (1.8% error rate is now 5.6%). I’ll run the cleaning routine again and retrain the model to see if it makes a difference. Perhaps there are still erroneous images in the mix.
# view Confusion Matrix
interp = ClassificationInterpretation.from_learner(learn)
interp.plot_confusion_matrix()This time, the model incorrectly predicted 3 grizzlies as black bears, 2 black bears as grizzlies and 1 black bear as a teddy.
cleaner = ImageClassifierCleaner(learn)
cleaner# delete or move images based on the dropdown selections made in the cleaner
for idx in cleaner.delete(): cleaner.fns[idx].unlink()
for idx,cat in cleaner.change(): shutil.move(str(cleaner.fns[idx]), path/cat)# create new dataloaders object
bears = bears.new(
item_tfms = RandomResizedCrop(224, min_scale = 0.5),
batch_tfms = aug_transforms())
dls = bears.dataloaders(path)
# The lower right image (cartoon bear) is one that I selected "Delete" for
# in the cleaner so I'm not sure why it's still there
# I'm wondering if there's something wrong with the cleaner or how I'm using it?
dls.show_batch()# retrain the model
learn = vision_learner(dls, resnet18, metrics = error_rate)
learn.fine_tune(4)| epoch | train_loss | valid_loss | error_rate | time |
|---|---|---|---|---|
| 0 | 1.270627 | 0.130137 | 0.046729 | 00:31 |
| epoch | train_loss | valid_loss | error_rate | time |
|---|---|---|---|---|
| 0 | 0.183445 | 0.078030 | 0.028037 | 00:32 |
| 1 | 0.201080 | 0.053461 | 0.018692 | 00:33 |
| 2 | 0.183515 | 0.019479 | 0.009346 | 00:37 |
| 3 | 0.144900 | 0.012682 | 0.000000 | 00:31 |
I’m still not confident that this is a 100% accurate model given the bad images in the training set (such as the cartoon bear) but I’m going to go with it for now.
Book Notes
Chapter 2: From Model to Production
- Underestimating the constraints and overestimating the capabilities of deep learning may lead to frustratingly poor results, at least until you gain some experience and can solve the problems that arise.
- Overstimating the constraints and underestimating the capabilities of deep learning may mean you do not attempt a solvable problem because you talk yourself out of it.
- The most important thing (as you learn deep learning) is to ensure that you have a project to work on.
- The goal is not to find the “perfect” dataset or project, but just to get started and iterate from there.
- Complete every step as well as you can in a reasonable amount of time, all the way to the end.
- Computer vision
- Object recognition: recognize items in an image
- Object detection: recognition + highlight the location and name of each found object.
- Deep learning algorithms are generally not good at recognizing images that are significantly different in structure or style from those used to train the model.
- NLP
- Deep learning is not good at generating correct responses.
- Text generation models will always be technologically a bit ahead of models for recognizing automatically generated text.
- Google’s online translation system is based on deep learning.
- Combining text and images
- A deep learning model can be trained on input images with output captions written in English, and can learn to generate surprisingly appropriate captions automatically for new images (with no guarantee the captions will be correct).
- Deep learning should be used not as an entirely automated process, but as part of a process in which the model and a human user interact closely.
- Tabular data
- If you already have a system that is using random forests or gradient boosting machines then switching to or adding deep learning may not result in any dramatic improvement.
- Deep learning greatly increases the variety of columns that you can include.
- Deep learning models generally take longer to train than random forests or gradient boosting machines.
- Recommendation systems
- A special type of tabular data (a high-cardinality categorical variable representing users and another one representing products or something similar).
- Deep learning models are good at handling high cardinality categorical variables and thus recommendation systems.
- Deep learning models do well when combining these variables with other kinds of data such as natural language, images, or additional metadata represented as tables such as user information, previous transactions, and so forth.
- Nearly all machine learning approaches have th downside that they tell you only which products a particular user might like, rather than what recommendations would be helpful for a user.
- Other data types
- Using NLP deep learning methods is the current SOTA approach for many types of protein analysis since protein chains look a lot like natural language documents.
- The Drivetrain Approach
- Defined objective
- Levers (what inputs can we control)
- Data (what inputs we can collect)
- Models (how the levers influence the objective)
- Gathering data
- For most projects you can find the data online.
- Use
duckduckgo_search
- From Data to DataLoaders
DataLoadersis a thin class that just stores whateverDataLoaderobjects you pass to it and makes them available astrainandvalid.- To turn data into a
DataLoadersobject we need to tell fastai four things:- What kinds of data we are working with.
- How to get the list of items.
- How to label these items.
- How to create the validation set.
- With the
DataBlockAPI you can customize every stage of the creation of yourDataLoaders:
bears = DataBlock(
blocks=(ImageBlock, CategoryBlock),
get_items=get_image_files,
splitter=RandomSplitter(valid_pct=0.2, seed=42),
get_y=parent_label,
item_tfms=Resize(128))- explanation of
DataBlockblocksspecifies types for independent (the thing we are using to make predictions from) and dependent (our target) variables.- Computers don’t really know how to create random numbers at all, but simply create lists of numbers that look random; if you provide the same starting point for that list each time–called the seed–then you will get the exact same list each time.
- Images need to be all the same size.
- A
DataLoaderis a class that provides batches of a few items at a time to the GPU. - fastai default batch size is 64 items.
Resizecrops the images to fit a square shape, alternatively you can pad (ResizeMethod.Pad) or squish (ResizeMethod.Squish) the images to fit the square.- Squishing (model learns that things look differently from how they actually are), cropping (removal of features that would allow us to perform recognition) and padding (lot of empty space which is just wasted computation) are wasteful or problematic approaches. Instead, randomly select part of the image and then crop to just that part. On each epoch, we randomly select a different part of each image (
RandomResizedCrop(min_scale)). - Training the neural network with examples of images in which objects are in slightly different places and are slightly different sizes helps it to understand the basic concept of what an object is and how it can be represented in an image.
- Data Augmentation
- refers to creating random variations of our input data, such that they appear different but do not change the meaning of the data (rotation, flipping, perspective warping, brightness changes, and contrast changes).
aug_transforms()provides a standard set of augmentations.- Use
batch_tfmsto process a batch at a time on the GPU to save time.
- Training your model and using it to clean your data
- View confusion matrix with
ClassificationInterpretation.from_learner(learn). The diagonal shows images that are classified correctly. Calculated using validation set. - Sort images by loss using
interp.plot_top_losses(). - Loss is high if the model is incorrect (especially if it’s also confident) or if it’s correct but not confident.
- A model can help you find data issues more quickly.
- View confusion matrix with
- Using the model for inference
learn.export()will export a .pkl file.- Get predictions with
learn_inf.predict(<input>). This returns three things: the predicted category in the same format you originally provided, the index of the predicted category and the probabilities for each category. - You can access the
DataLoadersas an attribute of theLearner:learn_inf.dls.
- Deploying your app
- You almost certainly do not need a GPU to serve your model in production.
- To classify a few users’ images at a time, you need high-volume. If you do have this scenario, use Microsoft’s ONNX Runtime or AWS SageMaker.
- Recommended wherever possible to deploy the model itself to a server and have your mobile/edge application connect to it as a web service.
- If your application uses sensitive data, your users may be concerned about an approach that sends that data to a remote server.
- How to Avoid Disaster
- Understanding and testing the behavior of a deep learning model is much more difficult than with most other code you write.
- The kinds of photos that people are most likely to upload to the internet are the kinds of photos that do a good job of clearly and artistically displaying their subject matter, which isn’t the kind of input this system is going to be getting in real life. We may need to do a lot of our own data collection and labeling to create a useful system.
- out-of-domain data: data that our model sees in production that is very different from what it saw during training.
- domain shift: data that our model sees changes over time.
- Deployment process
- Manual Process: run model in parallel, humans check all predictions.
- Limited scope deployment: careful human supervision, time or geography limited.
- Gradual expansion: good reporting systems needed, consider what could go wrong.
- Unforeseen consequences and feedback loops
- Your model may change the behavior of the system it’s a part of.
- feedback loops can result in negative implications of bias getting worse.
- A helpful exercise prior to rolling out a significant machine learning system is to consider the question “What would happen if it went really, really well?”
- Questionnaire
- Where do text models currently have a major deficiency?
- Providing correct or accurate information.
- What are possible negative societal implications of text generation models?
- The viral spread of misinformation, which can lead to real actions and harms.
- In situations where a model might make mistakes, and those mistakes could be harmful, what is a god alternative to automating a process?
- Run the model in parallel with a human checking its predictions.
- What kind of tabular data is deep learning particularly good at?
- High-cardinality categorical data.
- What’s a key downside of directly using a deep learning model for recommendation systems?
- It will only tell you which products a particular user might like, rather than what recommendations may be helpful for a user.
- What are the steps of the Drivetrain Approach?
- Define an objective
- Determine what inputs (levers) you can control
- Collect data
- Create models (how the levers influence the objective)
- How do the steps of the Drivetrain Approach map to a recommendation system?
- Objective: drive additional sales due to recommendations.
- Level: ranking of the recommendations.
- Data: must be collectd to generate recommendations that will cause new sales.
- Models: two for purchasing probabilities conditional on seeing or not seeing a recommendation, the difference between these two probabilities is a utility function for a given recommendation to a customer (low in cases when algorithm recommends a familiar book that the customer has already rejected, or a book they would have bought even without the recommendation).
- Create an image recognition model using data you curate, and deploy it on the web.
- Here.
- What is
DataLoaders?- A class that creates validation and training sets/batches that are fed to the GPUS
- What four things do we need to tell fastai to create
DataLoaders?- What kinds of data we are working with (independent and dependent variables).
- How to get the list of items.
- How to label these items.
- How to create the validation set.
- What does the
splitterparameter toDataBlockdo?- Set aside a percentage of the data as the validation set.
- How do we ensure a random split always gives the same validation set?
- Set the
seedparameter to the same value.
- Set the
- What letters are often used to signify the independent and dependent variables?
- Independent: x
- Dependent: y
- What’s the difference between crop, pad and squish resize approaches? When might you choose one over the others?
- Crop: takes a section of the image and resizes it to the desired size. Use when it’s not necessary to have the model traing on the whole image.
- Pad: keep the image aspect ratio as is, add white/black padding to make a square. Use when it’s necessary to have the model train on the whole image.
- Squish: distorts the image to fit a square. Use when it’s not necessary to have the model train on the original aspect ratio.
- What is data augmentation? Why is it needed?
- Data augmentation is the creation of random variations of input data through techniques like rotation, flipping, brightness changes, contrast changes, perspective warping. It is needed to help the model learn to recognize objects under different lighting/perspective conditions.
- Provide an example of where the bear classification model might work poorly in production, due to structural or style differences in the training data.
- What is the difference between
item_tfmsandbatch_tfms?item_tfmsare transforms that are applied to each item in the set.batch_tfmsare transforms applied to a batch of items in the set.
- What is a confusion matrix?
- A matrix that shows the counts of predicted (columns) vs. actual (rows) labels, with the diagonal being correctly predicted data.
- What does
exportsave?- Both the architecture and the parameters as a
.pklfile.
- Both the architecture and the parameters as a
- What is called when we use a model for making predictions, instead of training?
- Inference
- What are IPython widgets?
- interactive browser controls for Jupyter Notebooks.
- When would you use a CPU for deployment? When might a GPU be better?
- CPU: low-volume, single-user inputs for prediction.
- GPU: high-volume, multiple-user inputs for predictions.
- What are the downsides of deploying your app to a server, instead of to a client (or edge) device such as a phone or PC?
- Requires internet connectivity (and latency).
- Sensitive data transfer may not be okay with your users.
- Managing complexity and scaling the server creates additional overhead.
- What are three examples of problems that could occur when rolling out a bear warning system in practice?
- out-of-domain data: the images captured of real bears may not be represented in the model’s training or validation datasets.
- Number of bear alerts doubles or halves after rollout of the new system in some location.
- out-of-domain data: the cameras may capture low-resolution images of the bears when the training and validation set had high resolution images.
- What is out-of-domain data?
- Data your model sees in production that it hasn’t seen during training.
- What is domain shift?
- Changes in the data that our model sees in production over time.
- What are the three steps in the deployment process?
- Manual Process
- Limited scope deployment
- Gradual expansion
- Where do text models currently have a major deficiency?
- Further Research
- Consider how the Drivetrain Approach maps to a project or problem you’re interested in.
- I’ll take the example of a project I will be working on to practice what I’m learning in this book: training a deep learning model which correctly classifies the typeface from a collection of single letter.
- The objective: correctly classify typeface from a collection of single letters.
- Levers: observe key features of key letters that are the “tell” of a typeface.
- Data: using an HTML canvas object and Adobe Fonts, generate images of single letters of multiple fonts associated with each category of typeface.
- Models: output the probabilities of each typeface a given collection of single letters is predicted as. This allows for some flexibility in how you categorize letters based on the shared characteristics of more than one typeface that the particular font may possess.
- I’ll take the example of a project I will be working on to practice what I’m learning in this book: training a deep learning model which correctly classifies the typeface from a collection of single letter.
- When might it be best to avoid certain types of data augmentation?
- In my typeface example, it’s best to avoid perspective warping because it will change key features used to recognize a typeface.
- For a project you’re interested in applying deep learning to, consider the thought experiment, “What would happen if it went really, really well?”
- If my typeface classifier works really well, I imagine it would be used by people to take pictures of real-world text and learn what typeface it is. This may inspire a new wave of typeface designers. If a feedback loop was possible, and the classifier went viral, the very definition of typefaces may be affected by popular opinion. Taken a step further, a generative model may be inspired by this classifier, and a new wave of AI typeface would be launched—however this last piece is highly undesirable unless the training of the model involves appropriate licensing and attribution of the typefaces used that are created by humans. Furthermore, from what I understand from reading about typefaces, the process of creating a typeface is an amazing experience and should not be replaced with AI generators. If I created such a generative model (in part 2 of the course) and it went viral (do HuggingFace Spaces go viral? Cuz that’s where I would launch it), I would take it down.
- Start a blog (done!)
- Consider how the Drivetrain Approach maps to a project or problem you’re interested in.
Lesson 3: Neural Net Foundations
Video Notes
Link to this lesson’s video.
- How to do a fast.ai lesson
- Watch lecture
- Run notebook & experiment
- Reproduce results
- Repeat with different dataset
- fastbook repo contains “clean” folder with notebooks without markdown text.
- Two concepts: training the model and using it for inference.
- Over 500 architectures in
timm(PyTorch Image Models). timm.list_models(pattern)will list models matching the pattern.- Pass string name of timm model to the
Learnerlike:vision_learner(dls, 'timm model string', ...). in22= ImageNet with 22k categories,1k= ImageNet with 1k categories.learn.predictprobabilities are in the order oflearn.dls.vocab.learn.modelcontains the trained model which contains lots of nested layers.learn.model.get_submoduletakes a dotted string navigating through the hierarchy.- Machine learning models fit functions to data.
- Things between dollar signs is LaTeX
"$...$". - General form of quadratic:
def quad(a,b,c,x): return a*x**2 + b*x + c partialfromfunctoolsfixes parameters to a function.- Loss functions tells us how good our model is.
@interactfromipywidgetsallows sliders tied to the function its above.- Mean Squared Error:
def mse(preds, acts): return ((preds - acts)**2).mean() - For each parameter we need to know: does the loss get better when we increase or decrease the parameter?
- The derivative is the function that tells you: if you increase the input does the output increase or decrease, and by how much?
*paramsspreads out the list into its elements and passes each to the function.- 1-D (rank 1) tensor (lists of numbers), 2-D tensor (tables of numbers) 3-D tensor (layers of tables of numbers) and so on.
tensor.requires_grad_()calculates the gradient of the values in the tensor whenever its used in calculation.loss.backward()calculates gradients on the inputs to the loss function.abc.gradattribute added after gradients are calculated.- negative gradient means increasing the parameter will decrease the loss.
- update parameters
with torch.no_grad()so PyTorch doesn’t calculate the gradient (since it’s being used in a function). We don’t want the derivative of the parameter update, we only want the derivative with respect to the loss. - Automate the steps
- Calculate Mean Squared Error
- Call
.backward. - Subtract gradient * small number from the parameters
- All optimizers are built on the concept of gradient descent (calculate gradients and decrease the loss).
- We need a better function than quadratics
- Rectified Linear Unit:
def rectified_linear(m,b,x):
y = m*x + b
return torch.clip(y, 0.)torch.clipturns values less than value specified to the value specified (in this case, it turns negative values to 0.).- Adding rectified linear functions together gives us an arbitrarily squiggly function that will match as close as we want to the data.
- ReLU in 2D gives you surfaces, volumes in 3D, etc.
- With this incredibly simple foundation you can construct an arbitrarily precise, accurate model.
- When you have ReLU’s getting added together, and gradient descent to optimize the parameters, and samples of inputs and outputs that you want, the computer “draws the owl” so to speak.
- Deep learning is using gradient descent to set some parameters to make a wiggly function (the addition of lots of rectified linear units or something very similar to that) that matches your data.
- When selecting an architecture, the biggest beginner mistake is that they jump to the highest-accuracy models.
- At the start of the project, just use resnet18 so you can spend all of your time trying things out (data augmentation, data cleaning, different external data) as fast as possible.
- Trying better architectures is the very last thing to do.
- How do I know if I have enough data?
- Vast majority of projects in industry wait far too long until they train their first model.
- Train your first model on day 1 with whatever CSV files you can hack together.
- Semi-supervised training lets you get dramatically more out of your data.
- Often it’s easy to get lots of inputs but hard to get lots of outputs (labels).
- Units of parameter gradients: for each increase in parameter of 1, the gradient is the amount the loss would change by (if it stayed at that slope—which it doesn’t because it’s a curve).
- Once you get close enough to the optimal parameter value, all loss functions look like quadratics
- The slope of the loss function decreases as you approach the optimal
- Learning rate (a hyperparameter) is multiplied by the gradient, the product of which is subtracted from the parameters
- If you pick a learning rate that’s too large, you will diverge; if you pick too small, it’ll take too long to train.
- http://matrixmultiplication.xyz/
- Matrix multiplication is the critical foundational mathematical operation in deep learning
- GPUs are good at matrix multiplication with tensor cores (multiply together two 4x4 matrices)
- Use a spreadsheet to train a deep learning model on the Kaggle Titanic dataset in which you’re trying to predict if a person survived.
- Columns included (convert some of them to binary categorical variables):
- Survivor
- Pclass
- Convert to Pclass_1 and Pclass_2 (both 1/0).
- Sex
- Convert to Male (0/1) column.
- Age
- Remove blanks.
- Normalize (Age/Max(Age))
- SibSp (how many siblings they have)
- Parch (# of parents/children aboard)
- Fare
- Lots of very small and very large fares, log of it has a much more even distribution. (LOG10(Fare + 1).
- Embarked (which city they got on at)
- Remove blanks.
- Convert to Embark_S and Embark_C (both 1/0)
- Ones
- Add a column of 1s.
- Create random numbers for params (including Const) with
=RAND() - 0.5. - Regression
- Use
SUMPRODUCTto calculate linear function. - Loss of linear function is (linear function result - Survived) ^ 2.
- Average loss = AVERAGE(individual losses).
- User “Solver” with GRG Nonlinear Solving Method. Set Objective to minimize the cell with average loss. Change parameter variables.
- Use
- Neural Net
- Two sets of params.
- Two linear columns.
- Two ReLU columns.
- Adding two linear functions together gives you a linear function, we want all those wiggles (non-linearity) so we use ReLUs.
- ReLU:
IF(lin1 < 0, 0, lin1) - Preds = sum of the two ReLUs.
- Loss same as regression.
- Solver process the same as well.
- Neural Net (Matrix Multiplication)
- Transpose params into two columns.
=MMULT(...)for Lin1 and Lin2 columns.- Keep ReLU, Preds and Loss column the same.
- Optimize params using Solver.
- Helpful reminder to build intuition around matrix multiplication: it’s doing the same thing as the
SUMPRODUCTs.
- Dummy variables: Pclass_1, Pclass_2, etc.
- Columns included (convert some of them to binary categorical variables):
- Next lesson: NLP
- It’s about making predictions with text data which most of the time is in the form of prose.
- First Farsi NLP resource was created by a student of the first fastai course.
- NLP most commonly and practically used for classification.
- Document = one or two words, a book, a wikipedia page, any length.
- Classification = figure out a category for a document.
- Sentiment analysis
- Author identification
- Legal discovery (is this document in-scope or out-of-scope)
- Organizing documents by topic
- Triaging inbound emails
- Classification of text looks similar to images.
- We’re going to use a different library: HuggingFace Transformers
- Helpful to see how things are done in more than one library.
- HuggingFace Transformers doesn’t have the same high-level API. Have to do more stuff manually. Which is good for students at this point of the course.
- It’s a good library.
- Before the next lesson take a look at the NLP notebook and U.S. Patent to Phrase Matching data.
- Trying to figure out in patents whether two concepts are referring to the same thing. The document is text1, text2, and the category is similar (1) or not-similar (0).
- Will also talk about the two very important topics of validation sets and metrics.
Notebook Exercise
Training and Deploying: Pets Classifier
In this section, I’ll train a Pets dataset classifier as done by Jeremy in this notebook.
from fastai.vision.all import *
import timmpath = untar_data(URLs.PETS)/'images'
# Create DataLoaders object
dls = ImageDataLoaders.from_name_func('.',
get_image_files(path),
valid_pct=0.2,
seed=42,
label_func=RegexLabeller(pat = r'^([^/]+)_\d+'),
item_tfms=Resize(224))# train using resnet34 as architecture
learn = vision_learner(dls, resnet34, metrics=error_rate)
learn.fine_tune(3)/usr/local/lib/python3.10/dist-packages/torchvision/models/_utils.py:208: UserWarning: The parameter 'pretrained' is deprecated since 0.13 and may be removed in the future, please use 'weights' instead.
warnings.warn(
/usr/local/lib/python3.10/dist-packages/torchvision/models/_utils.py:223: UserWarning: Arguments other than a weight enum or `None` for 'weights' are deprecated since 0.13 and may be removed in the future. The current behavior is equivalent to passing `weights=ResNet34_Weights.IMAGENET1K_V1`. You can also use `weights=ResNet34_Weights.DEFAULT` to get the most up-to-date weights.
warnings.warn(msg)
Downloading: "https://download.pytorch.org/models/resnet34-b627a593.pth" to /root/.cache/torch/hub/checkpoints/resnet34-b627a593.pth
100%|██████████| 83.3M/83.3M [00:00<00:00, 196MB/s]| epoch | train_loss | valid_loss | error_rate | time |
|---|---|---|---|---|
| 0 | 1.496086 | 0.316146 | 0.100135 | 01:12 |
| epoch | train_loss | valid_loss | error_rate | time |
|---|
| epoch | train_loss | valid_loss | error_rate | time |
|---|---|---|---|---|
| 0 | 0.441153 | 0.315289 | 0.093369 | 01:04 |
| 1 | 0.289844 | 0.215224 | 0.069012 | 01:05 |
| 2 | 0.123374 | 0.191152 | 0.060217 | 01:03 |
The pets classifier, using resnet34 and 3 epochs, is about 94% accurate.
# train using a timm architecture
# from the convnext family of architectures
learn = vision_learner(dls, 'convnext_tiny_in22k', metrics=error_rate).to_fp16()
learn.fine_tune(3)/usr/local/lib/python3.10/dist-packages/timm/models/_factory.py:114: UserWarning: Mapping deprecated model name convnext_tiny_in22k to current convnext_tiny.fb_in22k.
model = create_fn(| epoch | train_loss | valid_loss | error_rate | time |
|---|---|---|---|---|
| 0 | 1.130913 | 0.240275 | 0.085927 | 01:06 |
| epoch | train_loss | valid_loss | error_rate | time |
|---|---|---|---|---|
| 0 | 0.277886 | 0.193888 | 0.061570 | 01:08 |
| 1 | 0.196232 | 0.174544 | 0.055480 | 01:09 |
| 2 | 0.127525 | 0.156720 | 0.048038 | 01:07 |
Using convnext_tiny_in22k, the model is about 95.2% accurate, about a 20% decrease in error rate.
# export to use in gradio app
learn.export('pets_model.pkl')You can view my pets classifier gradio app here.
Which image models are best?
In this section, I’ll plot the timm model results as shown in Jeremy’s notebook.
import pandas as pd# load data
df_results = pd.read_csv("../../../fastai-course/data/results-imagenet.csv")
df_results.head()| model | top1 | top1_err | top5 | top5_err | param_count | img_size | crop_pct | interpolation | |
|---|---|---|---|---|---|---|---|---|---|
| 0 | eva02_large_patch14_448.mim_m38m_ft_in22k_in1k | 90.052 | 9.948 | 99.048 | 0.952 | 305.08 | 448 | 1.0 | bicubic |
| 1 | eva02_large_patch14_448.mim_in22k_ft_in22k_in1k | 89.966 | 10.034 | 99.012 | 0.988 | 305.08 | 448 | 1.0 | bicubic |
| 2 | eva_giant_patch14_560.m30m_ft_in22k_in1k | 89.786 | 10.214 | 98.992 | 1.008 | 1,014.45 | 560 | 1.0 | bicubic |
| 3 | eva02_large_patch14_448.mim_in22k_ft_in1k | 89.624 | 10.376 | 98.950 | 1.050 | 305.08 | 448 | 1.0 | bicubic |
| 4 | eva02_large_patch14_448.mim_m38m_ft_in1k | 89.570 | 10.430 | 98.922 | 1.078 | 305.08 | 448 | 1.0 | bicubic |
top1 = what percent of the time the model predicts the correct label with the highest probability.
top5 = what percent of the time the model predits the correct label with the top 5 highest probabilities.
# remove additional text from model name
df_results['model_org'] = df_results['model']
df_results['model'] = df_results['model'].str.split('.').str[0]
df_results.head()| model | top1 | top1_err | top5 | top5_err | param_count | img_size | crop_pct | interpolation | model_org | |
|---|---|---|---|---|---|---|---|---|---|---|
| 0 | eva02_large_patch14_448 | 90.052 | 9.948 | 99.048 | 0.952 | 305.08 | 448 | 1.0 | bicubic | eva02_large_patch14_448.mim_m38m_ft_in22k_in1k |
| 1 | eva02_large_patch14_448 | 89.966 | 10.034 | 99.012 | 0.988 | 305.08 | 448 | 1.0 | bicubic | eva02_large_patch14_448.mim_in22k_ft_in22k_in1k |
| 2 | eva_giant_patch14_560 | 89.786 | 10.214 | 98.992 | 1.008 | 1,014.45 | 560 | 1.0 | bicubic | eva_giant_patch14_560.m30m_ft_in22k_in1k |
| 3 | eva02_large_patch14_448 | 89.624 | 10.376 | 98.950 | 1.050 | 305.08 | 448 | 1.0 | bicubic | eva02_large_patch14_448.mim_in22k_ft_in1k |
| 4 | eva02_large_patch14_448 | 89.570 | 10.430 | 98.922 | 1.078 | 305.08 | 448 | 1.0 | bicubic | eva02_large_patch14_448.mim_m38m_ft_in1k |
def get_data(part, col):
# get benchmark data and merge with model data
df = pd.read_csv(f'../../../fastai-course/data/benchmark-{part}-amp-nhwc-pt111-cu113-rtx3090.csv').merge(df_results, on='model')
# convert samples/sec to sec/sample
df['secs'] = 1. / df[col]
# pull out the family name from the model name
df['family'] = df.model.str.extract('^([a-z]+?(?:v2)?)(?:\d|_|$)')
# removing `resnetv2_50d_gn` and `resnet50_gn` for some reason
df = df[~df.model.str.endswith('gn')]
# not sure why the following line is here, "in22" was removed in cell above
df.loc[df.model.str.contains('in22'),'family'] = df.loc[df.model.str.contains('in22'),'family'] + '_in22'
df.loc[df.model.str.contains('resnet.*d'),'family'] = df.loc[df.model.str.contains('resnet.*d'),'family'] + 'd'
# only returns subset of families
return df[df.family.str.contains('^re[sg]netd?|beit|convnext|levit|efficient|vit|vgg|swin')]# load benchmark inference data
df = get_data('infer', 'infer_samples_per_sec')
df.head()| model | infer_samples_per_sec | infer_step_time | infer_batch_size | infer_img_size | param_count_x | top1 | top1_err | top5 | top5_err | param_count_y | img_size | crop_pct | interpolation | model_org | secs | family | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 12 | levit_128s | 21485.80 | 47.648 | 1024 | 224 | 7.78 | 76.526 | 23.474 | 92.872 | 7.128 | 7.78 | 224 | 0.900 | bicubic | levit_128s.fb_dist_in1k | 0.000047 | levit |
| 13 | regnetx_002 | 17821.98 | 57.446 | 1024 | 224 | 2.68 | 68.746 | 31.254 | 88.536 | 11.464 | 2.68 | 224 | 0.875 | bicubic | regnetx_002.pycls_in1k | 0.000056 | regnetx |
| 15 | regnety_002 | 16673.08 | 61.405 | 1024 | 224 | 3.16 | 70.278 | 29.722 | 89.528 | 10.472 | 3.16 | 224 | 0.875 | bicubic | regnety_002.pycls_in1k | 0.000060 | regnety |
| 17 | levit_128 | 14657.83 | 69.849 | 1024 | 224 | 9.21 | 78.490 | 21.510 | 94.012 | 5.988 | 9.21 | 224 | 0.900 | bicubic | levit_128.fb_dist_in1k | 0.000068 | levit |
| 18 | regnetx_004 | 14440.03 | 70.903 | 1024 | 224 | 5.16 | 72.398 | 27.602 | 90.828 | 9.172 | 5.16 | 224 | 0.875 | bicubic | regnetx_004.pycls_in1k | 0.000069 | regnetx |
# plot the data
import plotly.express as px
w,h = 1000, 800
def show_all(df, title, size):
return px.scatter(df,
width=w,
height=h,
size=df[size]**2,
title=title,
x='secs',
y='top1',
log_x=True,
color='family',
hover_name='model_org',
hover_data=[size]
)
show_all(df, 'Inference', 'infer_img_size')# plot a subset of the data
subs = 'levit|resnetd?|regnetx|vgg|convnext.*|efficientnetv2|beit|swin'
def show_subs(df, title, size, subs):
df_subs = df[df.family.str.fullmatch(subs)]
return px.scatter(df_subs,
width=w,
height=h,
size=df_subs[size]**2,
title=title,
trendline='ols',
trendline_options={'log_x':True},
x='secs',
y='top1',
log_x=True,
color='family',
hover_name='model_org',
hover_data=[size])
show_subs(df, 'Inference', 'infer_img_size', subs)# plot inference speed vs parameter count
px.scatter(df,
width=w,
height=h,
x='param_count_x',
y='secs',
log_x=True,
log_y=True,
color='infer_img_size',
hover_name='model_org',
hover_data=['infer_samples_per_sec', 'family']
)# repeat plots for training data
tdf = get_data('train', 'train_samples_per_sec')
show_all(tdf, 'Training', 'train_img_size')# subset of training data
show_subs(tdf, 'Training', 'train_img_size', subs)How does a neural net really work?
In this section, I’ll recreate the content in Jeremy’s notebook here, where he walks through a quadratic example of training a function to match the data.
A neural network layer:
- Multiplies each input by a number of values. These values are known as parameters.
- Adds them up for each group of values.
- Replaces the negative numbers with zeros.
# helper functions
from ipywidgets import interact
from fastai.basics import *# helper functions
plt.rc('figure', dpi=90)
def plot_function(f, title=None, min=-2.1, max=2.1, color='r', ylim=None):
x = torch.linspace(min,max, 100)[:,None]
if ylim: plt.ylim(ylim)
plt.plot(x, f(x), color)
if title is not None: plt.title(title)In the plot_function definition, I’ll look into why [:,None] is added after torch.linspace(min, max, 100)
torch.linspace(-1, 1, 10), torch.linspace(-1, 1, 10).shape(tensor([-1.0000, -0.7778, -0.5556, -0.3333, -0.1111, 0.1111, 0.3333, 0.5556,
0.7778, 1.0000]),
torch.Size([10]))torch.linspace(-1, 1, 10)[:,None], torch.linspace(-1, 1, 10)[:,None].shape(tensor([[-1.0000],
[-0.7778],
[-0.5556],
[-0.3333],
[-0.1111],
[ 0.1111],
[ 0.3333],
[ 0.5556],
[ 0.7778],
[ 1.0000]]),
torch.Size([10, 1]))[:, None] adds a dimension to the tensor.
Next he fits a quadratic function to data:
In order to simulate “finding” or “learning” the right model fit, he creates a general quadratic function:
def quad(a, b, c, x): return a*x**2 + b*x + cand uses partial to make new quadratic functions:
def mk_quad(a, b, c): return partial(quad, a, b, c)f2functools.partial(<function quad at 0x148c6d000>, 3, 2, 1)quad<function __main__.quad(a, b, c, x)>Next he simulates noisy measurements of the quadratic f:
# `scale` parameter is the standard deviation of the distribution
def noise(x, scale): return np.random.normal(scale=scale, size=x.shape)
# noise function matches quadratic x + x^2 (with noise) + constant noise
def add_noise(x, mult, add): return x * (1+noise(x, mult)) + noise(x,add)np.random.seed(42)
x = torch.linspace(-2, 2, steps=20)[:, None]
y = add_noise(f(x), 0.15, 1.5)# values match Jeremy's
x[:5], y[:5](tensor([[-2.0000],
[-1.7895],
[-1.5789],
[-1.3684],
[-1.1579]]),
tensor([[11.8690],
[ 6.5433],
[ 5.9396],
[ 2.6304],
[ 1.7947]], dtype=torch.float64))# overlay data with variable quadratic
@interact(a=1.1, b=1.1, c=1.1)
def plot_quad(a, b, c):
plt.scatter(x, y)
plot_function(mk_quad(a, b, c), ylim=(-3,13))Important note changing sliders: only after changing b and c values do you realize that a also needs to be changed.
Next, he creates a measure for how well the quadratic fits the data, mean absolute error (distance from each data point to the curve).
def mae(preds, acts): return (torch.abs(preds-acts)).mean()# update interactive plot
@interact(a=1.1, b=1.1, c=1.1)
def plot_quad(a, b, c):
f = mk_quad(a,b,c)
plt.scatter(x,y)
loss = mae(f(x), y)
plot_function(f, ylim=(-3,12), title=f"MAE: {loss:.2f}")In a neural network we’ll have tens of millions or more parameters to fit and thousands or millions of data points to fit them to, which we can’t do manually with sliders. We need to automate this process.
If we know the gradient of our mae() function with respect to our parameters, a, b and c, then that means we know how adjusting a parameter will change the function. If, say, a has a negative gradient, then we know increasing a will decrease mae(). So we find the gradient of the parameters with respect to the loss function and adjust our parameters a bit in the opposite direction of the gradient sign.
To do this we need a function that will take the parameters as a single vector:
def quad_mae(params):
f = mk_quad(*params)
return mae(f(x), y)# testing it out
# should equal 2.4219
quad_mae([1.1, 1.1, 1.1])tensor(2.4219, dtype=torch.float64)# pick an arbitrary starting point for our parameters
abc = torch.tensor([1.1, 1.1, 1.1])
# tell pytorch to calculate its gradients
abc.requires_grad_()
# calculate loss
loss = quad_mae(abc)
losstensor(2.4219, dtype=torch.float64, grad_fn=<MeanBackward0>)# calculate gradients
loss.backward()
# view gradients
abc.gradtensor([-1.3529, -0.0316, -0.5000])# increase parameters to decrease loss based on gradient sign
with torch.no_grad():
abc -= abc.grad*0.01
loss = quad_mae(abc)
print(f'loss={loss:.2f}')loss=2.40The loss has gone down from 2.4219 to 2.40. We’re moving in the right direction.
The small number we multiply gradients by is called the learning rate and is the most important hyper-parameter to set when training a neural network.
# use a loop to do a few more iterations
for i in range(10):
loss = quad_mae(abc)
loss.backward()
with torch.no_grad(): abc -= abc.grad*0.01
print(f'step={i}; loss={loss:.2f}')step=0; loss=2.40
step=1; loss=2.36
step=2; loss=2.30
step=3; loss=2.21
step=4; loss=2.11
step=5; loss=1.98
step=6; loss=1.85
step=7; loss=1.72
step=8; loss=1.58
step=9; loss=1.46The loss continues to decrease. Here are our parameters and their gradients at this stage:
abctensor([1.9634, 1.1381, 1.4100], requires_grad=True)abc.gradtensor([-13.4260, -1.0842, -4.5000])A neural network can approximate any computable function, given enough parameters using two key steps:
- Matrix multiplication.
- The function \(max(x,0)\), which simply replaces all negative numbers with zero.
The combination of a linear function and \(max\) is called a rectified linear unit and can be written as:
def rectified_linear(m,b,x):
y = m*x+b
return torch.clip(y, 0.)# we can do the same thing using PyTorch
import torch.nn.functional as F
def rectified_linear2(m,b,x): return F.relu(m*x+b)
plot_function(partial(rectified_linear2, 1,1))Create an interactive ReLU:
@interact(m=1.5, b=1.5)
def plot_relu(m, b):
plot_function(partial(rectified_linear, m, b), ylim=(-1,4))Observe what happens when we add two ReLUs together:
def double_relu(m1,b1,m2,b2,x):
return rectified_linear(m1,b1,x) + rectified_linear(m2,b2,x)
@interact(m1=-1.5, b1=-1.5, m2=1.5, b2=1.5)
def plot_double_relu(m1, b1, m2, b2):
plot_function(partial(double_relu, m1,b1,m2,b2), ylim=(-1,6))Creating a triple ReLU function to fit our data:
def triple_relu(m1,b1,m2,b2,m3,b3,x):
return rectified_linear(m1,b1,x) + rectified_linear(m2,b2,x) + rectified_linear(m3,b3,x)
def mk_triple_relu(m1,b1,m2,b2,m3,b3): return partial(triple_relu, m1,b1,m2,b2,m3,b3)
@interact(m1=-1.5, b1=-1.5, m2=0.5, b2=0.5, m3=1.5, b3=1.5)
def plot_double_relu(m1, b1, m2, b2, m3, b3):
f = mk_triple_relu(m1,b1,m2,b2,m3,b3)
plt.scatter(x,y)
loss = mae(f(x), y)
plot_function(f, ylim=(-3,12), title=f"MAE: {loss:.2f}")This same approach can be extended to functions with 2, 3, or more parameters. Drawing squiggly lines through some points is literally all that deep learning does. The above steps will, given enough time and enough data, create (for example) an owl recognizer if you feed it enough owls and non-owls.
We can could do thousands of computations on a GPU instead of the above CPU computation. We can greatly reduce the amount of computation and data needed by using a convolution instead of a matrix multiplication. We could make things much faster if, instead of starting with random parameters, we start with parameters of someone else’s model that does something similar to what we want (transfer learning).
Gradient Descent with Microsoft Excel
Following the instructions in the fastai course lesson video, I’ve created a Microsoft Excel deep learning model here for the Titanic Kaggle data.
As shown in the course video, I trained three different models—linear regression, neural net (using SUMPRODUCT) and neural net (using MMULT). After running Microsoft Excel’s Solver, I got the final (different than video) mean loss for each model:
- linear: 0.14422715
- nnet: 0.14385956
- mmult: 0.14385956
The linear model loss in the video was about 0.10 and the neural net loss was about 0.08. So, my models didn’t do as well.
Book Notes
In this section, I’ll take notes while reading Chapter 4 in the fastai textbook.
Pixels: The Foundations of Computer Vision
- We’ll use the MNIST dataset for our experiments, which contains handwritten digits.
- MNIST is collected by the National Institute of Standards and Technology and collated into a machine learning dataset by Yann Lecun who used MNIST in 1998 in LeNet-5, the first computer system to demonstrate practically useful recognition of handwritten digits.
- We’ve seen that the only consisten trait among every fast.ai student who’s gone on to be a world-class practitioner is that they are all very tenacious.
- In this chapter we’ll create a model that can classify any image as a 3 or a 7.
from fastai.vision.all import *path = untar_data(URLs.MNIST_SAMPLE)# ls method added by fastai
# lists the count of items
path.ls()(#3) [Path('/root/.fastai/data/mnist_sample/labels.csv'),Path('/root/.fastai/data/mnist_sample/train'),Path('/root/.fastai/data/mnist_sample/valid')](path/'train').ls()(#2) [Path('/root/.fastai/data/mnist_sample/train/3'),Path('/root/.fastai/data/mnist_sample/train/7')]# 3 and 7 are the labels
threes = (path/'train'/'3').ls().sorted()
sevens = (path/'train'/'7').ls().sorted()
threes(#6131) [Path('/root/.fastai/data/mnist_sample/train/3/10.png'),Path('/root/.fastai/data/mnist_sample/train/3/10000.png'),Path('/root/.fastai/data/mnist_sample/train/3/10011.png'),Path('/root/.fastai/data/mnist_sample/train/3/10031.png'),Path('/root/.fastai/data/mnist_sample/train/3/10034.png'),Path('/root/.fastai/data/mnist_sample/train/3/10042.png'),Path('/root/.fastai/data/mnist_sample/train/3/10052.png'),Path('/root/.fastai/data/mnist_sample/train/3/1007.png'),Path('/root/.fastai/data/mnist_sample/train/3/10074.png'),Path('/root/.fastai/data/mnist_sample/train/3/10091.png')...]# the image is stored as numbers
array(im3)[4:10, 4:10]array([[ 0, 0, 0, 0, 0, 0],
[ 0, 0, 0, 0, 0, 29],
[ 0, 0, 0, 48, 166, 224],
[ 0, 93, 244, 249, 253, 187],
[ 0, 107, 253, 253, 230, 48],
[ 0, 3, 20, 20, 15, 0]], dtype=uint8)# same thing, but a PyTorch tensor
tensor(im3)[4:10, 4:10]tensor([[ 0, 0, 0, 0, 0, 0],
[ 0, 0, 0, 0, 0, 29],
[ 0, 0, 0, 48, 166, 224],
[ 0, 93, 244, 249, 253, 187],
[ 0, 107, 253, 253, 230, 48],
[ 0, 3, 20, 20, 15, 0]], dtype=torch.uint8)# use pandas.DataFrame to color code the array
im3_t = tensor(im3)
df = pd.DataFrame(im3_t[4:15, 4:22])
df.style.set_properties(**{'font-size': '6pt'}).background_gradient('Greys')| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 1 | 0 | 0 | 0 | 0 | 0 | 29 | 150 | 195 | 254 | 255 | 254 | 176 | 193 | 150 | 96 | 0 | 0 | 0 |
| 2 | 0 | 0 | 0 | 48 | 166 | 224 | 253 | 253 | 234 | 196 | 253 | 253 | 253 | 253 | 233 | 0 | 0 | 0 |
| 3 | 0 | 93 | 244 | 249 | 253 | 187 | 46 | 10 | 8 | 4 | 10 | 194 | 253 | 253 | 233 | 0 | 0 | 0 |
| 4 | 0 | 107 | 253 | 253 | 230 | 48 | 0 | 0 | 0 | 0 | 0 | 192 | 253 | 253 | 156 | 0 | 0 | 0 |
| 5 | 0 | 3 | 20 | 20 | 15 | 0 | 0 | 0 | 0 | 0 | 43 | 224 | 253 | 245 | 74 | 0 | 0 | 0 |
| 6 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 249 | 253 | 245 | 126 | 0 | 0 | 0 | 0 |
| 7 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 14 | 101 | 223 | 253 | 248 | 124 | 0 | 0 | 0 | 0 | 0 |
| 8 | 0 | 0 | 0 | 0 | 0 | 11 | 166 | 239 | 253 | 253 | 253 | 187 | 30 | 0 | 0 | 0 | 0 | 0 |
| 9 | 0 | 0 | 0 | 0 | 0 | 16 | 248 | 250 | 253 | 253 | 253 | 253 | 232 | 213 | 111 | 2 | 0 | 0 |
| 10 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 43 | 98 | 98 | 208 | 253 | 253 | 253 | 253 | 187 | 22 | 0 |
The background white pixels are stored a the number 0, black is the number 255, and shades of grey between the two. The entire image contains 28 pixels across and 28 pixels down for a total of 768 pixels.
How might a computer recognize these two digits?
Ideas:
3s and 7s have distinct features. A seven has generally two straight lines at different angles, a three as two sets of curves stacked on each other. The point where the two curves intersect could be a recognizable feature of the the digit three. The point where the two straight-ish lines intersect could be a recognizable feature of the digit seven. One feature of confusion could be handwritten threes with a straight line at the top, similar to a seven. Another feature of confusion could be a handwritten 3 with a straight-ish ending stroke at the bottom, matching a similar stroke of a 7.
First Try: Pixel Similarity
Idea: find the average pixel value for every pixel of the 3s, then do the same for the 7s. To classify an image, see which of the two ideal digits the image is most similar to.
Baseline: A simple model that you are confident should perform reasonably well. It should be simple to implement and easy to test, so that you can then test each of your improved ideas and make sure they are always better than your baseline. Without starting with a sensible baseline, it is difficult to know whether your super-fancy models are any good.
# list comprehension of all digit images
seven_tensors = [tensor(Image.open(o)) for o in sevens]
three_tensors = [tensor(Image.open(o)) for o in threes]
len(three_tensors), len(seven_tensors)(6131, 6265)For every pixel position, we want to compute the average over all the images of the intensity of that pixel. To do this, combine all the images in this list into a single three-dimensional tensor.
When images are floats, the pixel values are expected to be between 0 and 1.
stacked_sevens = torch.stack(seven_tensors).float()/255
stacked_threes = torch.stack(three_tensors).float()/255
stacked_threes.shapetorch.Size([6131, 28, 28])# the length of a tensor's shape is its rank
# rank is the number of axes and dimensions in a tensor
# shape is the size of each axis of a tensor
len(stacked_threes.shape)3# rank of a tensor
stacked_threes.ndim3We calculate the mean of all the image tensors by taking the mean along dimension 0 of our stacked, rank-3 tensor. This is the dimension that indexes over all the images.
mean3 = stacked_threes.mean(0)
mean3.shapetorch.Size([28, 28])This is the ideal number 3 based on the dataset. It’s saturated where all the images agree it should be saturated (much of the background, the intersection of the two curves, and top and bottom curve), but it becomes wispy and blurry where the images disagree.
How would I calculate how similar a particular image is to each of our ideal digits?
I would take the average of the absolute difference between each pixel’s intensity and the corresponding mean digit pixel intensity. The lower the average difference, the closer the digit is to the ideal digit.
L1 norm = Mean of the absolute value of differences.
Root mean squared error (RMSE) = square root of mean of the square of differences.
# L1 norm
dist_3_abs = (a_3 - mean3).abs().mean()
# RMSE
dist_3_sqr = ((a_3 - mean3)**2).mean().sqrt()
dist_3_abs, dist_3_sqr(tensor(0.1114), tensor(0.2021))# L1 norm
dist_7_abs = (a_3 - mean7).abs().mean()
# RMSE
dist_7_sqr = ((a_3 - mean7)**2).mean().sqrt()
dist_7_abs, dist_7_sqr(tensor(0.1586), tensor(0.3021))For both L1 norm and RMSE, the distance between the 3 and the “ideal” 3 is less than the distance to the ideal 7, so our simple model will give the right prediction in this case.
Both distances are provided in PyTorch:
F.l1_loss(a_3.float(), mean7), F.mse_loss(a_3, mean7).sqrt()(tensor(0.1586), tensor(0.3021))MSE = mean squared error.
MSE will penalize bigger mistakes more heavily (and be lenient with small mistakes) than L1 norm.
NumPy Arrays and PyTorch Tensors
A NumPy array is a multidimensional table of data with all items of the same type.
jagged array: nested arrays of different sizes.
If the items of the array are all of simple type such as integer or float, NumPy will store them as a compact C data structure in memory.
PyTorch tensors cannot be jagged. PyTorch tensors can live on the GPU. And can calculate their derivatives.
# creating arrays and tensors
data = [[1,2,3], [4,5,6]]
arr = array(data)
tns = tensor(data)
arrarray([[1, 2, 3],
[4, 5, 6]])tnstensor([[1, 2, 3],
[4, 5, 6]])# select a row
tns[1]tensor([4, 5, 6])# select a column
tns[:,1]tensor([2, 5])# slice
tns[1, 1:3]tensor([5, 6])# standard operators
tns + 1tensor([[2, 3, 4],
[5, 6, 7]])# tensor type
tns.type()'torch.LongTensor'# tensor changes type when needed
(tns * 1.5).type()'torch.FloatTensor'Computing Metrics Using Broadcasting
metric = a number that is calculated based on the predictions of our model and the correct labels in our dataset in order to tell us how good our model is.
Calculate the metric on the validation set.
valid_3_tens = torch.stack([tensor(Image.open(o)) for o in (path/'valid'/'3').ls()])
valid_3_tens = valid_3_tens.float()/255
valid_7_tens = torch.stack([tensor(Image.open(o)) for o in (path/'valid'/'7').ls()])
valid_7_tens = valid_7_tens.float()/255
valid_3_tens.shape, valid_7_tens.shape(torch.Size([1010, 28, 28]), torch.Size([1028, 28, 28]))# measure distance between image and ideal
def mnist_distance(a,b): return (a-b).abs().mean((-1,-2))
mnist_distance(a_3, mean3)tensor(0.1114)# calculate mnist_distance for digit 3 validation images
valid_3_dist = mnist_distance(valid_3_tens, mean3)
valid_3_dist, valid_3_dist.shape(tensor([0.1109, 0.1202, 0.1276, ..., 0.1357, 0.1262, 0.1157]),
torch.Size([1010]))PyTorch broadcasts mean3 to each of the 1010 valid_3_dist tensors in order to calculate the distance. It doesn’t actually copy mean3 1010 times. It does the whole calculation in C (or CUDA for GPU).
In mean((-1, -2)), the tuple (-1, -2) represents a range of axes. This tells PyTorch that we want to take the mean ranging over the values indexed by the last two axes of the tensor—the horizontal and the vertical dimensions of an image.
If the distance between the digit in question and the ideal 3 is less than the distance to the ideal 7, then it’s a 3:
def is_3(x): return mnist_distance(x, mean3) < mnist_distance(x, mean7)is_3(a_3), is_3(a_3).float()(tensor(True), tensor(1.))# full validation set---thanks to broadcasting
is_3(valid_3_tens)tensor([ True, True, True, ..., False, True, True])# calculate accuracy
accuracy_3s = is_3(valid_3_tens).float().mean()
accuracy_7s = (1 - is_3(valid_7_tens).float()).mean()
accuracy_3s, accuracy_7s, (accuracy_3s + accuracy_7s) / 2(tensor(0.9168), tensor(0.9854), tensor(0.9511))We are getting more than 90% accuracy on both 3s and 7s. But they are very different looking digits and we’re classifying only 2 out of 10 digits, so we need to make a better model.
Stochastic Gradient Descent
Arthur Samuel’s description of machine learning
Suppose we arrange for some automatic means of testing the effectiveness of any current weight assignment in terms of actual performance and provide a mechanism for altering the weight assignment so as to maximize the performance. We need not go into the details of such a procedure to see that it could be made entirely automatic and to see that a machine so programmed would “learn” from its experience.
Our pixel similarity approach doesn’t have any weight assignment, or any way of improving based on testing the effectiveness of a weight assignment. We can’t improve our pixel similarity approach.
We could look at each individual pixel and come up with a set of weights for each, such that the highest weights are associated with those pixels most likely to be black for a particular category. For example, pixels toward the bottom right are not very likely to be activate for a 7, so they should have a low weight for a 7, but ther are likely to be activated for an 8, so they should have a high weight for an 8. This can be represented as a function and set of weight values for each possible category, for instance, the probability of being the number 8:
def pr_eight(x,w) = (x*w).sum()X is the image, represented as a vector (with all the rows stacked up end to end into a single long line) and the weights are a vector W. We need some way to update the weights to make them a little bit better. We want to find the specific values for the vector W that cause the result of our function to be high for those images that are 8s and low for those images that are not. Searching for the best vector W is a way to search for the best function for recognizing 8s.
Steps required to turn this function into a machine learning classifier:
- Initialize the weights.
- For each image, use these weights to predict whether it appears to be a 3 or a 7.
- Based on these predictions, calculate how good the model is (its loss).
- Calculate the gradient, which measures for each weight how changing that weight would change the loss.
- Step (that is, change) all the weights based on that calculation.
- Go back to step 2 and repeat the process.
- Iterate until you decide to stop the training process (for instance, because the model is good enough or you don’t want to wait any longer).
Initialize: Initialize parameters to random values.
Loss: We need a function that will return a number that is small if the performance of the model is good (by convention).
Step: Gradients allow us to directly figure out in which direction and by roughly how much to change each weight.
Stop: Keep training until the accuracy of the model started getting worse or we ran out of time, or once the number of epochs we decided are complete.
Calculating Gradients
Create an example loss function:
def f(x): return x**2Pick a tensor value at which we want gradients:
xt = tensor(3.).requires_grad_()yt = f(xt)
yttensor(9., grad_fn=<PowBackward0>)Calculate gradients (backpropagation–during the backward pass of the network, as opposed to forward pass which is where the activations are calculated):
yt.backward()View the gradients:
xt.gradtensor(6.)The derivative of x**2 is 2*x. When x = 3 the derivative is 6, as calculated above.
Calculating vector gradients:
xt = tensor([3., 4., 10.]).requires_grad_()
xttensor([ 3., 4., 10.], requires_grad=True)Add sum to our function so it takes a vector and returns a scalar:
def f(x): return (x**2).sum()yt = f(xt)
yttensor(125., grad_fn=<SumBackward0>)yt.backward()
xt.gradtensor([ 6., 8., 20.])If the gradients are very large, that may suggest that we have more adjustments to do, whereas if they are very small, that may suggest that we are close to the optimal value.
Stepping with a Learning Rate
Deciding how to change our parameters based on the values of the gradients—multiplying the gradient by some small number called the learning rate (LR):
w -= w.grad * lrThis is knowns as stepping your parameters using an optimization step.
If you pick a learning rate too low, that can mean having to do a lot of steps. If you pick a learning rate too high, that’s even worse, because it can result in the loss getting worse. If the learning rate is too high it may also “bounce” around.
An End-to-End SGD Example
Example: measuring the speed of a roller coaster as it went over the top of a hump. It would start fast, get slower as it went up the hill, and speed up again going downhill.
time = torch.arange(0,20).float(); timetensor([ 0., 1., 2., 3., 4., 5., 6., 7., 8., 9., 10., 11., 12., 13.,
14., 15., 16., 17., 18., 19.])speed = torch.randn(20)*3 + 0.75*(time-9.5)**2 + 1
speedtensor([72.1328, 55.1778, 39.8417, 33.9289, 21.9506, 18.0992, 11.3346, 0.3637,
7.3242, 4.0297, 3.9236, 4.1486, 1.9496, 6.1447, 12.7890, 23.8966,
30.6053, 45.6052, 53.5180, 71.2243])We added a bit of random noise since measuring things manually isn’t precise.
What was the roller coaster’s speed? Using SGD, we can try to find a function that matches our observations. Guess that it will be a quadratic of the form a*(time**2) + (b*t) + c.
We want to distinguish clearly between the function’s input (the time when we are measuring the coaster’s speed) and its parameters (the values that define which quadratic we’re trying).
Collect parameters in one argument and separate t and params in the function’s signature:
def f(t, params):
a,b,c = params
return a*(t**2) + (b*t) + cDefine a loss function:
def mse(preds, targets): return ((preds-targets)**2).mean()Step 1: Initialize the parameters
params = torch.randn(3).requires_grad_()Step 2: Calculate the predictions
preds = f(time, params)Create a little function to see how close our predictions are to our targets:
def show_preds(preds, ax=None):
if ax is None: ax=plt.subplots()[1]
ax.scatter(time, speed)
ax.scatter(time, to_np(preds), color='red')
ax.set_ylim(-300,100)
show_preds(preds)Step 3: Calculate the loss
loss = mse(preds, speed)
losstensor(11895.1143, grad_fn=<MeanBackward0>)Step 4: Calculate the gradients
loss.backward()
params.gradtensor([-35554.0117, -2266.8909, -171.8540])paramstensor([-0.5364, 0.6043, 0.4822], requires_grad=True)Step 5: Step the weights
lr = 1e-5
params.data -= lr * params.grad.data
params.grad = NoneLet’s see if the loss has improved (it has) and take a look at the plot:
preds = f(time, params)
mse(preds, speed)tensor(2788.1594, grad_fn=<MeanBackward0>)Step 6: Repeat the process
def apply_step(params, prn=True):
preds = f(time, params)
loss = mse(preds, speed)
loss.backward()
params.data -= lr * params.grad.data
params.grad = None
if prn: print(loss.item())
return predsfor i in range(10): apply_step(params)2788.159423828125
1064.841552734375
738.7333984375
677.02001953125
665.3380737304688
663.1239013671875
662.7010498046875
662.6172485351562
662.59765625
662.5902709960938_, axs = plt.subplots(1,4,figsize=(12,3))
for ax in axs: show_preds(apply_step(params, False), ax)
plt.tight_layout()Step 7: Stop
We decided to stop after 10 epochs arbitrarily. In practice, we would watch the training and validation losses and our metrics to decide when to stop.
Summarizing Gradient Descent
- At the beginning, the weights of our model can be random (training from scratch) or come from a pretrained model (transfer learning).
- In both cases the model will need to learn better weights.
- Use a loss function to compare model outputs to targets.
- Change the weights to make the loss a bit lower by multiple gradients by the learning rate and subtracting from the parameters.
- Iterate until you have reached the lowest loss and then stop.
The MNIST Loss Function
Concatenate the images into a single tensor. view changes the shape of a tensor without changing its contents. -1 is a special parameter to view that means “make this axis as big as necessary to fit all the data”.
train_x = torch.cat([stacked_threes, stacked_sevens]).view(-1, 28*28)Use the label 1 for 3s and 0 for 7s. Unsqueeze adds a dimension of size one.
train_y = tensor([1]*len(threes) + [0]*len(sevens)).unsqueeze(1)
train_x.shape, train_y.shape(torch.Size([12396, 784]), torch.Size([12396, 1]))PyTorch Dataset is required to return a tuple of (x,y) when indexed.
dset = list(zip(train_x, train_y))
x,y = dset[0]
x.shape,y(torch.Size([784]), tensor([1]))Prepare the validation dataset:
valid_x = torch.cat([valid_3_tens, valid_7_tens]).view(-1, 28*28)
valid_y = tensor([1]*len(valid_3_tens) + [0]*len(valid_7_tens)).unsqueeze(1)
valid_dset = list(zip(valid_x, valid_y))
x,y = valid_dset[0]
x.shape, y(torch.Size([784]), tensor([1]))Step 1: Initialize the parameters
We need an initially random weight for every pixel.
def init_params(size, std=1.0): return (torch.randn(size)*std).requires_grad_()weights = init_params((28*28,1))
weights.shapetorch.Size([784, 1])\(y = wx + b\).
We created w (weights) now we need to create b (intercept or bias):
bias = init_params(1)
biastensor([-0.0313], requires_grad=True)Step 2: Calculate the predictions
Prediction for one image
(train_x[0] * weights.T).sum() + biastensor([0.5128], grad_fn=<AddBackward0>)In Python, matrix multiplication is represetend with the @ operator:
def linear1(xb): return xb@weights + bias
preds = linear1(train_x)
predstensor([[ 0.5128],
[-3.8324],
[ 4.9791],
...,
[ 3.0790],
[ 4.1521],
[ 0.3523]], grad_fn=<AddBackward0>)To decide if an output represents a 3 or a 7, we can just check whether it’s greater than 0:
corrects = (preds>0.0).float() == train_y
correctstensor([[ True],
[False],
[ True],
...,
[False],
[False],
[False]])corrects.float().mean().item()0.38964182138442993Step 3: Calculate the loss
A very small change in the value of a weight will often not change the accuracy at all, and thus the gradient is 0 almost everywhere. It’s not useful to use accuracy as a loss function.
We need a loss function that when our weights result in slightly better predictions, gives us a slightly better loss.
In this case, what does “slightly better prediction mean”: if the correct answer is 3 (1), the score is a little higher, or if the correct answer is a 7 (0), the score is a little lower.
The loss function receives not the images themselves, but the predictions from the model.
The loss function will measure how distant each prediction is from 1 (if it should be 1) and how distant it is from 0 (if it should be 0) and then it will take the mean of all those distances.
def mnist_loss(predictions, targets):
return torch.where(targets==1, 1-predictions, predictions).mean()Try it out with sample predictions and targets:
trgts = tensor([1,0,1])
prds = tensor([0.9, 0.4, 0.2])
torch.where(trgts==1, 1-prds, prds)tensor([0.1000, 0.4000, 0.8000])This function returns a lower number when predictions are more accurate, when accurate predictions are more confident and when inaccurate predictions are less confident.
Since we need a scalar for the final loss, mnist_loss takes the mean of the previous tensor:
mnist_loss(prds, trgts)tensor(0.4333)mnist_loss assumes that predictions are between 0 and 1. We need to ensure that, using sigmoid, which always outputs a number between 0 and 1:
def sigmoid(x): return 1/(1+torch.exp(-x))It’s also a smooth curve that only goes up, which makes it easier for SGD to find meaningful gradients. Update mnist+loss to first apply sigmoid to the inputs:
def mnist_loss(predictions, targets):
predictions = predictions.sigmoid()
return torch.where(targets==1, 1-predictions, predictions).mean()We already had a metric, which was overall accuracy. So why did we define a loss?
To drive automated learning, the loss must be a function that has a meaningful derivative. It can’t have big flat sections and large jumps, but instead must be reasonably smooth. This is why we designed a loss function that would respond to small changes in confidence level.
The loss function is calculated for each item in our dataset, and then at the end of an epoch, the loss values are all averaged and the overall mean is reported for the epoch.
It is important that we focus on metrics, rather than the loss, when judging the performance of a model.
SGD and Mini-Batches
The optimization step: change or update the weights based on the gradients.
To take an optimization step, we need to calculate the loss over one or more data items. Calculating the loss for the whole dataset would take a long time, calculating it for a single item would not use much information so it would result in an imprecise and unstable gradient.
Calculate the average loss for a few data items at a time (mini-batch). The number of data items in the mini-batch is called the batch-size.
A larger batch size means you will get a more accurate and stable estimate of your dataset’s gradients from the loss function, but it will take longer and you will process fewer mini-batches per epoch. Using batches of data works well for GPUs, but give the GPU too many items at once and it will run out of memory.
We get better generalization if we can vary things during training (like performing data augmentation). One simple and effective thing we can vary is what data items we put in each mini-batch. Randomly shuffly the dataset before we create mini-batches. The DataLoader will do the shuffling and mini-batch collation for you:
coll = range(15)
dl = DataLoader(coll, batch_size=5, shuffle=True)
list(dl)[tensor([10, 3, 8, 11, 0]),
tensor([6, 1, 7, 9, 4]),
tensor([12, 13, 5, 2, 14])]For training, we want a collection containing independent and dependent variables. A Dataset in PyTorch is a collection containing tuples of independent and dependent variables.
ds = L(enumerate(string.ascii_lowercase))
ds(#26) [(0, 'a'),(1, 'b'),(2, 'c'),(3, 'd'),(4, 'e'),(5, 'f'),(6, 'g'),(7, 'h'),(8, 'i'),(9, 'j')...]list(enumerate(string.ascii_lowercase))[:5][(0, 'a'), (1, 'b'), (2, 'c'), (3, 'd'), (4, 'e')]When we pass a Dataset to a Dataloader we will get back many batches that are themselves tuples of tensors representing batches of independent and dependent variables:
dl = DataLoader(ds, batch_size=6, shuffle=True)
list(dl)[(tensor([24, 2, 4, 8, 9, 13]), ('y', 'c', 'e', 'i', 'j', 'n')),
(tensor([23, 17, 6, 14, 25, 18]), ('x', 'r', 'g', 'o', 'z', 's')),
(tensor([22, 5, 7, 20, 3, 19]), ('w', 'f', 'h', 'u', 'd', 't')),
(tensor([ 0, 21, 12, 1, 16, 10]), ('a', 'v', 'm', 'b', 'q', 'k')),
(tensor([11, 15]), ('l', 'p'))]Putting It All Together
In code, the process will be implemented something like this for each epoch:
for x,y in dl:
# calculate predictions
pred = model(x)
# calculate the loss
loss = loss_func(pred, y)
# calculate the gradients
loss.backward()
# step the weights
parameters -= parameters.grad * lrStep 1: Initialize the parameters
weights = init_params((28*28, 1))
bias = init_params(1)A DataLoader can be created from a Dataset:
dl = DataLoader(dset, batch_size=256)
xb,yb = first(dl)
xb.shape, yb.shape(torch.Size([256, 784]), torch.Size([256, 1]))Do the same for the validation set:
valid_dl = DataLoader(valid_dset, batch_size=256)Create a mini-batch of size 4 for testing:
batch = train_x[:4]
batch.shapetorch.Size([4, 784])preds = linear1(batch)
predstensor([[10.4546],
[ 9.4603],
[-0.2426],
[ 6.7868]], grad_fn=<AddBackward0>)loss = mnist_loss(preds, train_y[:4])
losstensor(0.1404, grad_fn=<MeanBackward0>)Step 4: Calculate the gradients
loss.backward()
weights.grad.shape, weights.grad.mean(), bias.grad(torch.Size([784, 1]), tensor(-0.0089), tensor([-0.0619]))Create a function to calculate gradients:
def calc_grad(xb, yb, model):
preds = model(xb)
loss = mnist_loss(preds, yb)
loss.backward()Test it:
calc_grad(batch, train_y[:4], linear1)
weights.grad.mean(), bias.grad(tensor(-0.0178), tensor([-0.1238]))Look what happens when we call it again:
calc_grad(batch, train_y[:4], linear1)
weights.grad.mean(), bias.grad(tensor(-0.0267), tensor([-0.1857]))The gradients have changed. loss.backward adds the gradients of loss to any gradients that are currently stored. So we have to set the current gradients to 0 first:
weights.grad.zero_()
bias.grad.zero_();Methods in PyTorch whose names end in an underscore modify their objects in place.
Step 5: Step the weights
When we update the weights and biases based on the gradient and learning rate, we have to tell PyTorch not to take the gradient of this step. If we assign to the data attribute of a tensor, PyTorch will not take the gradient of that step. Here’s our basic training loop for an epoch:
def train_epoch(model, lr, params):
for xb,yb in dl:
calc_grad(xb, yb, model)
for p in params:
p.data -= p.grad*lr
p.grad.zero_()We want to check how we’re doing by looking at the accuracy of the validation set. To decide if an output represents a 3 (1) or a 7 (0) we can just check whether the prediction is greater than 0.
preds, train_y[:4](tensor([[10.4546],
[ 9.4603],
[-0.2426],
[ 6.7868]], grad_fn=<AddBackward0>),
tensor([[1],
[1],
[1],
[1]]))(preds>0.0).float() == train_y[:4]tensor([[ True],
[ True],
[False],
[ True]])# if preds is greater than 0 and the label is 1 -> correct 3 prediction
# if preds is not greater than 0 and the label is 0 -> correct 7 prediction
True == 1, False == 0(True, True)Create a function to calculate validation accuracy:
def batch_accuracy(xb, yb):
preds = xb.sigmoid()
correct = (preds>0.5) == yb
return correct.float().mean()batch_accuracy(linear1(batch), train_y[:4])tensor(0.7500)Put the batches back together:
def validate_epoch(model):
accs = [batch_accuracy(model(xb), yb) for xb,yb in valid_dl]
return round(torch.stack(accs).mean().item(), 4)Starting point accuracy:
validate_epoch(linear1)0.5703Let’s train for 1 epoch and see if the accuracy improves:
lr = 1.
params = weights, bias
train_epoch(linear1, lr, params)
validate_epoch(linear1)0.6928Step 6: Repeat the process
Then do a few more:
for i in range(20):
train_epoch(linear1, lr, params)
print(validate_epoch(linear1), end = ' ')0.852 0.9061 0.931 0.9418 0.9477 0.9569 0.9584 0.9594 0.9599 0.9633 0.9647 0.9652 0.9657 0.9662 0.9672 0.9677 0.9687 0.9696 0.9701 0.9696 We’re already about at the same accuracy as our “pixel similarity” approach.
Creating an Optimizer
Replace our linear function with PyTorch’s nn.Lienar module. A module is an object of a class that inherits from the PyTorch nn.Module class, and behaves identically to standard Python functions in that you can call them using parentheses and they will return the activations of a model.
nn.Linear does the same thing as our init_params and linear together. It contains both weights and biases in a single class:
linear_model = nn.Linear(28*28, 1)Every PyTorch module knows what parameters it has that can be trained; they are available through the parameters method:
w,b = linear_model.parameters()
w.shape, b.shape(torch.Size([1, 784]), torch.Size([1]))We can use this information to create an optimizer:
class BasicOptim:
def __init__(self,params,lr): self.params,self.lr = list(params),lr
def step(self, *args, **kwargs):
for p in self.params: p.data -= p.grad.data * self.lr
def zero_grad(self, *args, **kwargs):
for p in self.params: p.grad = NoneWe can create our optimizer by passing in the model’s parameters:
opt = BasicOptim(linear_model.parameters(), lr)Simplify our training loop:
def train_epoch(model):
for xb,yb in dl:
# calculate the gradients
calc_grad(xb,yb,model)
# step the weights
opt.step()
opt.zero_grad()Our validation function doesn’t need to change at all:
validate_epoch(linear_model)0.3985Put our training loop in a function:
def train_model(model, epochs):
for i in range(epochs):
train_epoch(model)
print(validate_epoch(model), end=' ')Similar results as the previous training:
train_model(linear_model, 20)0.4932 0.7959 0.8506 0.9136 0.9341 0.9492 0.9556 0.9629 0.9658 0.9683 0.9702 0.9717 0.9741 0.9746 0.9761 0.9766 0.9775 0.978 0.9785 0.979 fastai provides the SGD class that by default does the same thing as our BasicOptim:
linear_model = nn.Linear(28*28, 1)
opt = SGD(linear_model.parameters(), lr)
train_model(linear_model, 20)0.4932 0.8735 0.8174 0.9082 0.9331 0.9468 0.9546 0.9614 0.9653 0.9668 0.9692 0.9727 0.9736 0.9751 0.9756 0.9761 0.9775 0.978 0.978 0.9785 fastai provides Learner.fit which we can use instead of train_model. To create a Learner we first need to create a DataLoaders, by passing our training and validation DataLoaders:
dls = DataLoaders(dl, valid_dl)To create a Learner without using an application such as cnn_learner we need to pass in all the elements that we’ve created in this chapter: the DataLoaders, the model, the optimization function (which will be passed the parameters), the loss function, and optionally any metrics to print:
learn = Learner(dls, nn.Linear(28*28, 1), opt_func=SGD, loss_func=mnist_loss, metrics=batch_accuracy)learn.fit(10, lr=lr)| epoch | train_loss | valid_loss | batch_accuracy | time |
|---|---|---|---|---|
| 0 | 0.636474 | 0.503518 | 0.495584 | 00:00 |
| 1 | 0.550751 | 0.189374 | 0.840530 | 00:00 |
| 2 | 0.201501 | 0.178350 | 0.839549 | 00:00 |
| 3 | 0.087588 | 0.105257 | 0.912659 | 00:00 |
| 4 | 0.045719 | 0.076968 | 0.933759 | 00:00 |
| 5 | 0.029454 | 0.061683 | 0.947498 | 00:00 |
| 6 | 0.022817 | 0.052156 | 0.954367 | 00:00 |
| 7 | 0.019893 | 0.045825 | 0.962709 | 00:00 |
| 8 | 0.018424 | 0.041383 | 0.965653 | 00:00 |
| 9 | 0.017549 | 0.038113 | 0.967125 | 00:00 |
Adding a Nonlinearity
Adding a nonlinearity between two linear classifiers givs us a neural network.
def simple_net(xb):
res = xb@w1 + b1
res = res.max(tensor(0.0))
res = res@w2 + b2
return res# initialize weights
w1 = init_params((28*28, 30))
b1 = init_params(30)
w2 = init_params((30,1))
b2 = init_params(1)w1 has 30 output activations which means w2 must have 30 input activations so that they match. 30 output activations means that the first layer can construct 30 different features, each representing a different mix of pixels. You can change that 30 to anything you like to make the model more or less complex.
res.max(tensor(0.0)) is called a rectified linear unit or ReLU. It replaces every negative number with a zero.
We need a nonlinearity becauase a series of any number of linear layers in a row can be replaced with a single linear layer with a different set of parameters.
The neural net can solve any computable problem to an arbitrarily high level of accuracy if you can find the right parameters w1 and w2 and if you make the matrices big enough.
We can replace our function with PyTorch:
simple_net = nn.Sequential(
nn.Linear(28*28, 30),
nn.ReLU(),
nn.Linear(30,1)
)nn.Sequential create a modeule that will call each of the listed layers or functions in turn. When using nn.Sequential PyTorch requires us to use the module version (nn.ReLU) and not the function version (F.relu). Modules are classes so you have to instantiate them.
learn = Learner(dls, simple_net, opt_func=SGD,
loss_func=mnist_loss, metrics=batch_accuracy)learn.fit(40, 0.1)| epoch | train_loss | valid_loss | batch_accuracy | time |
|---|---|---|---|---|
| 0 | 0.363529 | 0.409795 | 0.505888 | 00:00 |
| 1 | 0.165949 | 0.239534 | 0.792934 | 00:00 |
| 2 | 0.089140 | 0.117148 | 0.913150 | 00:00 |
| 3 | 0.056798 | 0.078107 | 0.941119 | 00:00 |
| 4 | 0.042071 | 0.060734 | 0.957311 | 00:00 |
| 5 | 0.034718 | 0.051121 | 0.962218 | 00:00 |
| 6 | 0.030605 | 0.045103 | 0.964181 | 00:00 |
| 7 | 0.027994 | 0.040995 | 0.966143 | 00:00 |
| 8 | 0.026145 | 0.037990 | 0.969087 | 00:00 |
| 9 | 0.024728 | 0.035686 | 0.970559 | 00:00 |
| 10 | 0.023585 | 0.033853 | 0.972522 | 00:00 |
| 11 | 0.022634 | 0.032346 | 0.973994 | 00:00 |
| 12 | 0.021826 | 0.031080 | 0.975466 | 00:00 |
| 13 | 0.021127 | 0.029996 | 0.976448 | 00:00 |
| 14 | 0.020514 | 0.029053 | 0.975957 | 00:00 |
| 15 | 0.019972 | 0.028221 | 0.976448 | 00:00 |
| 16 | 0.019488 | 0.027481 | 0.977920 | 00:00 |
| 17 | 0.019051 | 0.026818 | 0.978410 | 00:00 |
| 18 | 0.018654 | 0.026219 | 0.978410 | 00:00 |
| 19 | 0.018291 | 0.025677 | 0.978901 | 00:00 |
| 20 | 0.017958 | 0.025181 | 0.978901 | 00:00 |
| 21 | 0.017650 | 0.024727 | 0.980373 | 00:00 |
| 22 | 0.017363 | 0.024310 | 0.980864 | 00:00 |
| 23 | 0.017096 | 0.023925 | 0.980864 | 00:00 |
| 24 | 0.016846 | 0.023570 | 0.981845 | 00:00 |
| 25 | 0.016610 | 0.023241 | 0.982336 | 00:00 |
| 26 | 0.016389 | 0.022935 | 0.982336 | 00:00 |
| 27 | 0.016179 | 0.022652 | 0.982826 | 00:00 |
| 28 | 0.015980 | 0.022388 | 0.982826 | 00:00 |
| 29 | 0.015791 | 0.022142 | 0.982826 | 00:00 |
| 30 | 0.015611 | 0.021913 | 0.983317 | 00:00 |
| 31 | 0.015440 | 0.021700 | 0.983317 | 00:00 |
| 32 | 0.015276 | 0.021500 | 0.983317 | 00:00 |
| 33 | 0.015120 | 0.021313 | 0.983317 | 00:00 |
| 34 | 0.014969 | 0.021137 | 0.983317 | 00:00 |
| 35 | 0.014825 | 0.020972 | 0.983317 | 00:00 |
| 36 | 0.014686 | 0.020817 | 0.982826 | 00:00 |
| 37 | 0.014553 | 0.020671 | 0.982826 | 00:00 |
| 38 | 0.014424 | 0.020532 | 0.982826 | 00:00 |
| 39 | 0.014300 | 0.020401 | 0.982826 | 00:00 |
You can view the training process in learn.recorder:
View the final accuracy:
learn.recorder.values[-1][2]0.982826292514801At this point we have:
- A function that can solve any problem to any level of accuracy (the neural network) given the correct set of parameters.
- A way to find the best set of parameters for any function (stochastic gradient descent).
Going Deeper
We can add as many layers in our neural network as we want, as long as we add a nonlinearity between each pair of linear layers.
The deeper the model gets, the harder it is to optimize the parameters.
With a deeper model (one with more layers) we do not need to use as many parameters. We can use smaller matrices with more layers and get better results than we would get with larger matrices and few layers.
In the 1990s what held back the field for years was that so few researchers were experimenting with more than one nonlinearity.
Training an 18-layer model:
dls = ImageDataLoaders.from_folder(path)
learn = cnn_learner(dls, resnet18, pretrained=False,
loss_func=F.cross_entropy, metrics=accuracy)
learn.fit_one_cycle(1, 0.1)/usr/local/lib/python3.10/dist-packages/fastai/vision/learner.py:288: UserWarning: `cnn_learner` has been renamed to `vision_learner` -- please update your code
warn("`cnn_learner` has been renamed to `vision_learner` -- please update your code")
/usr/local/lib/python3.10/dist-packages/torchvision/models/_utils.py:208: UserWarning: The parameter 'pretrained' is deprecated since 0.13 and may be removed in the future, please use 'weights' instead.
warnings.warn(
/usr/local/lib/python3.10/dist-packages/torchvision/models/_utils.py:223: UserWarning: Arguments other than a weight enum or `None` for 'weights' are deprecated since 0.13 and may be removed in the future. The current behavior is equivalent to passing `weights=None`.
warnings.warn(msg)| epoch | train_loss | valid_loss | accuracy | time |
|---|---|---|---|---|
| 0 | 0.098852 | 0.014919 | 0.996075 | 02:01 |
Jargon Recap
Activations: Numbers that are calculated (both by linear and nonlinear layers)
Parameters: Numbers that are randomly initialized and optimized (that is, the numbers that define the model).
Part of becoming a good deep learning practitioner is getting used to the idea of looking at your activations and parameters, and plotting the and testing whether they are behaving correctly.
Activations and parameters are all contained in tensors. The number of dimensions of a tensor is its rank.
A neural network contains a number of layers. Each layer is either linear or nonlinear. We generally alternate between these two kinds of layers in a neural network. Sometimes a nonlinearity is referred to as an activation function.
Key concepts related to SGD:
| Term | Meaning |
|---|---|
| ReLU | Function that returns 0 for negative numbers and doesn’t change positive numbers. |
| Mini-batch | A small group of inputs and labels gathered together in two arrays. A gradient descent is updated on this batch (rather than a whole epoch). |
| Forward pass | Applying the model to some input and computing the predictions. |
| Loss | A value that represents how well or badly our model is doing. |
| Gradient | The derivative of the loss with respect to some parameter of the model. |
| Backward pass | Computing the gradients of the loss with respect to all model parameters. |
| Gradient descent | Taking a step in the direction opposite to the gradients to make the model parameters a little bit better. |
| Learning rate | The size of the step we take when applying SGD to update the parameters of the model. |
Questionnaire
1. How is a grayscale image represented on a computer? How about a color image?
Grayscale image pixels can be 0 (black) to 255 (white). Color image pixels have three values (Red, Green, Blue) where each value can be from 0 to 255.
2. How are the files and folders in the MNIST_SAMPLE dataset structured? Why?
path.ls()(#3) [Path('/root/.fastai/data/mnist_sample/labels.csv'),Path('/root/.fastai/data/mnist_sample/train'),Path('/root/.fastai/data/mnist_sample/valid')]MNIST_SAMPLE path has a labels.csv file, a train folder, and a valid folder.
(path/'train').ls()(#2) [Path('/root/.fastai/data/mnist_sample/train/3'),Path('/root/.fastai/data/mnist_sample/train/7')]The train folder has a 3 and a 7 folder, each which contains training images.
(path/'valid').ls()(#2) [Path('/root/.fastai/data/mnist_sample/valid/3'),Path('/root/.fastai/data/mnist_sample/valid/7')]The valid folder contains a 3 and a 7 folder, each containing validation set images.
3. Explain how the “pixel similarity” approach to classifying digits works.
Pixel similarity works by calculating the absolute mean difference (L1 norm) between each image and the mean digit 3, and averaging the classification (if the absolute mean difference between the image and the ideal 3 is less than the absolute mean difference between the image and the ideal 7, it’s classified as a 3) across all images of each digit’s validation set as the accuracy of the model.
4. What is list comprehension? Create one now that selects odd numbers from a list and doubles them.
List comprehension is syntax for creating a new list based on another sequence or iterable (docs)
# for each element in range(10)
# if the modulo of the element and 2 is not 0
# double the element's value and store in this new list
doubled_odds = [2*elem for elem in range(10) if elem % 2 != 0]
doubled_odds[2, 6, 10, 14, 18]5. What is a rank-3 tensor?
A rank-3 tensor is a “cube” (3-dimensional tensor).
6. What is the difference between tensor rank and shape? How do you get the rank from the shape?
Tensor rank is the number of dimensions of the tensor. Tensor shape is the number of elements in each dimension. The following tensor is a 2-dimensional tensor with rank 2, the shape of which is 3 elements by 2 elements.
a_tensor = tensor([[1,3], [4,5], [5,6]])
# dim == rank
a_tensor.dim(), a_tensor.shape(2, torch.Size([3, 2]))7. What are RMSE and L1 norm?
RMSE = Root Mean Squared Error: The square root of the mean of squared differences between two sets of values.
L1 norm = mean absolute difference: the mean of the absolute value of differences between two sets of values.
8. How can you apply a calculation on thousands of numbers at once, many thousands of times faster than a Python loop?
You can do so by using tensors on a GPU.
9. Create a 3x3 tensor or array containing the numbers from 1 to 9. Double it. Select the bottom four numbers.
a_tensor = tensor([[1,2,3], [4,5,6], [7,8,9]])
a_tensortensor([[1, 2, 3],
[4, 5, 6],
[7, 8, 9]])a_tensor = 2 * a_tensor
a_tensortensor([[ 2, 4, 6],
[ 8, 10, 12],
[14, 16, 18]])a_tensor.view(-1, 9)[0,-4:]tensor([12, 14, 16, 18])10. What is broadcasting? Broadcasting is when a tensor of smaller rank (or a scalar) is expanded so that you can perform an operation between it and a tensor of larger rank. Broadcasting makes it so that the two operands have the same rank.
a_tensor + tensor([1,2,3])tensor([[ 3, 6, 9],
[ 9, 12, 15],
[15, 18, 21]])- Are metrics generally calculated using the training set or the validation set? Why?
Metrics are calculated on the validation set because since that is the data the model does not see during training, the metric tells you how your model performs on data it hasn’t seen before.
12. What is SGD?
SGD is Stochastic Gradient Descent, an automated process where a model learns the right parameters needed to solve problems like image classification. The randomly (from scratch) or pretrained (transfer learning) parameters are updated using their gradients with respect to the loss and the learning rate. Metrics like the accuracy measure how well the model is performing.
13. Why does SGD use mini-batches?
One reason is to utilize the ability of a GPU to process a lot of data at once.
Another reason is that calculating the loss one image at a time leads to an unstable loss function whereas calculating the loss on the entire dataset takes too long. Mini-batches fall in between these two extremes.
14. What are the seven steps in SGD for machine learning?
- Initialize the weights.
- Calculate the predictions.
- Calculate the loss.
- Calculate gradients.
- Step the weights.
- Repeat the process.
- Stop.
15. How do we initialize the weights in a model?
Either randomly (if training from scratch) or using pretrained weights (if transfer learning from an existing model like resnet18).
16. What is loss?
A machine-friendly way to measure how well (or badly) the model is performing. The model is learning to step the weights in order to decrease the loss.
17. Why can’t we always use a high learning rate?
Because we risk overshooting the minimum loss (getting stuck back and forth between the two sides of the parabola) or diverging (resulting in larger losses each step).
18. What is a gradient?
The rate of change or derivative of one variable with respect to another variable. In our case, gradients are the ratio of change in loss to change in parameter at one point.
19. Do you need to know how to calculate gradients yourself?
Nope! Although you should understand the basic concept of derivatives. PyTorch calculates gradients with the .backward method.
20. Why can’t we use accuracy as a loss function?
Because small changes in predictions do not result in small changes in accuracy. Accuracy drastically jumps (from 0 to 1 in our MNIST_SAMPLE example) at one point, with 0 slope elsewhere. We want a smooth function where you can calculate non-zero and non-infinite derivatives everywhere.
21. Draw the sigmoid function. What is special about its shape?
The sigmoid function outputs between 0 and 1 for input values going from -inf to +inf. It also has a smooth positive slope everywhere so it’s easy to take the derivate.
22. What is the difference between a loss function and a metric?
The loss function is a machine-friendly way to measure the performance of the model while a metric is a human-friendly way to do the same.
The purpose of the loss function is to provide a smooth function to take derivates over so the training system can change the weights little by little towards the optimum.
The purpose of the metric is to inform the human how well or badly the model is learning during training.
23. What is the function to calculate new weights using a learning rate?
In code, the function is:
parameters.data -= parameters.grad * lr
The new weights are stepped incrementally in the opposite direction of the gradients. If the gradient is negative, the weights will be increased. If the gradient is positive, the weights will be decreased.
24. What does the DataLoader class do?
The DataLoader class prepares training and validation batches and feeds them to the GPU during training. It also performs any necessary item_tfms or batch_tfms to the data.
25. Write pseudocode showing the basic steps taken in each epoch for SGD.
def train_epoch(model):
# calculate predictions
preds = model(xb)
# calculate the loss
loss = loss_func(preds, targets)
# calculate gradients
loss.backward()
# step the weights
params.data -= params.grad * lr
# reset the gradients
params.zero_grad_()
# calculate accuracy
acc = tensor([accuracy for each batch]).mean()- Create a function that, if passed two arguments
[1, 2, 3, 4]and'abcd', returns[(1, 'a'), (2, 'b'), (3, 'c'), (4, 'd')]. What is special about that output data structure?
def zipped_tuples(x, y): return list(zip(x,y))zipped_tuples([1,2,3,4], 'abcd')[(1, 'a'), (2, 'b'), (3, 'c'), (4, 'd')]The output data structure is the same structure as the PyTorch Dataset.
27. What does view do in PyTorch?
view changes the rank and shape of the tensor.
tensor([1,2,3],[4,5,6]).view(3,2)tensor([[1, 2],
[3, 4],
[5, 6]])tensor([1,2,3],[4,5,6]).view(6)tensor([1, 2, 3, 4, 5, 6])28. What are the bias parameters in a neural network? Why do we need them?
The bias parameters are the intercept \(b\) in the function \(y = wx + b\). We need them for situations where the inputs are 0 (since \(w*0 = 0\)). Bias also helps to create a more flexible function (source).
29. What does the @ operator do in Python?
Matrix multiplication.
v1 = tensor([1,2,3])
v2 = tensor([4,5,6])
v1 @ v2tensor(32)30. What does the backward method do?
Calculate the gradients of the loss function with respect to the parameters.
31. Why do we have to zero the gradients?
Each time you call .backward PyTorch will add the new gradients to the current gradients, so we need to zero the gradients to prevent them from accumulating.
32. What information do we have to pass to Learner?
Reference:
Learner(dls, simple_net, opt_func=SGD,
loss_func=mnist_loss, metrics=batch_accuracy)We pass to the Learner:
DataLoaderscontaining training and validation sets.- The model we want to train.
- An optimizer function.
- A loss function.
- Any metrics we want calculated.
33. Show Python or pseudocode for the basic steps of a training loop.
See #25.
34. What is ReLU? Draw a plot for it for values from -2 to +2.
ReLU is Rectified Linear Unit. It’s a function where if the inputs are negative, they are set to zero, and if the inputs are positive, they are kept as is.
35. What is an activation function?
An activation function is the function that produces our predictions (in our case, a neural net with linear and nonlinear layers). Sometimes the ReLU is referred to as the activation function.
36. What’s the difference between F.relu and nn.ReLU?
F.relu is a function whereas nn.ReLU is a class that needs to be instantiated.
37. The universal approximation theorem shows that any function can be approximated as closely as needed using just one nonlinearity. So why wo we normally use more?
Using more layers results in more accurate models.
Further Research
Since this lesson’s Further Research was so intensive, I decided to create separate blog posts for each one:
Lesson 4: Natural Language (NLP)
As recommended at the end of the lesson 3 video, I will read + run through the code from Jeremy’s notebook Getting started with NLP for absolute beginners before starting lesson 4.
In this notebook we’ll see how to solve the Patent Phrase Matching problem by treating it as a classification task, by representing it in a very similar way to that shown above.
Notebook Exercise: Getting started with NLP for absolute beginners
Download the Data
!pip install kaggle! pip install -q datasets! pip install transformers[sentencepiece]!pip install accelerate -U# for working with paths in Python, I recommend using `pathlib.Path`
from pathlib import Path
cred_path = Path('~/.kaggle/kaggle.json').expanduser()
if not cred_path.exists():
cred_path.parent.mkdir(exist_ok=True)
cred_path.write_text(creds)
cred_path.chmod(0o600)path = Path('us-patent-phrase-to-phrase-matching')import zipfile,kaggle
kaggle.api.competition_download_cli(str(path))
zipfile.ZipFile(f'{path}.zip').extractall(path)Downloading us-patent-phrase-to-phrase-matching.zip to /content100%|██████████| 682k/682k [00:00<00:00, 750kB/s]!ls {path}sample_submission.csv test.csv train.csvView the Data
import pandas as pddf = pd.read_csv(path/'train.csv')df| id | anchor | target | context | score | |
|---|---|---|---|---|---|
| 0 | 37d61fd2272659b1 | abatement | abatement of pollution | A47 | 0.50 |
| 1 | 7b9652b17b68b7a4 | abatement | act of abating | A47 | 0.75 |
| 2 | 36d72442aefd8232 | abatement | active catalyst | A47 | 0.25 |
| 3 | 5296b0c19e1ce60e | abatement | eliminating process | A47 | 0.50 |
| 4 | 54c1e3b9184cb5b6 | abatement | forest region | A47 | 0.00 |
| ... | ... | ... | ... | ... | ... |
| 36468 | 8e1386cbefd7f245 | wood article | wooden article | B44 | 1.00 |
| 36469 | 42d9e032d1cd3242 | wood article | wooden box | B44 | 0.50 |
| 36470 | 208654ccb9e14fa3 | wood article | wooden handle | B44 | 0.50 |
| 36471 | 756ec035e694722b | wood article | wooden material | B44 | 0.75 |
| 36472 | 8d135da0b55b8c88 | wood article | wooden substrate | B44 | 0.50 |
36473 rows × 5 columns
df.describe(include='object')| id | anchor | target | context | |
|---|---|---|---|---|
| count | 36473 | 36473 | 36473 | 36473 |
| unique | 36473 | 733 | 29340 | 106 |
| top | 37d61fd2272659b1 | component composite coating | composition | H01 |
| freq | 1 | 152 | 24 | 2186 |
In the describe output, freq is the number of rows with the top value in a given column.
df.query('anchor == "component composite coating"').shape(152, 5)Structure the input data:
df['input'] = 'TEXT1: ' + df.context + '; TEXT2: ' + df.target + '; ANC1: ' + df.anchordf.input.head()0 TEXT1: A47; TEXT2: abatement of pollution; ANC...
1 TEXT1: A47; TEXT2: act of abating; ANC1: abate...
2 TEXT1: A47; TEXT2: active catalyst; ANC1: abat...
3 TEXT1: A47; TEXT2: eliminating process; ANC1: ...
4 TEXT1: A47; TEXT2: forest region; ANC1: abatement
Name: input, dtype: objectTokenization
Transformers use a Dataset object for storing a dataset. We can create one like so:
from datasets import Dataset, DatasetDict
ds = Dataset.from_pandas(df)dsDataset({
features: ['id', 'anchor', 'target', 'context', 'score', 'input'],
num_rows: 36473
})A deep learning model expects numbers as inputs, not English sentences! So we need to do two things:
- Tokenization: Split each text up into words (tokens).
- Numericalization: Convert each word (or token) into a number.
The details on how this is done depends on the model. So pick a model first:
model_nm = 'microsoft/deberta-v3-small'AutoTokenizer will create a tokenizer appropriate for a given model:
from transformers import AutoModelForSequenceClassification,AutoTokenizer
tokz = AutoTokenizer.from_pretrained(model_nm)Special tokens have been added in the vocabulary, make sure the associated word embeddings are fine-tuned or trained.
/usr/local/lib/python3.10/dist-packages/transformers/convert_slow_tokenizer.py:470: UserWarning: The sentencepiece tokenizer that you are converting to a fast tokenizer uses the byte fallback option which is not implemented in the fast tokenizers. In practice this means that the fast version of the tokenizer can produce unknown tokens whereas the sentencepiece version would have converted these unknown tokens into a sequence of byte tokens matching the original piece of text.
warnings.warn(
Special tokens have been added in the vocabulary, make sure the associated word embeddings are fine-tuned or trained.Here’s an example of how the tokenizer splits a text into “tokens” (which are like words, but can be sub-word pieces):
tokz.tokenize("G'day folks, I'm Jeremy from fast.ai!")['▁G',
"'",
'day',
'▁folks',
',',
'▁I',
"'",
'm',
'▁Jeremy',
'▁from',
'▁fast',
'.',
'ai',
'!']Uncommon words will be split into pieces. The start of a new word is represented by _.
tokz.tokenize("A platypus is an ornithorhynchus anatinus.")['▁A',
'▁platypus',
'▁is',
'▁an',
'▁or',
'ni',
'tho',
'rhynch',
'us',
'▁an',
'at',
'inus',
'.']Here’s a simple function which tokenizes our inputs:
def tok_func(x): return tokz(x["input"])To run this quickly in parallel on every row in our dataset, use map:
tok_ds = ds.map(tok_func, batched=True)This adds a new item to our dataset called input_ids. For instance, here is the input and IDs for the first row of our data:
row = tok_ds[0]
row['input'], row['input_ids']('TEXT1: A47; TEXT2: abatement of pollution; ANC1: abatement',
[1,
54453,
435,
294,
336,
5753,
346,
54453,
445,
294,
47284,
265,
6435,
346,
23702,
435,
294,
47284,
2])There’s a list called vocab in the tokenizer which contains a unique integer for every possible token string. We can look them up like this, for instance to find the token for the word “of”:
tokz.vocab['▁of']265265 is present in our input_ids for the first row of data.
tokz.vocab['of']1580Finally, we need to prepare our labels. Transformers always assumes that your labels has the column name labels, but in our dataset it’s currently score. Therefore, we need to rename it:
tok_ds = tok_ds.rename_columns({'score':'labels'})Test and validation sets
eval_df = pd.read_csv(path/'test.csv')
eval_df.describe()| id | anchor | target | context | |
|---|---|---|---|---|
| count | 36 | 36 | 36 | 36 |
| unique | 36 | 34 | 36 | 29 |
| top | 4112d61851461f60 | el display | inorganic photoconductor drum | G02 |
| freq | 1 | 2 | 1 | 3 |
This is the test set. Possibly the most important idea in machine learning is that of having separate training, validation, and test data sets.
Validation set
To explain the motivation, let’s start simple, and imagine we’re trying to fit a model where the true relationship is this quadratic:
def f(x): return -3*x**2 + 2*x + 20Unfortunately matplotlib (the most common library for plotting in Python) doesn’t come with a way to visualize a function, so we’ll write something to do this ourselves:
import numpy as np
import matplotlib.pyplot as plt
def plot_function(f, min=-2.1, max=2.1, color='r'):
x = np.linspace(min,max, 100)[:,None]
plt.plot(x, f(x), color)For instance, perhaps we’ve measured the height above ground of an object before and after some event. The measurements will have some random error. We can use numpy’s random number generator to simulate that. I like to use seed when writing about simulations like this so that I know you’ll see the same thing I do:
from numpy.random import normal,seed,uniform
np.random.seed(42)def noise(x, scale): return normal(scale=scale, size=x.shape)
def add_noise(x, mult, add): return x * (1+noise(x,mult)) + noise(x,add)Now let’s see what happens if we underfit or overfit these predictions. To do that, we’ll create a function that fits a polynomial of some degree (e.g. a line is degree 1, quadratic is degree 2, cubic is degree 3, etc). The details of how this function works don’t matter too much so feel free to skip over it if you like!
from sklearn.linear_model import LinearRegression
from sklearn.preprocessing import PolynomialFeatures
from sklearn.pipeline import make_pipeline
def plot_poly(degree):
model = make_pipeline(PolynomialFeatures(degree), LinearRegression())
model.fit(x, y)
plt.scatter(x,y)
plot_function(model.predict)As you see, the points on the red line (the line we fitted) aren’t very close at all. This is under-fit – there’s not enough detail in our function to match our data.
And what happens if we fit a degree 10 polynomial to our measurements?
Well now it fits our data better, but it doesn’t look like it’ll do a great job predicting points other than those we measured – especially those in earlier or later time periods. This is over-fit – there’s too much detail such that the model fits our points, but not the underlying process we really care about.
Let’s try a degree 2 polynomial (a quadratic), and compare it to our “true” function (in blue):
That’s not bad at all!
So, how do we recognise whether our models are under-fit, over-fit, or “just right”? We use a validation set. This is a set of data that we “hold out” from training – we don’t let our model see it at all. If you use the fastai library, it automatically creates a validation set for you if you don’t have one, and will always report metrics (measurements of the accuracy of a model) using the validation set.
The validation set is only ever used to see how we’re doing. It’s never used as inputs to training the model.
Transformers uses a DatasetDict for holding your training and validation sets. To create one that contains 25% of our data for the validation set, and 75% for the training set, use train_test_split:
dds = tok_ds.train_test_split(0.25, seed=42)
ddsDatasetDict({
train: Dataset({
features: ['id', 'anchor', 'target', 'context', 'labels', 'input', 'input_ids', 'token_type_ids', 'attention_mask'],
num_rows: 27354
})
test: Dataset({
features: ['id', 'anchor', 'target', 'context', 'labels', 'input', 'input_ids', 'token_type_ids', 'attention_mask'],
num_rows: 9119
})
})As you see above, the validation set here is called test and not validate, so be careful!
In practice, a random split like we’ve used here might not be a good idea – here’s what Dr Rachel Thomas has to say about it:
“One of the most likely culprits for this disconnect between results in development vs results in production is a poorly chosen validation set (or even worse, no validation set at all). Depending on the nature of your data, choosing a validation set can be the most important step. Although sklearn offers a train_test_split method, this method takes a random subset of the data, which is a poor choice for many real-world problems.”
Test set
So that’s the validation set explained, and created. What about the “test set” then – what’s that for?
The test set is yet another dataset that’s held out from training. But it’s held out from reporting metrics too! The accuracy of your model on the test set is only ever checked after you’ve completed your entire training process, including trying different models, training methods, data processing, etc.
You see, as you try all these different things, to see their impact on the metrics on the validation set, you might just accidentally find a few things that entirely coincidentally improve your validation set metrics, but aren’t really better in practice. Given enough time and experiments, you’ll find lots of these coincidental improvements. That means you’re actually over-fitting to your validation set!
That’s why we keep a test set held back. Kaggle’s public leaderboard is like a test set that you can check from time to time. But don’t check too often, or you’ll be even over-fitting to the test set!
Kaggle has a second test set, which is yet another held-out dataset that’s only used at the end of the competition to assess your predictions. That’s called the “private leaderboard”.
We’ll use eval as our name for the test set, to avoid confusion with the test dataset that was created above.
eval_df['input'] = 'TEXT1: ' + eval_df.context + '; TEXT2: ' + eval_df.target + '; ANC1: ' + eval_df.anchor
eval_ds = Dataset.from_pandas(eval_df).map(tok_func, batched=True)Metrics and correlation
When we’re training a model, there will be one or more metrics that we’re interested in maximising or minimising. These are the measurements that should, hopefully, represent how well our model will works for us.
In real life, outside of Kaggle, things not easy… As my partner Dr Rachel Thomas notes in The problem with metrics is a big problem for AI:
At their heart, what most current AI approaches do is to optimize metrics. The practice of optimizing metrics is not new nor unique to AI, yet AI can be particularly efficient (even too efficient!) at doing so. This is important to understand, because any risks of optimizing metrics are heightened by AI. While metrics can be useful in their proper place, there are harms when they are unthinkingly applied. Some of the scariest instances of algorithms run amok all result from over-emphasizing metrics. We have to understand this dynamic in order to understand the urgent risks we are facing due to misuse of AI.
In Kaggle, however, it’s very straightforward to know what metric to use: Kaggle will tell you! According to this competition’s evaluation page, “submissions are evaluated on the Pearson correlation coefficient between the predicted and actual similarity scores.” This coefficient is usually abbreviated using the single letter r. It is the most widely used measure of the degree of relationship between two variables.
r can vary between -1, which means perfect inverse correlation, and +1, which means perfect positive correlation. The mathematical formula for it is much less important than getting a good intuition for what the different values look like. To start to get that intuition, let’s look at some examples using the California Housing dataset, which shows “is the median house value for California districts, expressed in hundreds of thousands of dollars”. This dataset is provided by the excellent scikit-learn library, which is the most widely used library for machine learning outside of deep learning.
from sklearn.datasets import fetch_california_housing
housing = fetch_california_housing(as_frame=True)
housing = housing['data'].join(housing['target']).sample(1000, random_state=52)
housing.head()| MedInc | HouseAge | AveRooms | AveBedrms | Population | AveOccup | Latitude | Longitude | MedHouseVal | |
|---|---|---|---|---|---|---|---|---|---|
| 7506 | 3.0550 | 37.0 | 5.152778 | 1.048611 | 729.0 | 5.062500 | 33.92 | -118.28 | 1.054 |
| 4720 | 3.0862 | 35.0 | 4.697897 | 1.055449 | 1159.0 | 2.216061 | 34.05 | -118.37 | 3.453 |
| 12888 | 2.5556 | 24.0 | 4.864905 | 1.129222 | 1631.0 | 2.395007 | 38.66 | -121.35 | 1.057 |
| 13344 | 3.0057 | 32.0 | 4.212687 | 0.936567 | 1378.0 | 5.141791 | 34.05 | -117.64 | 0.969 |
| 7173 | 1.9083 | 42.0 | 3.888554 | 1.039157 | 1535.0 | 4.623494 | 34.05 | -118.19 | 1.192 |
We can see all the correlation coefficients for every combination of columns in this dataset by calling np.corrcoef:
np.set_printoptions(precision=2, suppress=True)
np.corrcoef(housing, rowvar=False)array([[ 1. , -0.12, 0.43, -0.08, 0.01, -0.07, -0.12, 0.04, 0.68],
[-0.12, 1. , -0.17, -0.06, -0.31, 0. , 0.03, -0.13, 0.12],
[ 0.43, -0.17, 1. , 0.76, -0.09, -0.07, 0.12, -0.03, 0.21],
[-0.08, -0.06, 0.76, 1. , -0.08, -0.07, 0.09, 0. , -0.04],
[ 0.01, -0.31, -0.09, -0.08, 1. , 0.16, -0.15, 0.13, 0. ],
[-0.07, 0. , -0.07, -0.07, 0.16, 1. , -0.16, 0.17, -0.27],
[-0.12, 0.03, 0.12, 0.09, -0.15, -0.16, 1. , -0.93, -0.16],
[ 0.04, -0.13, -0.03, 0. , 0.13, 0.17, -0.93, 1. , -0.03],
[ 0.68, 0.12, 0.21, -0.04, 0. , -0.27, -0.16, -0.03, 1. ]])This works well when we’re getting a bunch of values at once, but it’s overkill when we want a single coefficient:
np.corrcoef(housing.MedInc, housing.MedHouseVal)array([[1. , 0.68],
[0.68, 1. ]])Therefore, we’ll create this little function to just return the single number we need given a pair of variables:
def corr(x,y): return np.corrcoef(x,y)[0][1]
corr(housing.MedInc, housing.MedHouseVal)0.6760250732906Now we’ll look at a few examples of correlations, using this function (the details of the function don’t matter too much):
def show_corr(df, a, b):
x,y = df[a],df[b]
plt.scatter(x,y, alpha=0.5, s=4)
plt.title(f'{a} vs {b}; r: {corr(x, y):.2f}')So that’s what a correlation of 0.68 looks like. It’s quite a close relationship, but there’s still a lot of variation. (Incidentally, this also shows why looking at your data is so important – we can see clearly in this plot that house prices above $500,000 seem to have been truncated to that maximum value).
Let’s take a look at another pair:
The relationship looks like it is similarly close to the previous example, but r is much lower than the income vs valuation case. Why is that? The reason is that there are a lot of outliers – values of AveRooms well outside the mean.
r is very sensitive to outliers. If there’s outliers in your data, then the relationship between them will dominate the metric. In this case, the houses with a very high number of rooms don’t tend to be that valuable, so it’s decreasing r from where it would otherwise be.
Let’s remove the outliers and try again:
As we expected, now the correlation is very similar to our first comparison.
Here’s another relationship using AveRooms on the subset:
At this level, with r of 0.34, the relationship is becoming quite weak.
Let’s look at one more:
As you see here, a correlation of -0.2 shows a very weak negative trend.
We’ve seen now examples of a variety of levels of correlation coefficient, so hopefully you’re getting a good sense of what this metric means.
Transformers expects metrics to be returned as a dict, since that way the trainer knows what label to use, so let’s create a function to do that:
def corr_d(eval_pred): return {'pearson': corr(*eval_pred)}Training Our Model
To train a model in Transformers we’ll need this:
from transformers import TrainingArguments,TrainerWe pick a batch size that fits our GPU, and small number of epochs so we can run experiments quickly:
bs = 128
epochs = 4The most important hyperparameter is the learning rate. fastai provides a learning rate finder to help you figure this out, but Transformers doesn’t, so you’ll just have to use trial and error. The idea is to find the largest value you can, but which doesn’t result in training failing.
lr = 8e-5Transformers uses the TrainingArguments class to set up arguments. Don’t worry too much about the values we’re using here – they should generally work fine in most cases. It’s just the 3 parameters above that you may need to change for different models.
args = TrainingArguments('outputs', learning_rate=lr, warmup_ratio=0.1, lr_scheduler_type='cosine', fp16=True,
evaluation_strategy="epoch", per_device_train_batch_size=bs, per_device_eval_batch_size=bs*2,
num_train_epochs=epochs, weight_decay=0.01, report_to='none')We can now create our model, and Trainer, which is a class which combines the data and model together (just like Learner in fastai):
model = AutoModelForSequenceClassification.from_pretrained(model_nm, num_labels=1)
trainer = Trainer(model, args, train_dataset=dds['train'], eval_dataset=dds['test'],
tokenizer=tokz, compute_metrics=corr_d)Some weights of DebertaV2ForSequenceClassification were not initialized from the model checkpoint at microsoft/deberta-v3-small and are newly initialized: ['classifier.bias', 'classifier.weight', 'pooler.dense.weight', 'pooler.dense.bias']
You should probably TRAIN this model on a down-stream task to be able to use it for predictions and inference.Let’s train our model!
trainer.train();/usr/local/lib/python3.10/dist-packages/transformers/optimization.py:411: FutureWarning: This implementation of AdamW is deprecated and will be removed in a future version. Use the PyTorch implementation torch.optim.AdamW instead, or set `no_deprecation_warning=True` to disable this warning
warnings.warn(
You're using a DebertaV2TokenizerFast tokenizer. Please note that with a fast tokenizer, using the `__call__` method is faster than using a method to encode the text followed by a call to the `pad` method to get a padded encoding.| Epoch | Training Loss | Validation Loss | Pearson |
|---|---|---|---|
| 1 | No log | 0.032255 | 0.790911 |
| 2 | No log | 0.023222 | 0.814958 |
| 3 | 0.040500 | 0.022491 | 0.828246 |
| 4 | 0.040500 | 0.023501 | 0.828109 |
The key thing to look at is the “Pearson” value in table above. As you see, it’s increasing, and is already above 0.8. That’s great news! We can now submit our predictions to Kaggle if we want them to be scored on the official leaderboard. Let’s get some predictions on the test set:
preds = trainer.predict(eval_ds).predictions.astype(float)
predsarray([[ 0.58],
[ 0.69],
[ 0.57],
[ 0.33],
[-0.01],
[ 0.5 ],
[ 0.55],
[-0.01],
[ 0.31],
[ 1.15],
[ 0.29],
[ 0.24],
[ 0.76],
[ 0.91],
[ 0.75],
[ 0.43],
[ 0.33],
[-0.01],
[ 0.66],
[ 0.33],
[ 0.46],
[ 0.26],
[ 0.18],
[ 0.22],
[ 0.59],
[-0.04],
[-0.02],
[ 0.01],
[-0.03],
[ 0.59],
[ 0.3 ],
[-0. ],
[ 0.68],
[ 0.52],
[ 0.47],
[ 0.23]])Look out - some of our predictions are <0, or >1! This once again shows the value of remember to actually look at your data. Let’s fix those out-of-bounds predictions:
preds = np.clip(preds, 0, 1)predsarray([[0.58],
[0.69],
[0.57],
[0.33],
[0. ],
[0.5 ],
[0.55],
[0. ],
[0.31],
[1. ],
[0.29],
[0.24],
[0.76],
[0.91],
[0.75],
[0.43],
[0.33],
[0. ],
[0.66],
[0.33],
[0.46],
[0.26],
[0.18],
[0.22],
[0.59],
[0. ],
[0. ],
[0.01],
[0. ],
[0.59],
[0.3 ],
[0. ],
[0.68],
[0.52],
[0.47],
[0.23]])Notebook Exercise: Deeper Dive: Iterate like a grandmaster!
In this section I’ll run through the explanation and code provided in Jeremy’s notebook here.
In this notebook I’ll try to give a taste of how a competitions grandmaster might tackle the U.S. Patent Phrase to Phrase Matching competition. The focus generally should be two things:
- Creating an effective validation set
- Iterating rapidly to find changes which improve results on the validation set.
If you can do these two things, then you can try out lots of experiments and find what works, and what doesn’t. Without these two things, it will be nearly impossible to do well in a Kaggle competition (and, indeed, to create highly accurate models in real life!)
The more code you have, the more you have to maintain, and the more chances there are to make mistakes. So keep it simple!
from pathlib import Path
import os
iskaggle = os.environ.get('KAGGLE_KERNEL_RUN_TYPE', '')
if iskaggle:
!pip install -Uqq fastai
else:
import zipfile,kaggle
path = Path('us-patent-phrase-to-phrase-matching')
kaggle.api.competition_download_cli(str(path))
zipfile.ZipFile(f'{path}.zip').extractall(path)Downloading us-patent-phrase-to-phrase-matching.zip to /content100%|██████████| 682k/682k [00:00<00:00, 1.49MB/s]from fastai.imports import *if iskaggle: path = Path('../input/us-patent-phrase-to-phrase-matching')
path.ls()(#3) [Path('us-patent-phrase-to-phrase-matching/sample_submission.csv'),Path('us-patent-phrase-to-phrase-matching/test.csv'),Path('us-patent-phrase-to-phrase-matching/train.csv')]Let’s look at the training set:
df = pd.read_csv(path/'train.csv')
df| id | anchor | target | context | score | |
|---|---|---|---|---|---|
| 0 | 37d61fd2272659b1 | abatement | abatement of pollution | A47 | 0.50 |
| 1 | 7b9652b17b68b7a4 | abatement | act of abating | A47 | 0.75 |
| 2 | 36d72442aefd8232 | abatement | active catalyst | A47 | 0.25 |
| 3 | 5296b0c19e1ce60e | abatement | eliminating process | A47 | 0.50 |
| 4 | 54c1e3b9184cb5b6 | abatement | forest region | A47 | 0.00 |
| ... | ... | ... | ... | ... | ... |
| 36468 | 8e1386cbefd7f245 | wood article | wooden article | B44 | 1.00 |
| 36469 | 42d9e032d1cd3242 | wood article | wooden box | B44 | 0.50 |
| 36470 | 208654ccb9e14fa3 | wood article | wooden handle | B44 | 0.50 |
| 36471 | 756ec035e694722b | wood article | wooden material | B44 | 0.75 |
| 36472 | 8d135da0b55b8c88 | wood article | wooden substrate | B44 | 0.50 |
36473 rows × 5 columns
And the test set:
eval_df = pd.read_csv(path/'test.csv')
len(eval_df)36eval_df.head()| id | anchor | target | context | |
|---|---|---|---|---|
| 0 | 4112d61851461f60 | opc drum | inorganic photoconductor drum | G02 |
| 1 | 09e418c93a776564 | adjust gas flow | altering gas flow | F23 |
| 2 | 36baf228038e314b | lower trunnion | lower locating | B60 |
| 3 | 1f37ead645e7f0c8 | cap component | upper portion | D06 |
| 4 | 71a5b6ad068d531f | neural stimulation | artificial neural network | H04 |
df.target.value_counts()composition 24
data 22
metal 22
motor 22
assembly 21
..
switching switch over valve 1
switching switch off valve 1
switching over valve 1
switching off valve 1
wooden substrate 1
Name: target, Length: 29340, dtype: int64We see that there’s nearly as many unique targets as items in the training set, so they’re nearly but not quite unique. Most importantly, we can see that these generally contain very few words (1-4 words in the above sample).
df.anchor.value_counts()component composite coating 152
sheet supply roller 150
source voltage 140
perfluoroalkyl group 136
el display 135
...
plug nozzle 2
shannon 2
dry coating composition1 2
peripheral nervous system stimulation 1
conduct conducting material 1
Name: anchor, Length: 733, dtype: int64We can see here that there’s far fewer unique values (just 733) and that again they’re very short (2-4 words in this sample).
df.context.value_counts()H01 2186
H04 2177
G01 1812
A61 1477
F16 1091
...
B03 47
F17 33
B31 24
A62 23
F26 18
Name: context, Length: 106, dtype: int64The first character is the section the patent was filed under – let’s create a column for that and look at the distribution:
df['section'] = df.context.str[0]
df.section.value_counts()B 8019
H 6195
G 6013
C 5288
A 4094
F 4054
E 1531
D 1279
Name: section, dtype: int64Finally, we’ll take a look at a histogram of the scores:
There’s a small number that are scored 1.0 - here’s a sample:
df[df.score==1]| id | anchor | target | context | score | section | |
|---|---|---|---|---|---|---|
| 28 | 473137168ebf7484 | abatement | abating | F24 | 1.0 | F |
| 158 | 621b048d70aa8867 | absorbent properties | absorbent characteristics | D01 | 1.0 | D |
| 161 | bc20a1c961cb073a | absorbent properties | absorption properties | D01 | 1.0 | D |
| 311 | e955700dffd68624 | acid absorption | absorption of acid | B08 | 1.0 | B |
| 315 | 3a09aba546aac675 | acid absorption | acid absorption | B08 | 1.0 | B |
| ... | ... | ... | ... | ... | ... | ... |
| 36398 | 913141526432f1d6 | wiring trough | wiring troughs | F16 | 1.0 | F |
| 36435 | ee0746f2a8ecef97 | wood article | wood articles | B05 | 1.0 | B |
| 36440 | ecaf479135cf0dfd | wood article | wooden article | B05 | 1.0 | B |
| 36464 | 8ceaa2b5c2d56250 | wood article | wood article | B44 | 1.0 | B |
| 36468 | 8e1386cbefd7f245 | wood article | wooden article | B44 | 1.0 | B |
1154 rows × 6 columns
We can see from this that these are just minor rewordings of the same concept, and isn’t likely to be specific to context. Any pretrained model should be pretty good at finding these already.
Training
! pip install transformers[sentencepiece] datasets acceleratefrom torch.utils.data import DataLoader
import warnings,transformers,logging,torch
from transformers import TrainingArguments,Trainer
from transformers import AutoModelForSequenceClassification,AutoTokenizerif iskaggle:
!pip install -q datasets
import datasets
from datasets import load_dataset, Dataset, DatasetDict# quiet huggingface warnings
warnings.simplefilter('ignore')
logging.disable(logging.WARNING)# specify which model we are going to be using
model_nm = 'microsoft/deberta-v3-small'We can now create a tokenizer for this model. Note that pretrained models assume that text is tokenized in a particular way. In order to ensure that your tokenizer matches your model, use the AutoTokenizer, passing in your model name.
tokz = AutoTokenizer.from_pretrained(model_nm)We’ll need to combine the context, anchor, and target together somehow. There’s not much research as to the best way to do this, so we may need to iterate a bit. To start with, we’ll just combine them all into a single string. The model will need to know where each section starts, so we can use the special separator token to tell it:
sep = tokz.sep_token
sep'[SEP]'df['inputs'] = df.context + sep + df.anchor + sep + df.targetGenerally we’ll get best performance if we convert pandas DataFrames into HuggingFace Datasets, so we’ll convert them over, and also rename the score column to what Transformers expects for the dependent variable, which is label:
ds = Dataset.from_pandas(df).rename_column('score', 'label')
eval_ds = Dataset.from_pandas(eval_df)To tokenize the data, we’ll create a function (since that’s what Dataset.map will need):
def tok_func(x): return tokz(x["inputs"])tok_func(ds[0]){'input_ids': [1, 336, 5753, 2, 47284, 2, 47284, 265, 6435, 2], 'token_type_ids': [0, 0, 0, 0, 0, 0, 0, 0, 0, 0], 'attention_mask': [1, 1, 1, 1, 1, 1, 1, 1, 1, 1]}The only bit we care about at the moment is input_ids. We can see in the tokens that it starts with a special token 1 (which represents the start of text), and then has our three fields separated by the separator token 2. We can check the indices of the special token IDs like so:
tokz.all_special_tokens['[CLS]', '[SEP]', '[UNK]', '[PAD]', '[MASK]']We can now tokenize the input. We’ll use batching to speed it up, and remove the columns we no longer need:
inps = "anchor","target","context"
tok_ds = ds.map(tok_func, batched=True, remove_columns=inps+('inputs','id','section'))Looking at the first item of the dataset we should see the same information as when we checked tok_func above:
tok_ds[0]{'label': 0.5,
'input_ids': [1, 336, 5753, 2, 47284, 2, 47284, 265, 6435, 2],
'token_type_ids': [0, 0, 0, 0, 0, 0, 0, 0, 0, 0],
'attention_mask': [1, 1, 1, 1, 1, 1, 1, 1, 1, 1]}Creating a validation set
According to this post, the private test anchors do not overlap with the training set. So let’s do the same thing for our validation set.
First, create a randomly shuffled list of anchors:
anchors = df.anchor.unique()
np.random.seed(42)
np.random.shuffle(anchors)
anchors[:5]array(['time digital signal', 'antiatherosclerotic', 'filled interior',
'dispersed powder', 'locking formation'], dtype=object)Now we can pick some proportion (e.g 25%) of these anchors to go in the validation set:
val_prop = 0.25
val_sz = int(len(anchors)*val_prop)
val_anchors = anchors[:val_sz]Now we can get a list of which rows match val_anchors, and get their indices:
# is_val is a boolean array
is_val = np.isin(df.anchor, val_anchors)
idxs = np.arange(len(df))
val_idxs = idxs[ is_val]
trn_idxs = idxs[~is_val]
len(val_idxs),len(trn_idxs)(9116, 27357)Our training and validation Datasets can now be selected, and put into a DatasetDict ready for training:
dds = DatasetDict({"train":tok_ds.select(trn_idxs),
"test": tok_ds.select(val_idxs)})BTW, a lot of people do more complex stuff for creating their validation set, but with a dataset this large there’s not much point. As you can see, the mean scores in the two groups are very similar despite just doing a random shuffle:
df.iloc[trn_idxs].score.mean(),df.iloc[val_idxs].score.mean()(0.3623021530138539, 0.3613426941641071)Initial model
Let’s now train our model! We’ll need to specify a metric, which is the correlation coefficient provided by numpy (we need to return a dictionary since that’s how Transformers knows what label to use):
def corr(eval_pred): return {'pearson': np.corrcoef(*eval_pred)[0][1]}We pick a learning rate and batch size that fits our GPU, and pick a reasonable weight decay and small number of epochs:
lr,bs = 8e-5,128
wd,epochs = 0.01,4Transformers uses the TrainingArguments class to set up arguments. We’ll use a cosine scheduler with warmup, since at fast.ai we’ve found that’s pretty reliable. We’ll use fp16 since it’s much faster on modern GPUs, and saves some memory. We evaluate using double-sized batches, since no gradients are stored so we can do twice as many rows at a time.
def get_trainer(dds):
args = TrainingArguments('outputs', learning_rate=lr, warmup_ratio=0.1, lr_scheduler_type='cosine', fp16=True,
evaluation_strategy="epoch", per_device_train_batch_size=bs, per_device_eval_batch_size=bs*2,
num_train_epochs=epochs, weight_decay=wd, report_to='none')
model = AutoModelForSequenceClassification.from_pretrained(model_nm, num_labels=1)
return Trainer(model, args, train_dataset=dds['train'], eval_dataset=dds['test'],
tokenizer=tokz, compute_metrics=corr)args = TrainingArguments('outputs', learning_rate=lr, warmup_ratio=0.1, lr_scheduler_type='cosine', fp16=True,
evaluation_strategy="epoch", per_device_train_batch_size=bs, per_device_eval_batch_size=bs*2,
num_train_epochs=epochs, weight_decay=wd, report_to='none')We can now create our model, and Trainer, which is a class which combines the data and model together (just like Learner in fastai):
model = AutoModelForSequenceClassification.from_pretrained(model_nm, num_labels=1)
trainer = Trainer(model, args, train_dataset=dds['train'], eval_dataset=dds['test'],
tokenizer=tokz, compute_metrics=corr)trainer.train();| Epoch | Training Loss | Validation Loss | Pearson |
|---|---|---|---|
| 1 | No log | 0.027171 | 0.794542 |
| 2 | No log | 0.026872 | 0.811033 |
| 3 | 0.035300 | 0.024633 | 0.816882 |
| 4 | 0.035300 | 0.024581 | 0.817413 |
Improving the model
We now want to start iterating to improve this. To do that, we need to know whether the model gives stable results. I tried training it 3 times from scratch, and got a range of outcomes from 0.808-0.810. This is stable enough to make a start - if we’re not finding improvements that are visible within this range, then they’re not very significant! Later on, if and when we feel confident that we’ve got the basics right, we can use cross validation and more epochs of training.
Iteration speed is critical, so we need to quickly be able to try different data processing and trainer parameters. So let’s create a function to quickly apply tokenization and create our DatasetDict:
def get_dds(df):
ds = Dataset.from_pandas(df).rename_column('score', 'label')
tok_ds = ds.map(tok_func, batched=True, remove_columns=inps+('inputs','id','section'))
return DatasetDict({"train":tok_ds.select(trn_idxs), "test": tok_ds.select(val_idxs)})def get_model(): return AutoModelForSequenceClassification.from_pretrained(model_nm, num_labels=1)def get_trainer(dds, model=None):
if model is None: model = get_model()
args = TrainingArguments('outputs', learning_rate=lr, warmup_ratio=0.1, lr_scheduler_type='cosine', fp16=True,
evaluation_strategy="epoch", per_device_train_batch_size=bs, per_device_eval_batch_size=bs*2,
num_train_epochs=epochs, weight_decay=wd, report_to='none')
return Trainer(model, args, train_dataset=dds['train'], eval_dataset=dds['test'],
tokenizer=tokz, compute_metrics=corr)Perhaps using the special separator character isn’t a good idea, and we should use something we create instead. Let’s see if that makes things better. First we’ll change the separator and create the DatasetDict:
sep = " [s] "
df['inputs'] = df.context + sep + df.anchor + sep + df.target
dds = get_dds(df)get_trainer(dds).train()| Epoch | Training Loss | Validation Loss | Pearson |
|---|---|---|---|
| 1 | No log | 0.027216 | 0.799765 |
| 2 | No log | 0.025568 | 0.814325 |
| 3 | 0.031000 | 0.023474 | 0.817759 |
| 4 | 0.031000 | 0.024206 | 0.817377 |
TrainOutput(global_step=856, training_loss=0.023552694610346144, metrics={'train_runtime': 207.9058, 'train_samples_per_second': 526.335, 'train_steps_per_second': 4.117, 'total_flos': 582121520370810.0, 'train_loss': 0.023552694610346144, 'epoch': 4.0})That’s looking quite a bit better, so we’ll keep that change.
(Vishal note: I trained it a few times but couldn’t get the pearson coefficient past 0.8174)
Often changing to lowercase is helpful. Let’s see if that helps too:
df['inputs'] = df.inputs.str.lower()
dds = get_dds(df)
get_trainer(dds).train()| Epoch | Training Loss | Validation Loss | Pearson |
|---|---|---|---|
| 1 | No log | 0.025207 | 0.798847 |
| 2 | No log | 0.024926 | 0.813183 |
| 3 | 0.031800 | 0.023556 | 0.815640 |
| Epoch | Training Loss | Validation Loss | Pearson |
|---|---|---|---|
| 1 | No log | 0.025207 | 0.798847 |
| 2 | No log | 0.024926 | 0.813183 |
| 3 | 0.031800 | 0.023556 | 0.815640 |
| 4 | 0.031800 | 0.024359 | 0.815295 |
TrainOutput(global_step=856, training_loss=0.024133934595874536, metrics={'train_runtime': 197.3858, 'train_samples_per_second': 554.386, 'train_steps_per_second': 4.337, 'total_flos': 582121520370810.0, 'train_loss': 0.024133934595874536, 'epoch': 4.0})Special tokens
What if we made the patent section a special token? Then potentially the model might learn to recognize that different sections need to be handled in different ways. To do that, we’ll use, e.g. [A] for section A. We’ll then add those as special tokens:
df['sectok'] = '[' + df.section + ']'
sectoks = list(df.sectok.unique())
tokz.add_special_tokens({'additional_special_tokens': sectoks})8df['inputs'] = df.sectok + sep + df.context + sep + df.anchor.str.lower() + sep + df.target
dds = get_dds(df)Since we’ve added more tokens, we need to resize the embedding matrix in the model:
model = get_model()
model.resize_token_embeddings(len(tokz))Embedding(128009, 768)trainer = get_trainer(dds, model=model)
trainer.train()| Epoch | Training Loss | Validation Loss | Pearson |
|---|---|---|---|
| 1 | No log | 0.025942 | 0.810038 |
| 2 | No log | 0.025694 | 0.814332 |
| 3 | 0.010500 | 0.023547 | 0.816508 |
| 4 | 0.010500 | 0.024562 | 0.817200 |
TrainOutput(global_step=856, training_loss=0.009868621826171875, metrics={'train_runtime': 221.7169, 'train_samples_per_second': 493.548, 'train_steps_per_second': 3.861, 'total_flos': 695370741753690.0, 'train_loss': 0.009868621826171875, 'epoch': 4.0})Before submitting a model, retrain it on the full dataset, rather than just the 75% training subset we’ve used here. Create a function like the ones above to make that easy for you!
Video Notes
In this section, I’ll take notes while watching this lesson’s video.
- Introduction
- In the book, we do NLP using Recurrent Neural Networks (RNNs).
- In the video, we’re going to be fine-tuning a pretrained NLP model using a library called HuggingFace Transformers.
- It’s useful to have experience in using more than one library. See the same concepts applied in different ways. Great for understanding the concepts.
- HuggingFace libraries are SOTA in NLP.
- Transformers library in process of being integrated into fastai library.
- HuggingFace Transformers doesn’t have the same layered API as fastai.
- Fine-Tuning a Pretrained Model
- In the quadratic/sliders example, a pretrained model is like someone telling you that they are confident what parameter
ashould be, are somewhat confident whatbshould be, and have no idea whatcshould be. Then, we would traincuntil it firts our model, adjustband keepaas is. That’s what it’s like fine-tuning a pretrained model. - A pretrained model is a bunch of parameters have already been fit, where for some of them we’re pretty confident of what they should be, and for some of them we really have no idea at all.
- Fine-tuning is the process of taking those ones where we have no idea at all what they should be and trying to get them right, and then moving the other ones a little bit.
- In the quadratic/sliders example, a pretrained model is like someone telling you that they are confident what parameter
- ULMFiT
- The idea of fine-tuning a pretrained NLP model was pioneered by ULMFiT which was first introduced in a fastai course, later turned into an academic paper by Jeremy and Sebastian Ruder which inspired a huge change in NLP capabilities around the world.
- Step 1
- Build a language model using all of Wikipedia that tried to predict the next word of a Wikipedia article. Filling in these kinds of things requires understanding a lot about how language is structured and about the world. Getting good at fitting a language model requires a neural net getting good at a lot of things. It needs to understand language at a reasonably good level, what is true, what is not true, different ways in which things are expressed and so on. Started with random weights. At the end was a model that could predict more than 30% of the time correctly what the next word in a Wikipedia article would be.
- Step 2
- Create a second language model, that predicts the next word of a sentence. Took the pretrained model and ran a few more epochs using IMDb movie reviews. So it got very good at predicting the next work of an IMDb movie review.
- Step 3
- Took those weights and fine-tuned them for the task of predicting whether or not a movie review was positive or negative sentiment.
- The first two models don’t require labels. The labels was what’s the next word of the sentence.
- ULMFiT built with RNNs.
- Transformers developed at the same time of ULMFiT’s release.
- Transformers can take advantage of modern accelerators like Google’s TPUs.
- Transformers don’t allow you to predict the next word of a sentence, it’s just not how they are structured. Instead they deleted at random a few words and asked the model to predict what words were deleted. The basic concept similar to ULMFiT ,replaced RNN with Transformer. Replaced language model with masked language model.
- How do you go from a model that’s trained to predict the next word to a model that does classification?
- The first layer of ImageNet classification model finds basic features like diagonal edges, gradients, etc. Layer two combined those (ReLUs added together, activations from sets of ReLUs matrix multipled, etc.)
- Layer 5 had bird and lizard eyeball detectors, dog face detectors, flowers detectors, etc.
- Later layers do things much more specific to the training task.
- Pretty unlikely that you need to change the early layers.
- The layer that says “what is this” is deleted in fine-tuning (the layer that has one output per category). The model is then spitting out a few hundred activations. We stick a new random matrix on top of that and train it, so it can predict what you’re trying to predict. Then we gradually train the rest of the layers.
- Getting started with NLP for absolute beginners
- US Patent Phrase to Phrase Matching Competition.
- Classification is probably the most widely use case for NLP.
- Document = an input to an NLP model that contains text.
- Classifying a document is a rich thing to do: sentiment analysis, author identifiation, legal discovery, organizing documents by topic, triaging inbound emails.
- The Kaggle competition on US Patents does not immediately look like a classification problem.
- Columns: Anchor, target, context, score
- Goal: come up with a model that automatically determines which anchor and target pairs are talking about the same thing. score = 1.0 means the anchor and target mean the same thing, 0.0 means they are not.
- Whether the anchor and target are determined to be similar or not depends on the context.
- Represent the problem as
<constant string><anchor><seperator><constant string><target>and choose category 0.0, 0.25, 0.50, 0.75 or 1.00. - Kaggle data is already on Kaggle.
- Always look through the competition’s Data page and read through it before jumping into the data.
- Use
DataFrame.describe(include='object')to see stats about the fields (count, unique, top, frequency of top). - This dataset contains very small documents (3-4 words) that are not very unique. There’s not a lot of unique data to work with.
- Create a single string of anchor, target, and context with separators and store as the
inputcolumn. - Neural networks work with numbers: We’re going to take the numbers, multiply by matrices, replace negatives with zeros, add them up, and do this a few times.
- Tokenization: Split each document into tokens (words).
- The list of unique words is called the vocabulary.
- Numericalization: Each word in the vocabulrary gets a number. The bigger the vocab, the more memory gets used, the more data we need to train. We don’t want a large vocabulary.
- Tokenize into sub-words (pieces of words).
- We can turn a pandas DataFrame into a Huggingface dataset’s Dataset using
Dataset.from_pandas. - Whatever pretrained model you used comes with a tokenizer. Before you start tokenizing, you have to decide on which model to use.
- Hugginface Model Hub has pretrained models trained on specific corpuses.
- There are some generally good models,
deberta-v3is one of those. - NLP has been practically effective for general users for only a year or two, a lot of this stuff we’re figuring out as a community.
- Always start with a
smallmodel, it’s faster to train, we’re going to be able to do more iterations. AutoTokenizer.from_pretrained(<model name>)will download the vocab and details about how this particular model tokenized the dataset._represents the start of a word.def tok_func(x): return tokx(x['input'])takes a documentx, and tokenizes it’sinput.Dataset.mapwill parallelize the process of calling the function on each value.batched=Truewill do a bunch at a time. Tokenizer library is an optimized Rust library.input_idswill contain numbers in the position of each of the tokens.- How do you choose the keywords and the order of the fields when creating
input?- It’s arbitrary, try a few things. We just want something it can learn from that separates one field from another.
- If one of the fields was long (1000 characters) is there any special handling required there?
- Long documents in ULMFiT require no special consideration. ULMFiT is the best approach for large documents. It will split large documents into pieces.
- Large documents are challening for Transformers. It does the whole document at once.
- Documents over 2000 words: look at ULMFiT.
- Under 2000 words: Transformers should be fine unless you have a laptop GPU with not much memory.
- HuggingFace transformers expect that your target is a column called
labels. test.csvdoesn’t have ascorefield.- Perhaps the most important idea in machine learning is having separate training, validation and test datasets.
- Test and validation sets are all about identifying and controlling for overfitting.
- Underfit: not enough complexity in the model fit to match the data that’s there. It’s systematically biased.
- Common misunderstanding is that simpler models are more reliable in some way, but models that are too simple will be systematically incorrect.
- Overfit: it’s done a good job of fitting our data points, but if we sample some more data points from our distribution the model won’t be close to them.
- Underfitting is easy to recognize (we can look at training data and see that it’s not very close).
- Overfitting is harder to recognize because the training data is very close.
- How do we tell if we have a good fit that’s not overfitting? We measure how good our model is by looking ONLY at the points we set aside as the validation set.
- fast.ai won’t let you train a model without a validation set and shows metrics only on the validation set.
- Creating a good validation set is not generally as simple as just randomly pulling some of your data out of the data that you train your model on.
- Kaggle is a great place to learn how to create a good validation set.
- A test set is another validation set that you don’t use for metrics. Helps you see if you overfit using the validation set.
- Kaggle has two test sets: leaderboard feedback during competition and second test set that is private until after competition is finished.
- Don’t accidentally find a model that is good by coincidence. Only if you have a test set that you hold out will you know if you’ve done this.
- If your model is terrible on the test set—go back to square one.
- You don’t want functions with gradient of 0 of inf (like accuracy) you want something smooth.
- One metric is not enough to capture all of the real world dynamics involved in a model’s use.
- Goodhart’s law: when a measure becomes a target, it’s ceases to be a good measure.
- AI is really good at optimizing metrics so you have to be careful what metrics you choose for models that are used in real life (impacting people’s lives).
- Pearson correlation coefficient is the most widely used measure of how similar two variables are
- -1.0 to +1.0.
- Abbreviated as r.
- How do I plot datasets with far too many points? The answer is: get less points (sample).
np.corrcoefgives a diagonally symmetric matrix of r values.- Visualizing your data is important so you can see things like how data is truncated.
alpha=0.5for scatter plots creates darker areas where there’s lots of dots.- r relies on the square of the difference, big outliers increase that by a lot.
- r is very sensitive to outliers.
- If you’re trying to win a Kaggle competition that uses r and even a couple of your rows are really wrong, it will be a disaster.
- You almost can’t see the relationship for \(r=0.34\)
- Transformers expects metric to be returned as a
dict. tok_ds.train_test_split()returns aDatasetDict({train: Dataset, test: Dataset}).- Transformers calls it validation set
test, on which is calculates metrics. - The fastai equivalent of
Learneris the HuggingFace Transformer’sTrainer. - The larger the batch size, the more you can do in parallel and the faster it’ll be, but if it’s too large you’ll get an out-of-memory error on the GPU.
- If you’re using a framework that doesn’t have a learning rate finder like fastai, you can just start with a really low learning rate and then keep doubling it until it falls apart.
TrainingArgumentsis a class that takes all of the configuration (like learning rate, warmup ratio, scheduler type, weight decay, etc.).- You always want
fp16=Trueas it will be faster. AutoModelForSequenceClassificationwill create an model for classification,.from_pretrainedwill use a pretrained model which has anum_labelsparam which is the number of output columns we have, which in this case is 1 (the score).Trainertakes the model, the training and validation data,TrainingArguments(), tokenizer and metrics).Trainer.train()will train the model.- HuggingFace is very verbose, the warnings which you can ignore.
- The only reason we get a high r value after 4 epochs is because we used a pretrained model.
- The pretrained model already knows a lot about language and has a good sense of whether two phrases have the same meaning or not.
- How do you decide when it’s okay to remove outliers?
- Outliers should never just be removed for modelling.
- Instead we would observe that clearly from looking at this dataset, these two groups can’t be treated the same way (low income/high # of rooms vs. high income/high # of rooms). Split them into two separate analyses.
- Outlier exists in a statistical sense, it doesn’t exist in a real sense (i.e. things that we should ignore or throw away). Some of the most useful insights in data projects are digging into outliers and understanding what are they? and where did they come from? It’s in those edge cases where you discover really important things like when processes go wrong, labelling problems. Never delete outliers. Investigate them, have a strategy about what you’re going to do with them.
- Training with HuggingFace’s Transformer is similar to the things we’ve seen before with fastai.
trainer.predict(eval_ds).predictions.astype(float)to get predictions fromTrainerobject.- Always look at your outputs. So you can see things like having negative predictions or predictions over 1, which are outside the range of the patent phrase matching score. For now, we can at least round these off up to 0 and down to 1, respectively, better ways to do this but this is better than nothing.
- Kaggle expects submissions to generally be in a CSV file.
- NLP is probably where the biggest opportunities are for big wins in research and commercialization.
- It’s worth thinking about both use and misuse of modern NLP.
- You can create bots to generate context appropriate conversation and scale it up to 99% of Twitter and nobody would know. This is worrying because a lot of how people see the world is coming out of social media conversation, which at this point are contrallable. It would not be that hard to create something that’s optimized towards moving a point of view amongst a billion people in a very subtle way, very gradually over a long period of time by multiple bots each pretending to argue with each other and one of them getting the upper hand and so forth.
- What GPT is used for we may not know for decades, if ever.
- 2017: millions of submissions to the FTC about Net Neutrality very heavily biased against it. An analysis showed that something like 99% of them were auto-generated. We don’t know for sure but this seems successful because repealing Net Neutrality went through, the comments were factored into this decision.
- You can always create a generative model that beats bot classifiers designed to classify its content as auto-generated. Similar problem with spam prevention.
- If you pass
num_labels=1toAutoModelForSequenceClassificationit treats it as a regression problem.
Book Notes
In this section, I’ll take notes and run code examples from Chapter 10: NLP Deep Dive: RNNs in the textbook.
- In general, in NLP the pretrained model is trained on a different task.
- language model: a model that has been trained to guess the next word in a text (having read the ones before).
- self-supervised learning: Training a model using labels that are embedded in the independent variable, rather than requiring external labels.
- To properly guess the next word in a sentence, the model will have to develop an understanding of the natural language.
- Self-supervised learning is not usually used for the model that is trained directly, but instead is used for pretraining a model used for transfer learning.
- Self-supervised learning and computer vision
- Even if our language model knows the basics of the language we are using in the task (e.g., our pretrained model is in English), it helps to get used to the style of the corpus we are targeting.
- You get even better results if you fine-tune the sequence-based language model prior to fine-tuning the classification model.
- The IMDb dataset contains 100k movie reviews (50k unlabeled, 25k labeled training set reviews, 25k labeled validation set reviews). We can use all of these reviews to fine-tune the pretrained language model, which was trained only on Wikipedia articles, this will result in a language model that is particularly good at predicting the next word of a movie review. This is known as Universal Language Model Fine-tuning (ULMFiT).
- The extra stage of fine-tuning the language model, prior to transfer learning to classification task, resulted in significantly better predictions.
Text Preprocessing
- Using categorical variables as independent variables for a neural network:
- Make a list of all possible levels of that categorical variable (the vocab).
- Replace each level with its index in the vocab.
- Create an embedding matrix for this containing a row for each level (i.e., for each item of the vocab).
- Use this embedding matrix as the first layer of a neural network. (A dedicated embedding matrix can take as inputs the raw vocab indexes created in step 2; this is equivalent to, but faster and more efficient than, a matrix that takes as input one-hot-encoded vectors representing the indexes).
- We can do nearly the same thing with text:
- First we concatenate all of the documents in our dataset into one big long string and split it into words (or tokens), giving us a very long list of words.
- Our independent variable will be the sequence of words starting with the first word in our very long list and ending with the second to last, and our dependent variable will be the sequence of words starting with the second word and ending with the last word.
- Our vocab will consist of a mix of common words that are already in the vocabulary of our pretrained model and new words specific to our corpus.
- Our embedding matrix will be built accordingly: for words that are in the vocabulary of our pretrained model, we will take the corresponding row in the embedding matrix of the pretrained model; but for new words, we won’t have anything, so we will just initialize the corresponding row with a random vector.
- Steps for creating a language model:
- Tokenization: convert the text into a list of words (or characters, or substrings, depending on the granularity of your model)
- Numericalization: List all of the unique words that appear (vocab) and convert each word into a number by looking up its index in the vocab.
- Language model data loader creation: fastai’s
LMDataLoaderautomatically handles creating a dependent variable that is offset from the independent variable by one token, and handles important details liks shuffling the training data so that the dependent and independent variables maintain their structure as required. - Language model creation: we need a model that handles input lists that could be arbitrarily big or small. We use a Recurrent Neural Network (RNN).
Tokenization
There is no one approach to tokenization. There are three main approaches:
- Word-based: Split a sentence on spaces and separate parts of meaning even when there are no spaces (“don’t” -> “do n’t”). Punctuation marks are generally split into separate tokens.
- Subword based: Split words into smaller parts, based on the most commonly occurring substrings (“occasion” -> “o c ca sion”).
- Character-based: Split a sentence into its individual characters.
Word Tokenization with fastai
Rather than providing its own tokenizers, fastai provides a consistent interface to a range of tokenizers in external libraries.
Let’s try it out with the IMDb dataset:
from fastai.text.all import *
path = untar_data(URLs.IMDB)path.ls()(#7) [Path('/root/.fastai/data/imdb/unsup'),Path('/root/.fastai/data/imdb/tmp_lm'),Path('/root/.fastai/data/imdb/imdb.vocab'),Path('/root/.fastai/data/imdb/test'),Path('/root/.fastai/data/imdb/tmp_clas'),Path('/root/.fastai/data/imdb/train'),Path('/root/.fastai/data/imdb/README')]get_text_files gets all the text files in a path
files = get_text_files(path, folders = ['train', 'test', 'unsup'])files[:10](#10) [Path('/root/.fastai/data/imdb/unsup/42765_0.txt'),Path('/root/.fastai/data/imdb/unsup/19120_0.txt'),Path('/root/.fastai/data/imdb/unsup/8649_0.txt'),Path('/root/.fastai/data/imdb/unsup/32022_0.txt'),Path('/root/.fastai/data/imdb/unsup/30143_0.txt'),Path('/root/.fastai/data/imdb/unsup/14876_0.txt'),Path('/root/.fastai/data/imdb/unsup/28162_0.txt'),Path('/root/.fastai/data/imdb/unsup/32133_0.txt'),Path('/root/.fastai/data/imdb/unsup/21844_0.txt'),Path('/root/.fastai/data/imdb/unsup/830_0.txt')]Here’s a review that we will tokenize:
txt = files[0].open().read(); txt[:75]"Despite some humorous banter and a decent supporting cast, I can't really r"WordTokenizer will always point to fastai’s current default word tokenizer.
fastai’s coll_repr(collection, n) displays the first n items of collection, along with the full size.
tokz = WordTokenizer()
toks = first(tokz([txt]))
print(coll_repr(toks, 30))(#243) ['Despite','some','humorous','banter','and','a','decent','supporting','cast',',','I','ca',"n't",'really','recommend','this','movie','.','The','leads','are',"n't",'very','likable','and','I','did',"n't",'particularly','care'...]Tokenization is a surprisingly subtle task. “.” is separated when it terminates a sentence but not in an acronym or number:
first(tokz(['The U.S. dollar $1 is $1.00.']))(#9) ['The','U.S.','dollar','$','1','is','$','1.00','.']fastai adds some functionality to the tokenization process with the Tokenizer class:
tkn = Tokenizer(tokz)
print(coll_repr(tkn(txt), 31))(#264) ['xxbos','xxmaj','despite','some','humorous','banter','and','a','decent','supporting','cast',',','i','ca',"n't",'really','recommend','this','movie','.','xxmaj','the','leads','are',"n't",'very','likable','and','i','did',"n't"...]Tokens that start with xx are special tokens.
xxbos is a special token that indicates the start of a new text (“BOS” is a standard NLP acronym that means “beginning of stream”). By recognizing this start token, the model will be able to learn it needs to “forget” what was said previously and focus on upcoming words. These special tokens don’t come from the external tokenizer. fastai adds them by default by applying a number of rules when processing text. These rules are designed to make it easier for a model to recognize the important parts of a sentence. We are translating the original English language sequence into a simplified tokenized language that is designed to be easy for a model to learn.
For example, the rules will replace a sequence of four exclamation points with a single exclamation point follow by a special repeated character token and then the number four.
tkn('!!!!')(#4) ['xxbos','xxrep','4','!']In this way, the model’s embedding matrix can encode information about general concepts such as repeated punctuation rather than requiring a separate token for every number of repititions of every punctuation mark. A capitalized word will be replaced with a special capitalization token, followed by the lowercase version of the word so the embedding matrix needs only the lowercase version of the words saving compute and memory resources but can still learn the concept of capitalization.
Here are some of the main special tokens:
xxbos: Indicates the beginning of a text (in this case, a review).
xxmaj: Indicates the next word begins with a capital.
xxunk: Indicates the next word is unknown.
defaults.text_proc_rules[<function fastai.text.core.fix_html(x)>,
<function fastai.text.core.replace_rep(t)>,
<function fastai.text.core.replace_wrep(t)>,
<function fastai.text.core.spec_add_spaces(t)>,
<function fastai.text.core.rm_useless_spaces(t)>,
<function fastai.text.core.replace_all_caps(t)>,
<function fastai.text.core.replace_maj(t)>,
<function fastai.text.core.lowercase(t, add_bos=True, add_eos=False)>]fix_html: replaces special HTML characters with a readable version.
replace_rep: Replaces any character repeated three times or more with a special token for repetition (xxrep), the number of times it’s repeated, then the character.
replace_wrep: Replaces any word repeated three times or more with a special token for word repetition (xxwrep), the number of times it’s repeated, then the character.
spec_add_spaces: adds spaces around / and #.
rm_useless_spaces: Removes all repetitions of the space character.
replace_all_caps: Lowercases a word written in all caps and adds a special token for all caps (xxcap) in front of it.
replace_maj: Lowercases a capitalized word and adds a special token for capitalized (xxmaj) in front of it.
lowercase: Lowercases all text and adds a special token at the beginning (xxbos) and/or the end (xxeos).
coll_repr(tkn("© Fast.ai www.fast.ai/INDEX"), 31)"(#11) ['xxbos','©','xxmaj','fast.ai','xxrep','3','w','.fast.ai','/','xxup','index']"Subword Tokenization
Word tokenization relies on an assumption that spaces provide a useful separation of components of meaning in a sentence. However this assumption is not always appropriate. Languages like Chinese and Japanese don’t use spaces. Turkish and Hungarian can add many subwords together without spaces.
Two steps of subword tokenization:
- Analyze a corpus of documents to find the most commonly occuring groups of letters. These becomes the vocab.
- Tokenize the corpus string using this vocab of subword units.
txts = L(o.open().read() for o in files[:2000])! pip install sentencepiece
def subword(sz):
sp = SubwordTokenizer(vocab_sz=sz)
sp.setup(txts)
return ' '.join(first(sp([txt]))[:40])setup reads the documents and finds the common sequences of characters to create the vocab.
subword(1000)"▁De s p ite ▁some ▁humor ous ▁b ant er ▁and ▁a ▁de cent ▁support ing ▁cast , ▁I ▁can ' t ▁really ▁recommend ▁this ▁movie . ▁The ▁lead s ▁are n ' t ▁very ▁li k able ▁and ▁I"When using fastai’s subword tokenizer, _ represents a space character in the original text.
If we use a smaller vocab, each token will represent fewer characters and it will take more tokens to represent a sentence.
subword(200)'▁ D es p it e ▁ s o m e ▁h u m or o us ▁b an ter ▁and ▁a ▁ d e c ent ▁ s u p p or t ing ▁ c a s t'If we use a larger vocab, most common English words will end up in the vocab themselves, and we will not need as many to represent a sentence:
subword(10000)"▁Des pite ▁some ▁humorous ▁ban ter ▁and ▁a ▁decent ▁support ing ▁cast , ▁I ▁can ' t ▁really ▁recommend ▁this ▁movie . ▁The ▁leads ▁are n ' t ▁very ▁likable ▁and ▁I ▁didn ' t ▁particular ly ▁care ▁if ▁they"A larger vocab means fewer tokens per sentence, which means faster training, less memory and less state for the model to remember; but on the downside, it means larger embedding matricces, which require more data to learn.
Subword tokenization provides a way to easily scale between character tokenization (using a small subword vocab) and word tokenization (using a large subword vocab) and handles every human language. It can even handle genomic sequences or MIDI music notation. It’s likely to become (or has already) the most common tokenization approach.
Numericalization with fast.ai
Numericalization is the process of mapping tokens to integers.
- Make a list of all possible levels of the categorical variable (the vocab).
- Replace each level with its index in the vocab.
toks = tkn(txt)
print(coll_repr(tkn(txt), 31))(#264) ['xxbos','xxmaj','despite','some','humorous','banter','and','a','decent','supporting','cast',',','i','ca',"n't",'really','recommend','this','movie','.','xxmaj','the','leads','are',"n't",'very','likable','and','i','did',"n't"...]Just like with SubwordTokenizer, we need to call setup on Numericalize to create the vocab. That means we’ll need our tokenized corpus first:
toks200 = txts[:200].map(tkn)
toks200[0](#264) ['xxbos','xxmaj','despite','some','humorous','banter','and','a','decent','supporting'...]num = Numericalize()
num.setup(toks200)
coll_repr(num.vocab, 20)"(#2200) ['xxunk','xxpad','xxbos','xxeos','xxfld','xxrep','xxwrep','xxup','xxmaj','the','.',',','and','a','of','to','is','in','i','it'...]"Our special rules tokens appear first, and then every word appears once in frequency order.
The defaults to Numericalize are min_freq=3 and max_vocab=60000. max_vocab results in fastai replacing all words other than the most common 60,000 with a special unknown word token, xxunk. This is useful to avoid having an overly large embedding matrix, since that can slow down training and use up too much memory, and can also mean that there isn’t enough data to train useful representations for rare words (better handles by setting min_freq, any word appearing fewer than it is replaced with xxunk).
fastai can also numericalize your dataset using a vocab that you provide, by passing a list of words as the vocab parameter.
The Numericalizer object is used like a function:
nums = num(toks)[:20]; numsTensorText([ 2, 8, 418, 68, 0, 0, 12, 13, 618, 419, 190, 11, 18,
259, 38, 93, 445, 21, 28, 10])We can check that the integers map back to the original text:
' '.join(num.vocab[o] for o in nums)"xxbos xxmaj despite some xxunk xxunk and a decent supporting cast , i ca n't really recommend this movie ."Putting Our Texts into Batches for a Language Model
We want our language model to read text in order, so that it can efficiently predict what the next word is, this means each new batch should begin precisely where the previous one left off.
At the beginning of each epoch we will shuffle the order of the documents to make a new stream.
We then cut this stream into a certain number of batches (which is our batch size). For example, if the stream has 50,000 tokens as we set a batch size of 10, this will give us 10 mini-streams of 5,000 tokens. What is important is that we preserve the order of the tokens (1 to 5,000 for the first mini-stream, then from 5,001 to 10,000…) because we want the model to read continuous rows of text. An xxbos token is added at the start of each text during preprocessing, so that the model knowns when it reads the stream when a new entry is beginning.
First apply our Numericalize object to the tokenized texts:
nums200 = toks200.map(num)Then pass it to the LMDataLoader:
dl = LMDataLoader(nums200)x,y = first(dl)
x.shape, y.shape(torch.Size([64, 72]), torch.Size([64, 72]))x[:1], y[:1](LMTensorText([[ 2, 8, 418, 68, 0, 0, 12, 13, 618, 419, 190,
11, 18, 259, 38, 93, 445, 21, 28, 10, 8, 9,
693, 42, 38, 72, 1274, 12, 18, 81, 38, 479, 420,
58, 47, 305, 274, 17, 9, 135, 10, 18, 619, 81,
38, 49, 9, 221, 120, 221, 47, 305, 274, 11, 29,
8, 0, 8, 1275, 783, 74, 59, 446, 15, 43, 9,
0, 285, 114, 0, 24, 0]]),
TensorText([[ 8, 418, 68, 0, 0, 12, 13, 618, 419, 190, 11,
18, 259, 38, 93, 445, 21, 28, 10, 8, 9, 693,
42, 38, 72, 1274, 12, 18, 81, 38, 479, 420, 58,
47, 305, 274, 17, 9, 135, 10, 18, 619, 81, 38,
49, 9, 221, 120, 221, 47, 305, 274, 11, 29, 8,
0, 8, 1275, 783, 74, 59, 446, 15, 43, 9, 0,
285, 114, 0, 24, 0, 30]]))Looking at the first row of the independent variable:
' '.join(num.vocab[o] for o in x[0][:20])"xxbos xxmaj despite some xxunk xxunk and a decent supporting cast , i ca n't really recommend this movie ."Which is the start of the text.
The dependent variable is the same thing offset by one token:
' '.join(num.vocab[o] for o in y[0][:20])"xxmaj despite some xxunk xxunk and a decent supporting cast , i ca n't really recommend this movie . xxmaj"We are now ready to train our text classifier.
Training a Text Classifier
Two steps to training a state-of-the-art text classifier using transfer learning:
- Fine-tune our language model pretrained on Wikipedia to the corpus of IMDb reviews.
- Use that model to train a classifier.
Language Model Using DataBlock
fastai handles tokenization and numericalization automatically when TextBlock is passed to DataBlock.
get_imdb = partial(get_text_files, folders=['train', 'test', 'unsup'])
dls_lm = DataBlock(
blocks=TextBlock.from_folder(path, is_lm=True),
get_items=get_imdb,
splitter=RandomSplitter(0.1)
).dataloaders(path, path=path, bs=128, seq_len=80)from_folder tells TextBlock how to access the texts so that it can do initial preprocessing. fastai performs a few optmizations:
- It saves the tokenized documents in a temporary folder, so it doesn’t have to tokenize them more than once.
- It runs multiple tokenization processes in parallel, to take advantage of your computer’s CPUs.
dls_lm.show_batch(max_n=2)| text | text_ | |
|---|---|---|
| 0 | xxbos xxmaj caught this at xxmaj cinequest . xxmaj it was well attended , but the crowd seemed disappointed . xxmaj in my humble opinion , " charlie the xxmaj ox " was very amateurish and overrated ( it pales in comparison with other cinequest pics i saw ) . xxmaj acting ( with the exception of xxmaj polito ) seemed self - conscious and " stagey . " xxmaj photography , despite originating on high - end xxup hd | xxmaj caught this at xxmaj cinequest . xxmaj it was well attended , but the crowd seemed disappointed . xxmaj in my humble opinion , " charlie the xxmaj ox " was very amateurish and overrated ( it pales in comparison with other cinequest pics i saw ) . xxmaj acting ( with the exception of xxmaj polito ) seemed self - conscious and " stagey . " xxmaj photography , despite originating on high - end xxup hd , |
| 1 | career , seemed to specialize in patriarch roles , such as in " all the xxmaj president 's xxmaj men " , " max xxmaj dugan xxmaj returns " , and " you xxmaj ca n't xxmaj take it xxmaj with xxmaj you " . xxmaj and in this case , those of us who never saw him on the stage get a big treat , because this was a taped xxmaj broadway production . xxmaj he dominates every scene | , seemed to specialize in patriarch roles , such as in " all the xxmaj president 's xxmaj men " , " max xxmaj dugan xxmaj returns " , and " you xxmaj ca n't xxmaj take it xxmaj with xxmaj you " . xxmaj and in this case , those of us who never saw him on the stage get a big treat , because this was a taped xxmaj broadway production . xxmaj he dominates every scene , |
Each item in the training dataset is a document:
' '.join(dls_lm.vocab[o] for o in dls_lm.train.dataset[0][0])"xxbos xxmaj it is a delight to watch xxmaj laurence xxmaj harvey as a neurotic chess player , who schemes to murder the opponent he can not defeat at the chessboard . xxmaj this movie has wonderful pacing and several cliffhanger moments , as xxmaj harvey 's plot several times seems on the point of failure or exposure , but he manages to beat the odds yet again . xxmaj columbo wages a skilful war of nerves against this high - strung genius , and the scene where he manages to rattle him enough to cause him to make a mistake while playing chess is one of the highlights of the movie , as xxmaj harvey looks down in disbelief at the board , where he has just allowed himself to be xxunk . xxmaj the climax is almost as strong , and watching xxmaj laurence xxmaj harvey collapse completely as his scheme is exposed brings the movie to a satisfying finish . xxmaj highly recommended ."' '.join(dls_lm.vocab[o] for o in dls_lm.train.dataset[2][0])"xxbos xxmaj eyeliner was worn nearly 6 xxrep 3 0 years ago in xxmaj egypt . xxmaj really not that much of a stretch for it to be around in the 12th century . i also did n't realize the series flopped . xxmaj there is a second season airing now is n't there ? xxmaj it is amazing to me when commentaries are made by those who are either ill - informed or do n't watch a show at all . xxmaj it is a waste of space on the boards and of other 's time . xxmaj the first show of the series was maybe a bit painful as the cast began to fall into place , but that is to be expected from any show . xxmaj the remainder of the first season is excellent . i can hardly wait for the second season to begin in the xxmaj united xxmaj states ."To confirm my understanding, that the first item in each batch is continuing the mini-stream, I’ll take a look at the first mini-stream of the first two batches:
counter = 0
for xb, yb in dls_lm.train:
output = ' '.join(dls_lm.vocab[o] for o in xb[0])
print(output)
counter += 1
if counter == 2: breakxxbos xxmaj just got this in the mail and i was positively surprised . xxmaj as a big fan of 70 's cinema it does n't take much to satisfy me when it comes to these kind of flicks . xxmaj despite the obvious low budget on this movie , the acting is overall good and you can already see why xxmaj pesci was to become on of the greatest actors ever . xxmaj i 'm not sure how authentic
this movie is , but it sure is a good contribution to the mob genre … .. xxbos xxmaj why on earth should you explore the mesmerizing nature documentary " earth " ? xxmaj how much time do you have on earth so i can explain this to you ? xxup ok , i will not xxunk my review exploration on " earth " to infinity , but i must stand my ground on why this is a " mustConfirmed! The second batch’s first mini-stream is a continuation of the first batch’s first mini-stream. In this case, the first mini-stream of the second batch also contains the start of the next movie review (document) as indicated by the xxbos special token.
Fine-Tuning the Language Model
To convert the integer word indices into activations that we can use for our neural network, we will use embeddings. We feed those embeddings into a recurrent neural network (RNN) using an architecture called AWS-LSTM.
The embeddings in the pretrained model are merged with random embeddings added for words that weren’t in the pretraining vocabulary.
learn = language_model_learner(
dls_lm,
AWD_LSTM,
drop_mult=0.3,
metrics=[accuracy, Perplexity()]
).to_fp16()The loss function used by default is cross-entropy loss, since we essentially have a classification problem (the different categories being the words in our vocab).
Perplexity is a metric often used in NLP for language models. It is the exponential of loss (i.e., torch.exp(cross_entropy)).
language_model_learner automatically calls freeze when using a pretrained model (which is the default) so this will train only the embeddings (the part of the model that contains randomly initialized weights—embeddings for the words that are in our IMDb vocab, but aren’t in the pretrained model vocab).
I wasn’t able to train my model on Google Colab (I got a ran out of memory error even for small batches) so I trained the IMDb language model on Paperspace and wrote a separate blog post about it.
Disinformation and Language Models
- Even simple algorithms could be used to create fraudulent accounts and try to influence policymakers (99% of the 2017 Net Neutrality public comments were likely faked).
- Many people assume or hope that algorithms will come to our defense here, the problem is that this will always be an arms race, in which better classification (or discriminator) algorithms can be used to create better generation algorithms.
Questionnaire
1. What is self-supervised learning?
Self-supervised learning is when you train a model on data that does not contain any external labels. Instead, the labels are embedded in the independent variable.
2. What is a language model?
A language model is a model that predicts the next word based on the previous words in a text.
3. Why is a language model considered self-supervised?
Because we do not train the model with external labels. The dependent variable is the next token in a sequence of previous tokens (independent variable).
4. What are self-supervised models usually used for?
Pretraining a model that will be used for transfer learning.
5. Why do we fine-tune language models?
In order for it to learn the style of language used in our specific corpus.
6. What are the three steps to create a state-of-the-art text classifier?
- Train a language model on a large general corpus like Wikipedia.
- Fine-tune a language model using your task-specific corpus.
- Fine-tune a classifier using the encoder of the twice-pretrained language model.
7. How do the 50,000 unlabeled movie reviews help create a better text classifier for the IMDb dataset?
The 50k unlabeled movie reviews help create a better text classifier for the IMDb dataset because when you fine-tune the pretrained Wikipedia language model using this data, the model learns the particular style and content of IMDb movie reviews, which helps it better understand what the language used in the reviews means when classifying it as positive or negative.
8. What are the three steps to prepare your data for a language model?
- Tokenization: convert the text into a list of words (or characters or substrings).
- Numericalization: List all of the words that appear (the vocab) and convert each word into a number by looking up its index in the vocab.
- Language model data loader creation: combine the documents into one string and split it into fixed sequence length batches while preserving the order of the tokens, create a dependent variable that is offset from the independent variable by one token, and shuffle the training data (maintaining independent/dependent variable structure).
9. What is tokenization? Why do we need it?
Tokenization is the conversion of text into smaller parts (like words, subwords or characters). In order to convert our documents into numbers (categories) that the language model can learn something about, we first tokenize them (break them into smaller parts) so that we can generate a list of unique tokens (unique levels of a categorical variable) contained in the corpus (categorical variable).
10. Name three approaches to tokenization.
- word-based: split a sentence based on spaces.
- subword based: split words into commonly occurring substrings.
- character-based: split a sentence into its individual characters.
11. What is xxbos?
A special token that tells the language model that we are at the start of a new stream (document).
12. List four rules that fastai applies to text during tokenization.
I’ll list them all:
fix_html: replace special HTML characters (like©—the copyright symbol) with a readable version.replace_rep: replace repeated characters with a special token for repetition (xxrep), the number of times it’s repeated, and then the character.replace_wrep: do the same asreplace_repbut for repeated words (using the special tokenxxwrep).spec_add_spaces: add spaces around/and#.rm_useless_spaces: remove all repetitions of the space character.replace_all_caps: lowercase all-caps words and place a special tokenxxcapin front of it.replace_maj: lowercase a capitalized word and place a special tokenxxmajin front of it.lowercase: lowercase all text and place a special token at the beginning (xxbos) and/or at the end (xxeos).
13. Why are repeated characters replaced with a token showing the number of repetitions and the character that’s repeated?
So that the model’s embedding matrix can encode information about general concepts such as repeated punctuation without requiring a unique token for every number of repetitions of a character.
14. What is numericalization?
Converting a token to a number by looking up its index in the vocab (unique list of all tokens).
15. Why might there be words that are replaced with the “unknown word” token?
In order to avoid having an overly large embedding matrix, fastai’s numericalization replaces two types of words with with the unknown word token xxunk:
- Words that appear less than
min_freqtimes. - Words that are not in the
max_vocabmost frequent words.
For example, if min_freq = 3 then all words that appear once or twice are replaced with xxunk.
If max_vocab = 60000 then words the appear less frequently than the 60000th most frequent word are replaced with xxunk.
16. With a batch size of 64, the first row of the tensor representing the first batch contains the first 64 tokens for the dataset. What does the second row of that tensor contain?
The second row contains 64 tokens of the (n/b/s+1)th group of tokens where n is the number of tokens, divided by the number of batches b divided by the sequence length s. So, if we have 90 tokens divided into 6 batches (rows) with a sequence length (columns) of 5, then the second row of the first batch contains the 4th (i.e., 3 + 1) group of tokens.
Putting Tanishq’s answer here as well:
The dataset is split into 64 mini-streams (batch size).
Each batch has 64 rows (batch size) and 64 columns (sequence length).
The first row of the first batch contains the beginning of the first mini-stream (tokens 1-64).
The second row of the first batch contains the beginning of the second mini-stream.
The first row of the second batch contains the second chunk of the first mini-stream (tokens 65 - 128).
17. Why do we need padding for text classification? Why don’t we need it for language modeling?
When the data is prepared for language modeling, the documents are concatenated into a single string and broken up into equally-sized batches, so there is no need to pad any batches—they’re already the right size.
In the case of text classification, each document is maintained in full length in a batch, and documents will very likely have a varying number of tokens (i.e., everyone is not writing the same length of movie reviews with the same number of special tokens) so in each batch, all of the documents (except the largest) will need to be padded to the batch’s largest document’s size. fastai sorts the data by length each epoch and groups together documents of similar lengths for each batch before applying the padding.
Something that I would like to understand however is:
What if the number of tokens in the training dataset is not divisible by the selected batch size and sequence length? Does fastai use padding in that case? Suppose you have 1000 tokens in total, a batch size of 16 and sequence length of 20. 320 goes into 1000 3 times with a remainder. Does fastai create a 4th batch with padding? Or remove the tokens so there’s only 3 batches? I’ll see if I can figure out what it does with some sample code:
bs,sl = 5, 2
ints = L([[0,1,2,3,4,5,6,7,8,9,10,11,12,13]]).map(tensor)dl = LMDataLoader(ints, bs=bs, seq_len=sl)
list(dl)[(LMTensorText([[0, 1],
[2, 3],
[4, 5],
[6, 7],
[8, 9]]),
tensor([[ 1, 2],
[ 3, 4],
[ 5, 6],
[ 7, 8],
[ 9, 10]]))]list(LMDataLoader(ints, bs=bs, seq_len=sl, drop_last=False))[(LMTensorText([[0, 1],
[2, 3],
[4, 5],
[6, 7],
[8, 9]]),
tensor([[ 1, 2],
[ 3, 4],
[ 5, 6],
[ 7, 8],
[ 9, 10]]))]Looks like fastai drops the last batch if it’s not full. I’ve posted this question in the fastai forums to get a confirmation on my understanding.
18. What does an embedding matrix for NLP contain? What is its shape?
It contains the parameters that are trained by the neural net, with each parameter corresponding to each token in the vocab.
From Tanishq’s solutions:
The embedding matrix has the size (vocab_size x embedding_size) where vocab_size is the length of the vocabulary, and embedding_size is an arbitrary number defining the number of latent factors of the tokens.
19. What is perplexity?
A metric used in NLP. It is the exponential of the loss.
20. Why do we have to pass the vocabulary of the language model to the classifier data block?
The indexes corresponding to the tokens have to be maintained because we are fine-tuning the language model.
21. What is gradual unfreezing?
When we train one layer at a time for one epoch before we unfreeze and train the full model (including all layers of the encoder).
22. Why is text generation always likely to be ahead of automatic identification of machine-generated texts?
Because text generation models can be trained to beat automatic identification algorithms.
Further Research
1. See what you can learn about language models and disinformation. What are the best language models today? Take a look at some of their outputs. Do you find them convincing? How could a bad actor best use such a model to create conflict and uncertainty?
- Here is a tweet thread by Arvind Narayan talking about how the danger of ChatGPT is that “you can’t tell when it’s wrong unless you already know the answer”.
- This New York Times article walks through different examples of ChatGPT responding to prompts with disinformation.
- This NewsGuard article, which was referenced in the NYT article, discusses how ChatGPT-4 is more prone to perpetuating misinformation than its predecessor GPT-3.5. GPT-3.5 generated 80 of 100 false narratives given as prompts while GPT-4 generated 100 of 100 false narratives. Also, “ChatGPT-4’s responses that contained false and misleading claims were less likely to include disclaimers about the falsity of those claims (23% of the time) [than ChatGPT-3.5 (51% of the time)].
- This NBC New York article walks through an example of how a ChatGPT written story on Michael Bloomberg was full of made-up quotes and sources. It also talks about how some educators are embracing ChatGPT in the classroom, and while ineffective, there are machine-generated text identification algorithms available. Although it’s important to note, as disussed in the fastai course, that text generation models will always be ahead of automatic identification models (generative models can be trained to beat identification models).
- In this Harvard Business School Working Knowledge article Scott Van Voorhiss and Tsedal Neeley summarise the story of how Dr. Timnit Gebru went from Ethiopia, to Boston, to a PhD at Stanford, and co-lead of Google AI Ethics, later to be fired when because she co-authored a paper that asked for companies to hold off on building large language models until we figured out how to handle the bias perpetuated by these models.
The article’s authors use these events as a case study to learn from when handling issues of ethics in AI.
- “The biggest message I want to convey is that AI can scale bias in ways that we can barely understand today”.
- “in failing to give Gebru the independence to do her job, might have sacrificed an opportunity to become a global leader in responsible AI development”.
- Finally, in this paper the authors test detection tools for AI-generated text in academic settings. “The researchers conclude that the available detection tools are neither accurate nor reliable and have a main bias towards classifying the output as human-written rather than detecting AI-generated text”. Across the 14 tools, the highest average accuracy was less than 80%, with 50% for AI-generated/human-edited text and 26% for machine-paraphrased AI-generated text.
2. Given the limitation that models are unlikely to be able to consistently recognize machine-generated texts, what other approaches may be needed to handle large-scale disinformation campaigns that leverage deep learning?
The first thing that comes to mind is Glaze by the University of Chicago which “works by understanding the AI models that are training on human art, and using machine learning algorithms, computing a set of minimal changes to artworks, such that it appears unchanged to human eyes, but appears to AI models like a dramatically different art style…So when someone then prompts the model to generate art mimicking the charcoal artist, they will get something quite different from what they expected.”
I can’t imagine how something analogous to Glaze can be created for language, since plain text is just plain text, but conceptually, if human-written language is altered in a similar way, then it will be prevented from being generated similarly by LLMs like GPT. This would effect not just LLMs but anyone training their model on such altered data, but perhaps that is a cost worth having to prevent the perpetuation of copyrighted or disinformation content.
Another idea is that disinformation detection may benefit from a human-in-the-loop. AI-generated content that is not identified automatically may be identified by a human as disinformation. A big enough sample of accounts spreading this misinformation may lead to identifying broader trends in which accounts are fake.
Lesson 5: From-scratch Model
Notebook Exercise: Linear model and neural net from scratch
In this section I’ll run code cells from the “clean” version (no markdown or outputs) of this notebook by Jeremy. I’ll add some thoughts as I run cells and add code to understand what is going on.
from pathlib import Path
cred_path = Path('~/.kaggle/kaggle.json').expanduser()
if not cred_path.exists():
cred_path.parent.mkdir(exist_ok=True)
cred_path.write_text(creds)
cred_path.chmod(0o600)import os
iskaggle = os.environ.get('KAGGLE_KERNEL_RUN_TYPE', '')
if iskaggle: path = Path("../input/titanic")
else:
path = Path('titanic')
if not path.exists():
import zipfile, kaggle
kaggle.api.competition_download_cli(str(path))
zipfile.ZipFile(f'{path}.zip').extractall(path)Downloading titanic.zip to /content100%|██████████| 34.1k/34.1k [00:00<00:00, 2.77MB/s]import torch, numpy as np, pandas as pd
np.set_printoptions(linewidth=140)
torch.set_printoptions(linewidth=140, sci_mode=False, edgeitems=7)
pd.set_option('display.width', 140)# load the training data and look at it
df = pd.read_csv(path/'train.csv')
df| PassengerId | Survived | Pclass | Name | Sex | Age | SibSp | Parch | Ticket | Fare | Cabin | Embarked | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 1 | 0 | 3 | Braund, Mr. Owen Harris | male | 22.0 | 1 | 0 | A/5 21171 | 7.2500 | NaN | S |
| 1 | 2 | 1 | 1 | Cumings, Mrs. John Bradley (Florence Briggs Th... | female | 38.0 | 1 | 0 | PC 17599 | 71.2833 | C85 | C |
| 2 | 3 | 1 | 3 | Heikkinen, Miss. Laina | female | 26.0 | 0 | 0 | STON/O2. 3101282 | 7.9250 | NaN | S |
| 3 | 4 | 1 | 1 | Futrelle, Mrs. Jacques Heath (Lily May Peel) | female | 35.0 | 1 | 0 | 113803 | 53.1000 | C123 | S |
| 4 | 5 | 0 | 3 | Allen, Mr. William Henry | male | 35.0 | 0 | 0 | 373450 | 8.0500 | NaN | S |
| ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... |
| 886 | 887 | 0 | 2 | Montvila, Rev. Juozas | male | 27.0 | 0 | 0 | 211536 | 13.0000 | NaN | S |
| 887 | 888 | 1 | 1 | Graham, Miss. Margaret Edith | female | 19.0 | 0 | 0 | 112053 | 30.0000 | B42 | S |
| 888 | 889 | 0 | 3 | Johnston, Miss. Catherine Helen "Carrie" | female | NaN | 1 | 2 | W./C. 6607 | 23.4500 | NaN | S |
| 889 | 890 | 1 | 1 | Behr, Mr. Karl Howell | male | 26.0 | 0 | 0 | 111369 | 30.0000 | C148 | C |
| 890 | 891 | 0 | 3 | Dooley, Mr. Patrick | male | 32.0 | 0 | 0 | 370376 | 7.7500 | NaN | Q |
891 rows × 12 columns
# see how many null values are in each column
df.isna().sum()PassengerId 0
Survived 0
Pclass 0
Name 0
Sex 0
Age 177
SibSp 0
Parch 0
Ticket 0
Fare 0
Cabin 687
Embarked 2
dtype: int64Since each Name is unique, there are 891 modes for the Name column. df.mode() will print these out as a DataFrame, with rows containing NaN for columns with fewer modes (e.g., Age has 1 mode, 24, and that is listed once in the first row in the output DataFrame for df.mode()).
# see the most frequent values in each column
df.mode()| PassengerId | Survived | Pclass | Name | Sex | Age | SibSp | Parch | Ticket | Fare | Cabin | Embarked | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 1 | 0.0 | 3.0 | Abbing, Mr. Anthony | male | 24.0 | 0.0 | 0.0 | 1601 | 8.05 | B96 B98 | S |
| 1 | 2 | NaN | NaN | Abbott, Mr. Rossmore Edward | NaN | NaN | NaN | NaN | 347082 | NaN | C23 C25 C27 | NaN |
| 2 | 3 | NaN | NaN | Abbott, Mrs. Stanton (Rosa Hunt) | NaN | NaN | NaN | NaN | CA. 2343 | NaN | G6 | NaN |
| 3 | 4 | NaN | NaN | Abelson, Mr. Samuel | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN |
| 4 | 5 | NaN | NaN | Abelson, Mrs. Samuel (Hannah Wizosky) | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN |
| ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... |
| 886 | 887 | NaN | NaN | de Mulder, Mr. Theodore | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN |
| 887 | 888 | NaN | NaN | de Pelsmaeker, Mr. Alfons | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN |
| 888 | 889 | NaN | NaN | del Carlo, Mr. Sebastiano | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN |
| 889 | 890 | NaN | NaN | van Billiard, Mr. Austin Blyler | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN |
| 890 | 891 | NaN | NaN | van Melkebeke, Mr. Philemon | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN |
891 rows × 12 columns
# view the topmost row of the modes DataFrame
modes = df.mode().iloc[0]
modesPassengerId 1
Survived 0.0
Pclass 3.0
Name Abbing, Mr. Anthony
Sex male
Age 24.0
SibSp 0.0
Parch 0.0
Ticket 1601
Fare 8.05
Cabin B96 B98
Embarked S
Name: 0, dtype: object# fill missing data with the column's mode
df.fillna(modes, inplace=True)# check that we no longer have missing data
df.isna().sum()PassengerId 0
Survived 0
Pclass 0
Name 0
Sex 0
Age 0
SibSp 0
Parch 0
Ticket 0
Fare 0
Cabin 0
Embarked 0
dtype: int64import numpy as np
# view a summary of the data
df.describe(include=(np.number))| PassengerId | Survived | Pclass | Age | SibSp | Parch | Fare | |
|---|---|---|---|---|---|---|---|
| count | 891.000000 | 891.000000 | 891.000000 | 891.000000 | 891.000000 | 891.000000 | 891.000000 |
| mean | 446.000000 | 0.383838 | 2.308642 | 28.566970 | 0.523008 | 0.381594 | 32.204208 |
| std | 257.353842 | 0.486592 | 0.836071 | 13.199572 | 1.102743 | 0.806057 | 49.693429 |
| min | 1.000000 | 0.000000 | 1.000000 | 0.420000 | 0.000000 | 0.000000 | 0.000000 |
| 25% | 223.500000 | 0.000000 | 2.000000 | 22.000000 | 0.000000 | 0.000000 | 7.910400 |
| 50% | 446.000000 | 0.000000 | 3.000000 | 24.000000 | 0.000000 | 0.000000 | 14.454200 |
| 75% | 668.500000 | 1.000000 | 3.000000 | 35.000000 | 1.000000 | 0.000000 | 31.000000 |
| max | 891.000000 | 1.000000 | 3.000000 | 80.000000 | 8.000000 | 6.000000 | 512.329200 |
So that it’s more normally distributed, we take the log of Fare. We add 1 to Fare before taking the logarithm so that we aren’t ever taking log of 0 (which is undefined).
df['LogFare'] = np.log(df['Fare']+1)# view the unique values of pclass
pclasses = sorted(df.Pclass.unique())
pclasses[1, 2, 3]# look at string columns
df.describe(include=[object])| Name | Sex | Ticket | Cabin | Embarked | |
|---|---|---|---|---|---|
| count | 891 | 891 | 891 | 891 | 891 |
| unique | 891 | 2 | 681 | 147 | 3 |
| top | Braund, Mr. Owen Harris | male | 347082 | B96 B98 | S |
| freq | 1 | 577 | 7 | 691 | 646 |
# get_dummies returns DataFrame with 0/1 values for categorical variable columns
df = pd.get_dummies(df, columns=['Sex', 'Pclass', 'Embarked'])
df.columnsIndex(['PassengerId', 'Survived', 'Name', 'Age', 'SibSp', 'Parch', 'Ticket', 'Fare', 'Cabin', 'LogFare', 'Sex_female', 'Sex_male',
'Pclass_1', 'Pclass_2', 'Pclass_3', 'Embarked_C', 'Embarked_Q', 'Embarked_S'],
dtype='object')# view the new dummy variables
added_cols = ['Sex_male', 'Sex_female', 'Pclass_1', 'Pclass_2', 'Pclass_3', 'Embarked_C', 'Embarked_Q', 'Embarked_S']
df[added_cols].head()| Sex_male | Sex_female | Pclass_1 | Pclass_2 | Pclass_3 | Embarked_C | Embarked_Q | Embarked_S | |
|---|---|---|---|---|---|---|---|---|
| 0 | 1 | 0 | 0 | 0 | 1 | 0 | 0 | 1 |
| 1 | 0 | 1 | 1 | 0 | 0 | 1 | 0 | 0 |
| 2 | 0 | 1 | 0 | 0 | 1 | 0 | 0 | 1 |
| 3 | 0 | 1 | 1 | 0 | 0 | 0 | 0 | 1 |
| 4 | 1 | 0 | 0 | 0 | 1 | 0 | 0 | 1 |
from torch import tensor
# convert dependent variable to a tensor
t_dep = tensor(df.Survived)
t_dep[:5]tensor([0, 1, 1, 1, 0])# convert independent variables to a tensor
indep_cols = ['Age', 'SibSp', 'Parch', 'LogFare'] + added_cols
indep_cols['Age',
'SibSp',
'Parch',
'LogFare',
'Sex_male',
'Sex_female',
'Pclass_1',
'Pclass_2',
'Pclass_3',
'Embarked_C',
'Embarked_Q',
'Embarked_S']df[indep_cols].valuesarray([[22., 1., 0., ..., 0., 0., 1.],
[38., 1., 0., ..., 1., 0., 0.],
[26., 0., 0., ..., 0., 0., 1.],
...,
[24., 1., 2., ..., 0., 0., 1.],
[26., 0., 0., ..., 1., 0., 0.],
[32., 0., 0., ..., 0., 1., 0.]])t_indep = tensor(df[indep_cols].values, dtype=torch.float)
t_indeptensor([[22.0000, 1.0000, 0.0000, 2.1102, 1.0000, 0.0000, 0.0000, 0.0000, 1.0000, 0.0000, 0.0000, 1.0000],
[38.0000, 1.0000, 0.0000, 4.2806, 0.0000, 1.0000, 1.0000, 0.0000, 0.0000, 1.0000, 0.0000, 0.0000],
[26.0000, 0.0000, 0.0000, 2.1889, 0.0000, 1.0000, 0.0000, 0.0000, 1.0000, 0.0000, 0.0000, 1.0000],
[35.0000, 1.0000, 0.0000, 3.9908, 0.0000, 1.0000, 1.0000, 0.0000, 0.0000, 0.0000, 0.0000, 1.0000],
[35.0000, 0.0000, 0.0000, 2.2028, 1.0000, 0.0000, 0.0000, 0.0000, 1.0000, 0.0000, 0.0000, 1.0000],
[24.0000, 0.0000, 0.0000, 2.2469, 1.0000, 0.0000, 0.0000, 0.0000, 1.0000, 0.0000, 1.0000, 0.0000],
[54.0000, 0.0000, 0.0000, 3.9677, 1.0000, 0.0000, 1.0000, 0.0000, 0.0000, 0.0000, 0.0000, 1.0000],
...,
[25.0000, 0.0000, 0.0000, 2.0857, 1.0000, 0.0000, 0.0000, 0.0000, 1.0000, 0.0000, 0.0000, 1.0000],
[39.0000, 0.0000, 5.0000, 3.4054, 0.0000, 1.0000, 0.0000, 0.0000, 1.0000, 0.0000, 1.0000, 0.0000],
[27.0000, 0.0000, 0.0000, 2.6391, 1.0000, 0.0000, 0.0000, 1.0000, 0.0000, 0.0000, 0.0000, 1.0000],
[19.0000, 0.0000, 0.0000, 3.4340, 0.0000, 1.0000, 1.0000, 0.0000, 0.0000, 0.0000, 0.0000, 1.0000],
[24.0000, 1.0000, 2.0000, 3.1966, 0.0000, 1.0000, 0.0000, 0.0000, 1.0000, 0.0000, 0.0000, 1.0000],
[26.0000, 0.0000, 0.0000, 3.4340, 1.0000, 0.0000, 1.0000, 0.0000, 0.0000, 1.0000, 0.0000, 0.0000],
[32.0000, 0.0000, 0.0000, 2.1691, 1.0000, 0.0000, 0.0000, 0.0000, 1.0000, 0.0000, 1.0000, 0.0000]])# 891 individuals
# 12 columns
t_indep.shapetorch.Size([891, 12])# initialize parameters
torch.manual_seed(442)
n_coeff = t_indep.shape[1]
coeffs = torch.rand(n_coeff)-0.5
coeffstensor([-0.4629, 0.1386, 0.2409, -0.2262, -0.2632, -0.3147, 0.4876, 0.3136, 0.2799, -0.4392, 0.2103, 0.3625])coeffs.shapetorch.Size([12])# normalize large values
t_indep.max(dim=0)torch.return_types.max(
values=tensor([80.0000, 8.0000, 6.0000, 6.2409, 1.0000, 1.0000, 1.0000, 1.0000, 1.0000, 1.0000, 1.0000, 1.0000]),
indices=tensor([630, 159, 678, 258, 0, 1, 1, 9, 0, 1, 5, 0]))vals, indices = t_indep.max(dim=0)
# divide values in each column by the maximum in each column
# using broadcasting
t_indep = t_indep / vals
t_indeptensor([[0.2750, 0.1250, 0.0000, 0.3381, 1.0000, 0.0000, 0.0000, 0.0000, 1.0000, 0.0000, 0.0000, 1.0000],
[0.4750, 0.1250, 0.0000, 0.6859, 0.0000, 1.0000, 1.0000, 0.0000, 0.0000, 1.0000, 0.0000, 0.0000],
[0.3250, 0.0000, 0.0000, 0.3507, 0.0000, 1.0000, 0.0000, 0.0000, 1.0000, 0.0000, 0.0000, 1.0000],
[0.4375, 0.1250, 0.0000, 0.6395, 0.0000, 1.0000, 1.0000, 0.0000, 0.0000, 0.0000, 0.0000, 1.0000],
[0.4375, 0.0000, 0.0000, 0.3530, 1.0000, 0.0000, 0.0000, 0.0000, 1.0000, 0.0000, 0.0000, 1.0000],
[0.3000, 0.0000, 0.0000, 0.3600, 1.0000, 0.0000, 0.0000, 0.0000, 1.0000, 0.0000, 1.0000, 0.0000],
[0.6750, 0.0000, 0.0000, 0.6358, 1.0000, 0.0000, 1.0000, 0.0000, 0.0000, 0.0000, 0.0000, 1.0000],
...,
[0.3125, 0.0000, 0.0000, 0.3342, 1.0000, 0.0000, 0.0000, 0.0000, 1.0000, 0.0000, 0.0000, 1.0000],
[0.4875, 0.0000, 0.8333, 0.5456, 0.0000, 1.0000, 0.0000, 0.0000, 1.0000, 0.0000, 1.0000, 0.0000],
[0.3375, 0.0000, 0.0000, 0.4229, 1.0000, 0.0000, 0.0000, 1.0000, 0.0000, 0.0000, 0.0000, 1.0000],
[0.2375, 0.0000, 0.0000, 0.5502, 0.0000, 1.0000, 1.0000, 0.0000, 0.0000, 0.0000, 0.0000, 1.0000],
[0.3000, 0.1250, 0.3333, 0.5122, 0.0000, 1.0000, 0.0000, 0.0000, 1.0000, 0.0000, 0.0000, 1.0000],
[0.3250, 0.0000, 0.0000, 0.5502, 1.0000, 0.0000, 1.0000, 0.0000, 0.0000, 1.0000, 0.0000, 0.0000],
[0.4000, 0.0000, 0.0000, 0.3476, 1.0000, 0.0000, 0.0000, 0.0000, 1.0000, 0.0000, 1.0000, 0.0000]])When calculating the predictions, each row of t_indep is element-wise multiplied by coeffs and is summed together with .sum(axis=1).
# calculate predictions
# predictions = matrix multiplication of independent variable values and parameters
# each row
preds = (t_indep*coeffs).sum(axis=1)
preds.shapetorch.Size([891])preds[:10]tensor([ 0.1927, -0.6239, 0.0979, 0.2056, 0.0968, 0.0066, 0.1306, 0.3476, 0.1613, -0.6285])To visualize the preds calculation, I’ll do the first prediction (0.1927) manually:
# multiply coeffs by first row of t_indep and take the sum
(t_indep[0]*coeffs)tensor([-0.1273, 0.0173, 0.0000, -0.0765, -0.2632, -0.0000, 0.0000, 0.0000, 0.2799, -0.0000, 0.0000, 0.3625])(t_indep[0]*coeffs).sum()tensor(0.1927)loss = torch.abs(preds-t_dep).mean()
losstensor(0.5382)# collect calculations into functions
def calc_preds(coeffs, indeps): return (indeps*coeffs).sum(axis=1)
def calc_loss(coeffs, indeps, deps): return torch.abs(calc_preds(coeffs, indeps)-deps).mean()# get ready to calculate gradient
coeffs.requires_grad_()tensor([-0.4629, 0.1386, 0.2409, -0.2262, -0.2632, -0.3147, 0.4876, 0.3136, 0.2799, -0.4392, 0.2103, 0.3625], requires_grad=True)loss = calc_loss(coeffs, t_indep, t_dep)
losstensor(0.5382, grad_fn=<MeanBackward0>)loss.backward()coeffs.gradtensor([-0.0106, 0.0129, -0.0041, -0.0484, 0.2099, -0.2132, -0.1212, -0.0247, 0.1425, -0.1886, -0.0191, 0.2043])If we calculate loss again and calculate the gradients they will be added to the existing gradients:
loss = calc_loss(coeffs, t_indep, t_dep)
loss.backward()
coeffs.grad # notice how these are 2x the original gradientstensor([-0.0212, 0.0258, -0.0082, -0.0969, 0.4198, -0.4265, -0.2424, -0.0494, 0.2851, -0.3771, -0.0382, 0.4085])This is why we set gradients back to zero.
loss = calc_loss(coeffs, t_indep, t_dep)
loss.backward()
with torch.no_grad():
coeffs.sub_(coeffs.grad * 0.1)
coeffs.grad.zero_()
print(calc_loss(coeffs, t_indep, t_dep))tensor(0.4945)Our loss decreased after doing gradient descent.
Split data into training and validation sets
from fastai.data.transforms import RandomSplitter# RandomSplitter gives indexes of the corresponding training/validation split
RandomSplitter(seed=42)(df)((#713) [788,525,821,253,374,98,215,313,281,305...],
(#178) [303,778,531,385,134,476,691,443,386,128...])trn_split,val_split=RandomSplitter(seed=42)(df)len(trn_split), len(val_split)(713, 178)Using the training and validation indexes, create training and validation set independent and dependent variables:
trn_indep,val_indep = t_indep[trn_split], t_indep[val_split]
trn_dep,val_dep = t_dep[trn_split], t_dep[val_split]trn_indep.shape, trn_dep.shape(torch.Size([713, 12]), torch.Size([713]))val_indep.shape, val_dep.shape(torch.Size([178, 12]), torch.Size([178]))Put the stepping the parameters code into a function:
def update_coeffs(coeffs, lr):
coeffs.sub_(coeffs.grad * lr)
coeffs.grad.zero_()Create function to train model for one epoch:
def one_epoch(coeffs, lr):
loss = calc_loss(coeffs, trn_indep, trn_dep)
loss.backward()
with torch.no_grad(): update_coeffs(coeffs, lr)
print(f"{loss:.3f}", end="; ")Create a function to initialize parameters:
def init_coeffs(): return (torch.rand(n_coeff)-0.5).requires_grad_()Create function to train a model for a given number of epochs:
def train_model(epochs=30, lr=0.01):
torch.manual_seed(442)
coeffs = init_coeffs()
for i in range(epochs): one_epoch(coeffs, lr=lr)
return coeffsTrain model for 18 epochs:
coeffs = train_model(18, lr=0.2)0.536; 0.502; 0.477; 0.454; 0.431; 0.409; 0.388; 0.367; 0.349; 0.336; 0.330; 0.326; 0.329; 0.304; 0.314; 0.296; 0.300; 0.289; The loss consistently decreases each epoch.
def show_coeffs(): return dict(zip(indep_cols, coeffs.requires_grad_(False)))Positive coefficients indicate a positive correlation with survival, negative coefficients indicate negative correlation. For example, Sex_male coefficient is negative meaning that survival variable decreases if Sex_male is 1.
show_coeffs(){'Age': tensor(-0.2694),
'SibSp': tensor(0.0901),
'Parch': tensor(0.2359),
'LogFare': tensor(0.0280),
'Sex_male': tensor(-0.3990),
'Sex_female': tensor(0.2345),
'Pclass_1': tensor(0.7232),
'Pclass_2': tensor(0.4112),
'Pclass_3': tensor(0.3601),
'Embarked_C': tensor(0.0955),
'Embarked_Q': tensor(0.2395),
'Embarked_S': tensor(0.2122)}With coefficients, we can calculate predictions and therefore accuracy:
preds = calc_preds(coeffs, val_indep)preds[:10]tensor([ 0.8160, 0.1295, -0.0148, 0.1831, 0.1520, 0.1350, 0.7279, 0.7754, 0.3222, 0.6740])preds.shape # recall that we split the data into training and validation setstorch.Size([178])val_dep.bool()[:10]tensor([ True, False, False, False, False, False, True, True, False, True])(preds>0.5)[:10]tensor([ True, False, False, False, False, False, True, True, False, True])results = val_dep.bool()==(preds>0.5)
results[:10]tensor([True, True, True, True, True, True, True, True, True, True])Calculate accuracy:
results.float().mean()tensor(0.7865)Put accuracy calculation into a function:
def acc(coeffs): return (val_dep.bool()==(calc_preds(coeffs, val_indep)>0.5)).float().mean()
acc(coeffs)tensor(0.7865)View sigmoid function:
import sympyNotice how large positive values of x result in y values closer to 1 and large negative x values result in y closer to 0.
We update our prediction calculation function to incorporate sigmoid:
def calc_preds(coeffs, indeps): return torch.sigmoid((indeps*coeffs).sum(axis=1))coeffs = train_model(lr=100)0.510; 0.327; 0.294; 0.207; 0.201; 0.199; 0.198; 0.197; 0.196; 0.196; 0.196; 0.195; 0.195; 0.195; 0.195; 0.195; 0.195; 0.195; 0.194; 0.194; 0.194; 0.194; 0.194; 0.194; 0.194; 0.194; 0.194; 0.194; 0.194; 0.194; acc(coeffs)tensor(0.8258)Sex_male’s coefficient has significantly increased (negatively):
show_coeffs(){'Age': tensor(-1.5061),
'SibSp': tensor(-1.1575),
'Parch': tensor(-0.4267),
'LogFare': tensor(0.2543),
'Sex_male': tensor(-10.3320),
'Sex_female': tensor(8.4185),
'Pclass_1': tensor(3.8389),
'Pclass_2': tensor(2.1398),
'Pclass_3': tensor(-6.2331),
'Embarked_C': tensor(1.4771),
'Embarked_Q': tensor(2.1168),
'Embarked_S': tensor(-4.7958)}Predict test data set values:
tst_df = pd.read_csv(path/'test.csv')tst_df.isna().sum()PassengerId 0
Pclass 0
Name 0
Sex 0
Age 86
SibSp 0
Parch 0
Ticket 0
Fare 1
Cabin 327
Embarked 0
dtype: int64Replace missing Fare with 0:
tst_df['Fare'] = tst_df.Fare.fillna(0)Replace other missing values with training set modes:
tst_df.fillna(modes, inplace=True)Apply the same data transformations as training set:
tst_df['LogFare'] = np.log(tst_df['Fare']+1)
tst_df = pd.get_dummies(tst_df, columns=['Sex', 'Pclass', 'Embarked'])tst_indep = tensor(tst_df[indep_cols].values, dtype=torch.float)
tst_indep = tst_indep / valstst_indep[:10]tensor([[0.4313, 0.0000, 0.0000, 0.3490, 1.0000, 0.0000, 0.0000, 0.0000, 1.0000, 0.0000, 1.0000, 0.0000],
[0.5875, 0.1250, 0.0000, 0.3332, 0.0000, 1.0000, 0.0000, 0.0000, 1.0000, 0.0000, 0.0000, 1.0000],
[0.7750, 0.0000, 0.0000, 0.3796, 1.0000, 0.0000, 0.0000, 1.0000, 0.0000, 0.0000, 1.0000, 0.0000],
[0.3375, 0.0000, 0.0000, 0.3634, 1.0000, 0.0000, 0.0000, 0.0000, 1.0000, 0.0000, 0.0000, 1.0000],
[0.2750, 0.1250, 0.1667, 0.4145, 0.0000, 1.0000, 0.0000, 0.0000, 1.0000, 0.0000, 0.0000, 1.0000],
[0.1750, 0.0000, 0.0000, 0.3725, 1.0000, 0.0000, 0.0000, 0.0000, 1.0000, 0.0000, 0.0000, 1.0000],
[0.3750, 0.0000, 0.0000, 0.3453, 0.0000, 1.0000, 0.0000, 0.0000, 1.0000, 0.0000, 1.0000, 0.0000],
[0.3250, 0.1250, 0.1667, 0.5450, 1.0000, 0.0000, 0.0000, 1.0000, 0.0000, 0.0000, 0.0000, 1.0000],
[0.2250, 0.0000, 0.0000, 0.3377, 0.0000, 1.0000, 0.0000, 0.0000, 1.0000, 1.0000, 0.0000, 0.0000],
[0.2625, 0.2500, 0.0000, 0.5167, 1.0000, 0.0000, 0.0000, 0.0000, 1.0000, 0.0000, 0.0000, 1.0000]])tst_indep.shapetorch.Size([418, 12])Calculate predictions in the format expected by Kaggle:
tst_df['Survived'] = (calc_preds(tst_indep, coeffs)>0.5).int()sub_df = tst_df[['PassengerId', 'Survived']]
sub_df.head()| PassengerId | Survived | |
|---|---|---|
| 0 | 892 | 0 |
| 1 | 893 | 0 |
| 2 | 894 | 0 |
| 3 | 895 | 0 |
| 4 | 896 | 0 |
Use @ operator for matrix multiplication:
(val_indep*coeffs).sum(axis=1)tensor([ 12.3288, -14.8119, -15.4540, -13.1513, -13.3512, -13.6469, 3.6248, 5.3429, -22.0878, 3.1233, -21.8742, -15.6421, -21.5504,
3.9393, -21.9190, -12.0010, -12.3775, 5.3550, -13.5880, -3.1015, -21.7237, -12.2081, 12.9767, 4.7427, -21.6525, -14.9135,
-2.7433, -12.3210, -21.5886, 3.9387, 5.3890, -3.6196, -21.6296, -21.8454, 12.2159, -3.2275, -12.0289, 13.4560, -21.7230,
-3.1366, -13.2462, -21.7230, -13.6831, 13.3092, -21.6477, -3.5868, -21.6854, -21.8316, -14.8158, -2.9386, -5.3103, -22.2384,
-22.1097, -21.7466, -13.3780, -13.4909, -14.8119, -22.0690, -21.6666, -21.7818, -5.4439, -21.7407, -12.6551, -21.6671, 4.9238,
-11.5777, -13.3323, -21.9638, -15.3030, 5.0243, -21.7614, 3.1820, -13.4721, -21.7170, -11.6066, -21.5737, -21.7230, -11.9652,
-13.2382, -13.7599, -13.2170, 13.1347, -21.7049, -21.7268, 4.9207, -7.3198, -5.3081, 7.1065, 11.4948, -13.3135, -21.8723,
-21.7230, 13.3603, -15.5670, 3.4105, -7.2857, -13.7197, 3.6909, 3.9763, -14.7227, -21.8268, 3.9387, -21.8743, -21.8367,
-11.8518, -13.6712, -21.8299, 4.9440, -5.4471, -21.9666, 5.1333, -3.2187, -11.6008, 13.7920, -21.7230, 12.6369, -3.7268,
-14.8119, -22.0637, 12.9468, -22.1610, -6.1827, -14.8119, -3.2838, -15.4540, -11.6950, -2.9926, -3.0110, -21.5664, -13.8268,
7.3426, -21.8418, 5.0744, 5.2582, 13.3415, -21.6289, -13.9898, -21.8112, -7.3316, 5.2296, -13.4453, 12.7891, -22.1235,
-14.9625, -3.4339, 6.3089, -21.9839, 3.1968, 7.2400, 2.8558, -3.1187, 3.7965, 5.4667, -15.1101, -15.0597, -22.9391,
-21.7230, -3.0346, -13.5206, -21.7011, 13.4425, -7.2690, -21.8335, -12.0582, 13.0489, 6.7993, 5.2160, 5.0794, -12.6957,
-12.1838, -3.0873, -21.6070, 7.0744, -21.7170, -22.1001, 6.8159, -11.6002, -21.6310])val_indep@coeffstensor([ 12.3288, -14.8119, -15.4540, -13.1513, -13.3511, -13.6468, 3.6248, 5.3429, -22.0878, 3.1233, -21.8742, -15.6421, -21.5504,
3.9393, -21.9190, -12.0010, -12.3775, 5.3550, -13.5880, -3.1015, -21.7237, -12.2081, 12.9767, 4.7427, -21.6525, -14.9135,
-2.7433, -12.3210, -21.5886, 3.9387, 5.3890, -3.6196, -21.6296, -21.8454, 12.2159, -3.2275, -12.0289, 13.4560, -21.7230,
-3.1366, -13.2462, -21.7230, -13.6831, 13.3092, -21.6477, -3.5868, -21.6854, -21.8316, -14.8158, -2.9386, -5.3103, -22.2384,
-22.1097, -21.7466, -13.3780, -13.4909, -14.8119, -22.0690, -21.6666, -21.7818, -5.4439, -21.7407, -12.6551, -21.6671, 4.9238,
-11.5777, -13.3323, -21.9638, -15.3030, 5.0243, -21.7614, 3.1820, -13.4721, -21.7170, -11.6066, -21.5737, -21.7230, -11.9652,
-13.2382, -13.7599, -13.2170, 13.1347, -21.7049, -21.7268, 4.9207, -7.3198, -5.3081, 7.1065, 11.4948, -13.3135, -21.8723,
-21.7230, 13.3603, -15.5670, 3.4105, -7.2857, -13.7197, 3.6909, 3.9763, -14.7227, -21.8268, 3.9387, -21.8743, -21.8367,
-11.8518, -13.6712, -21.8299, 4.9440, -5.4471, -21.9666, 5.1333, -3.2187, -11.6008, 13.7920, -21.7230, 12.6369, -3.7268,
-14.8119, -22.0637, 12.9468, -22.1610, -6.1827, -14.8119, -3.2838, -15.4540, -11.6950, -2.9926, -3.0110, -21.5664, -13.8268,
7.3426, -21.8418, 5.0744, 5.2582, 13.3415, -21.6289, -13.9898, -21.8112, -7.3316, 5.2296, -13.4453, 12.7891, -22.1235,
-14.9625, -3.4339, 6.3089, -21.9839, 3.1968, 7.2400, 2.8558, -3.1187, 3.7965, 5.4667, -15.1101, -15.0597, -22.9391,
-21.7230, -3.0346, -13.5206, -21.7011, 13.4425, -7.2690, -21.8335, -12.0582, 13.0489, 6.7993, 5.2160, 5.0794, -12.6957,
-12.1838, -3.0873, -21.6070, 7.0744, -21.7170, -22.1001, 6.8159, -11.6002, -21.6310])Update prediction calculation so that it uses matrix multiplication operator:
def calc_preds(coeffs, indeps): return torch.sigmoid(indeps@coeffs)Recreate coefficients and dependent variable so they are in the correct shape for matrix multiplication (when doing matrix-matrix products later on):
def init_coeffs(): return (torch.rand(n_coeff, 1)*0.1).requires_grad_()trn_dep.shape, val_dep.shape(torch.Size([713]), torch.Size([178]))trn_dep = trn_dep[:, None]
val_dep = val_dep[:, None]trn_dep.shape, val_dep.shape(torch.Size([713, 1]), torch.Size([178, 1]))coeffs = train_model(lr=100)0.512; 0.323; 0.290; 0.205; 0.200; 0.198; 0.197; 0.197; 0.196; 0.196; 0.196; 0.195; 0.195; 0.195; 0.195; 0.195; 0.195; 0.194; 0.194; 0.194; 0.194; 0.194; 0.194; 0.194; 0.194; 0.194; 0.194; 0.194; 0.194; 0.194; acc(coeffs)tensor(0.8258)Our model hasn’t changed other than the fact that we are now using matrix product explicitly.
Let’s create a neural net:
torch.rand(1)[0]tensor(0.6722)def init_coeffs(n_hidden=20):
layer1 = (torch.rand(n_coeff, n_hidden)-0.5)/n_hidden
layer2 = torch.rand(n_hidden, 1)-0.3
const = torch.rand(1)[0]
return layer1.requires_grad_(), layer2.requires_grad_(), const.requires_grad_()import torch.nn.functional as F
def calc_preds(coeffs, indeps):
l1, l2, const = coeffs
res = F.relu(indeps@l1)
res = res@l2 + const
return torch.sigmoid(res)As an aside, showing that the order of matrix multiplication operands matters—you get very different results:
tensor([[1,2,3], [4,5,6]]).shapetorch.Size([2, 3])tensor([[1, 2], [3, 4], [5, 6]]).shapetorch.Size([3, 2])tensor([[1,2,3], [4,5,6]]) @ tensor([[1, 2], [3, 4], [5, 6]])tensor([[22, 28],
[49, 64]])tensor([[1, 2], [3, 4], [5, 6]]) @ tensor([[1,2,3], [4,5,6]])tensor([[ 9, 12, 15],
[19, 26, 33],
[29, 40, 51]])Back to updating our functions to handle neural nets:
def update_coeffs(coeffs, lr):
for layer in coeffs:
layer.sub_(layer.grad * lr)
layer.grad.zero_()coeffs = train_model(lr=1.4)0.543; 0.532; 0.520; 0.505; 0.487; 0.466; 0.439; 0.407; 0.373; 0.343; 0.319; 0.301; 0.286; 0.274; 0.264; 0.256; 0.250; 0.245; 0.240; 0.237; 0.234; 0.231; 0.229; 0.227; 0.226; 0.224; 0.223; 0.222; 0.221; 0.220; coeffs = train_model(lr=20)0.543; 0.400; 0.260; 0.390; 0.221; 0.211; 0.197; 0.195; 0.193; 0.193; 0.193; 0.193; 0.193; 0.193; 0.193; 0.193; 0.193; 0.192; 0.192; 0.192; 0.192; 0.192; 0.192; 0.192; 0.192; 0.192; 0.192; 0.192; 0.192; 0.192; acc(coeffs)tensor(0.8258)Next we train a deep learning model:
def init_coeffs():
hiddens = [10,10]
sizes = [n_coeff] + hiddens + [1]
n = len(sizes)
layers = [(torch.rand(sizes[i], sizes[i+1])-0.3)/sizes[i+1]*4 for i in range(n-1)]
consts = [(torch.rand(1)[0]-0.5)*0.1 for i in range(n-1)]
for l in layers+consts: l.requires_grad_()
return layers,constsI’ll run through this function’s code line by line to make sure I see what’s going on:
hiddens = [10,10]sizes = [n_coeff] + hiddens + [1]
sizes[12, 10, 10, 1]n = len(sizes)
n4[(sizes[i], sizes[i+1]) for i in range (n-1)][(12, 10), (10, 10), (10, 1)][(torch.rand(1)[0]-0.5)*0.1 for i in range(n-1)][tensor(-0.0371), tensor(0.0406), tensor(-0.0461)]Cool! I can see it now. Next we update the function which calculates predictions to handle a deep neural net:
def calc_preds(coeffs, indeps):
layers,consts = coeffs
n = len(layers)
res = indeps
for i,l in enumerate(layers):
res = res@l + consts[i]
# pass through ReLU for all layers except the last one
if i!=n-1: res = F.relu(res)
return torch.sigmoid(res)def update_coeffs(coeffs, lr):
layers,consts = coeffs
for layer in layers+consts:
layer.sub_(layer.grad * lr)
layer.grad.zero_()coeffs = train_model(lr=4)0.521; 0.483; 0.427; 0.379; 0.379; 0.379; 0.379; 0.378; 0.378; 0.378; 0.378; 0.378; 0.378; 0.378; 0.378; 0.378; 0.377; 0.376; 0.371; 0.333; 0.239; 0.224; 0.208; 0.204; 0.203; 0.203; 0.207; 0.197; 0.196; 0.195; acc(coeffs)tensor(0.8258)That’s a wrap for that notebook! It all makes clear sense now after running through the code line by line. We trained a linear model, neural net, and deep learning model and got similar results. In this case, as discussed in the video, the deep learning model doesn’t improve our results.
Notebook Exercise: Why you should use a framework
In this section I run through the “clean” version of Jeremy’s notebook.
from fastai.tabular.all import *pd.options.display.float_format = '{:.2f}'.format
set_seed(42)# read in the data
df = pd.read_csv(path/'train.csv')# view the data
df.head()| PassengerId | Survived | Pclass | Name | Sex | Age | SibSp | Parch | Ticket | Fare | Cabin | Embarked | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 1 | 0 | 3 | Braund, Mr. Owen Harris | male | 22.00 | 1 | 0 | A/5 21171 | 7.25 | NaN | S |
| 1 | 2 | 1 | 1 | Cumings, Mrs. John Bradley (Florence Briggs Thayer) | female | 38.00 | 1 | 0 | PC 17599 | 71.28 | C85 | C |
| 2 | 3 | 1 | 3 | Heikkinen, Miss. Laina | female | 26.00 | 0 | 0 | STON/O2. 3101282 | 7.92 | NaN | S |
| 3 | 4 | 1 | 1 | Futrelle, Mrs. Jacques Heath (Lily May Peel) | female | 35.00 | 1 | 0 | 113803 | 53.10 | C123 | S |
| 4 | 5 | 0 | 3 | Allen, Mr. William Henry | male | 35.00 | 0 | 0 | 373450 | 8.05 | NaN | S |
# feature engineering
def add_features(df):
df['LogFare'] = np.log1p(df['Fare'])
df['Deck'] = df.Cabin.str[0].map(dict(A="ABC", B="ABC", C="ABC", D="DE", E="DE", F="FG", G="FG"))
df['Family'] = df.SibSp+df.Parch
df['Alone'] = df.Family == 0
df['TicketFreq'] = df.groupby('Ticket')['Ticket'].transform('count')
df['Title'] = df.Name.str.split(', ', expand=True)[1].str.split('.', expand=True)[0]
df['Title'] = df.Title.map(dict(Mr="Mr", Miss="Miss", Mrs="Mrs", Master="Master"))I’ll look at some of these in more detail to breakdown what is happening:
df.Cabin.str[0].unique()array([nan, 'C', 'E', 'G', 'D', 'A', 'B', 'F', 'T'], dtype=object)df.Cabin.str[0].map(dict(A="ABC", B="ABC", C="ABC", D="DE", E="DE", F="FG", G="FG")).unique()array([nan, 'ABC', 'DE', 'FG'], dtype=object)df.Ticket0 A/5 21171
1 PC 17599
2 STON/O2. 3101282
3 113803
4 373450
...
886 211536
887 112053
888 W./C. 6607
889 111369
890 370376
Name: Ticket, Length: 891, dtype: objectdf.groupby('Ticket')['Ticket'].transform('count')0 1
1 1
2 1
3 2
4 1
..
886 1
887 1
888 2
889 1
890 1
Name: Ticket, Length: 891, dtype: int64# there should be 2 count of this ticket
df.query('Ticket == "113803"')| PassengerId | Survived | Pclass | Name | Sex | Age | SibSp | Parch | Ticket | Fare | Cabin | Embarked | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 3 | 4 | 1 | 1 | Futrelle, Mrs. Jacques Heath (Lily May Peel) | female | 35.00 | 1 | 0 | 113803 | 53.10 | C123 | S |
| 137 | 138 | 0 | 1 | Futrelle, Mr. Jacques Heath | male | 37.00 | 1 | 0 | 113803 | 53.10 | C123 | S |
# expand = True splits into separate columns
df.Name.str.split(', ', expand=True).head()| 0 | 1 | |
|---|---|---|
| 0 | Braund | Mr. Owen Harris |
| 1 | Cumings | Mrs. John Bradley (Florence Briggs Thayer) |
| 2 | Heikkinen | Miss. Laina |
| 3 | Futrelle | Mrs. Jacques Heath (Lily May Peel) |
| 4 | Allen | Mr. William Henry |
df.Name.str.split(', ', expand=False)0 [Braund, Mr. Owen Harris]
1 [Cumings, Mrs. John Bradley (Florence Briggs Thayer)]
2 [Heikkinen, Miss. Laina]
3 [Futrelle, Mrs. Jacques Heath (Lily May Peel)]
4 [Allen, Mr. William Henry]
...
886 [Montvila, Rev. Juozas]
887 [Graham, Miss. Margaret Edith]
888 [Johnston, Miss. Catherine Helen "Carrie"]
889 [Behr, Mr. Karl Howell]
890 [Dooley, Mr. Patrick]
Name: Name, Length: 891, dtype: objectdf.Name.str.split(', ', expand=True)[1].str.split('.', expand=True)[0].unique()array(['Mr', 'Mrs', 'Miss', 'Master', 'Don', 'Rev', 'Dr', 'Mme', 'Ms',
'Major', 'Lady', 'Sir', 'Mlle', 'Col', 'Capt', 'the Countess',
'Jonkheer'], dtype=object)The line df.Title.map(dict(Mr="Mr", Miss="Miss", Mrs="Mrs", Master="Master")) reduces the number of titles to 4.
df.Name.str.split(', ', expand=True)[1].str.split('.', expand=True)[0].map(dict(Mr="Mr", Miss="Miss", Mrs="Mrs", Master="Master")).unique()array(['Mr', 'Mrs', 'Miss', 'Master', nan], dtype=object)# add the features to our dataframe
add_features(df)df.Title.unique()array(['Mr', 'Mrs', 'Miss', 'Master', nan], dtype=object)df.Deck.unique()array([nan, 'ABC', 'DE', 'FG'], dtype=object)df.Family.unique()array([ 1, 0, 4, 2, 6, 5, 3, 7, 10])df.Alone.unique()array([False, True])# create training and validation index lists
splits = RandomSplitter(seed=42)(df)splits((#713) [788,525,821,253,374,98,215,313,281,305...],
(#178) [303,778,531,385,134,476,691,443,386,128...])df.columnsIndex(['PassengerId', 'Survived', 'Pclass', 'Name', 'Sex', 'Age', 'SibSp',
'Parch', 'Ticket', 'Fare', 'Cabin', 'Embarked', 'LogFare', 'Deck',
'Family', 'Alone', 'TicketFreq', 'Title'],
dtype='object')# create dataloaders object
dls = TabularPandas(
df,
splits=splits,
procs=[Categorify, FillMissing, Normalize],
cat_names=["Sex", "Pclass", "Embarked", "Deck", "Title"],
cont_names=["Age", "SibSp", "Parch", "LogFare", "Alone", "TicketFreq", "Family"],
y_names="Survived",
y_block=CategoryBlock()
).dataloaders(path=".")# view a batch
dls.show_batch()| Sex | Pclass | Embarked | Deck | Title | Age_na | Age | SibSp | Parch | LogFare | Alone | TicketFreq | Family | Survived | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | male | 3 | Q | #na# | Mr | True | 28.00 | 1.00 | -0.00 | 2.80 | 0.00 | 2.00 | 1.00 | 0 |
| 1 | male | 3 | C | #na# | Mr | False | 30.00 | 0.00 | -0.00 | 2.11 | 1.00 | 1.00 | -0.00 | 0 |
| 2 | male | 3 | S | #na# | Mr | False | 28.00 | 2.00 | -0.00 | 2.19 | 0.00 | 1.00 | 2.00 | 0 |
| 3 | female | 3 | S | #na# | Miss | False | 45.00 | 0.00 | -0.00 | 2.17 | 1.00 | 1.00 | -0.00 | 0 |
| 4 | male | 2 | S | #na# | Mr | True | 28.00 | 0.00 | -0.00 | 0.00 | 1.00 | 1.00 | -0.00 | 0 |
| 5 | male | 3 | S | #na# | Mr | True | 28.00 | 0.00 | -0.00 | 2.78 | 1.00 | 1.00 | -0.00 | 0 |
| 6 | male | 1 | S | ABC | Mr | False | 38.00 | 0.00 | 1.00 | 5.04 | 0.00 | 3.00 | 1.00 | 0 |
| 7 | male | 1 | C | ABC | #na# | False | 32.00 | 0.00 | -0.00 | 3.45 | 1.00 | 1.00 | -0.00 | 1 |
| 8 | male | 2 | S | #na# | Mr | False | 24.00 | 2.00 | -0.00 | 4.31 | 0.00 | 5.00 | 2.00 | 0 |
| 9 | male | 2 | S | #na# | Mr | False | 48.00 | 0.00 | -0.00 | 2.64 | 1.00 | 1.00 | -0.00 | 0 |
learn = tabular_learner(dls, metrics=accuracy, layers=[10,10])learn.lr_find(suggest_funcs=(slide, valley))SuggestedLRs(slide=0.04786301031708717, valley=0.015848932787775993)learn.fit(16, lr=0.03)| epoch | train_loss | valid_loss | accuracy | time |
|---|---|---|---|---|
| 0 | 0.551385 | 0.558225 | 0.595506 | 00:00 |
| 1 | 0.498181 | 0.578588 | 0.752809 | 00:00 |
| 2 | 0.472778 | 0.471495 | 0.803371 | 00:00 |
| 3 | 0.447318 | 0.430369 | 0.825843 | 00:00 |
| 4 | 0.432644 | 0.454893 | 0.808989 | 00:00 |
| 5 | 0.421892 | 0.397669 | 0.825843 | 00:00 |
| 6 | 0.413710 | 0.406790 | 0.814607 | 00:00 |
| 7 | 0.406777 | 0.430182 | 0.825843 | 00:00 |
| 8 | 0.402777 | 0.434063 | 0.837079 | 00:00 |
| 9 | 0.397782 | 0.425264 | 0.814607 | 00:00 |
| 10 | 0.392991 | 0.413648 | 0.837079 | 00:00 |
| 11 | 0.390115 | 0.422005 | 0.820225 | 00:00 |
| 12 | 0.385480 | 0.412861 | 0.837079 | 00:00 |
| 13 | 0.383542 | 0.403564 | 0.820225 | 00:00 |
| 14 | 0.380573 | 0.422910 | 0.831461 | 00:00 |
| 15 | 0.378466 | 0.444065 | 0.820225 | 00:00 |
# prep test data for submission
tst_df = pd.read_csv(path/'test.csv')
tst_df['Fare'] = tst_df.Fare.fillna(0)
tst_df.columnsIndex(['PassengerId', 'Pclass', 'Name', 'Sex', 'Age', 'SibSp', 'Parch',
'Ticket', 'Fare', 'Cabin', 'Embarked'],
dtype='object')add_features(tst_df)
tst_df.columnsIndex(['PassengerId', 'Pclass', 'Name', 'Sex', 'Age', 'SibSp', 'Parch',
'Ticket', 'Fare', 'Cabin', 'Embarked', 'LogFare', 'Deck', 'Family',
'Alone', 'TicketFreq', 'Title'],
dtype='object')tst_dl = learn.dls.test_dl(tst_df)
tst_dl.show_batch()| Sex | Pclass | Embarked | Deck | Title | Age_na | Age | SibSp | Parch | LogFare | Alone | TicketFreq | Family | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | male | 3 | Q | #na# | Mr | False | 34.50 | 0.00 | -0.00 | 2.18 | 1.00 | 1.00 | -0.00 |
| 1 | female | 3 | S | #na# | Mrs | False | 47.00 | 1.00 | -0.00 | 2.08 | 0.00 | 1.00 | 1.00 |
| 2 | male | 2 | Q | #na# | Mr | False | 62.00 | 0.00 | -0.00 | 2.37 | 1.00 | 1.00 | -0.00 |
| 3 | male | 3 | S | #na# | Mr | False | 27.00 | 0.00 | -0.00 | 2.27 | 1.00 | 1.00 | -0.00 |
| 4 | female | 3 | S | #na# | Mrs | False | 22.00 | 1.00 | 1.00 | 2.59 | 0.00 | 1.00 | 2.00 |
| 5 | male | 3 | S | #na# | Mr | False | 14.00 | 0.00 | -0.00 | 2.32 | 1.00 | 1.00 | -0.00 |
| 6 | female | 3 | Q | #na# | Miss | False | 30.00 | 0.00 | -0.00 | 2.16 | 1.00 | 1.00 | -0.00 |
| 7 | male | 2 | S | #na# | Mr | False | 26.00 | 1.00 | 1.00 | 3.40 | 0.00 | 1.00 | 2.00 |
| 8 | female | 3 | C | #na# | Mrs | False | 18.00 | 0.00 | -0.00 | 2.11 | 1.00 | 1.00 | -0.00 |
| 9 | male | 3 | S | #na# | Mr | False | 21.00 | 2.00 | -0.00 | 3.22 | 0.00 | 1.00 | 2.00 |
get_preds returns predictions for both categories of Survived (0 and 1).
learn.get_preds(dl=tst_dl)[0][:5]tensor([[0.9141, 0.0859],
[0.5954, 0.4046],
[0.9711, 0.0289],
[0.9268, 0.0732],
[0.4136, 0.5864]])learn.get_preds(dl=tst_dl)[0][:5].sum(axis=1)tensor([1., 1., 1., 1., 1.])# targets are empty---why?
learn.get_preds(dl=tst_dl)[1]preds,_ = learn.get_preds(dl=tst_dl)tst_df['Survived'] = (preds[:,1]>0.5).int()tst_df.Survived.unique()array([0, 1], dtype=int32)sub_df = tst_df[['PassengerId', 'Survived']]sub_df.head()| PassengerId | Survived | |
|---|---|---|
| 0 | 892 | 0 |
| 1 | 893 | 0 |
| 2 | 894 | 0 |
| 3 | 895 | 0 |
| 4 | 896 | 1 |
# ensembling
def ensemble():
learn = tabular_learner(dls, metrics=accuracy, layers=[10,10])
with learn.no_bar(), learn.no_logging(): learn.fit(16, lr=0.03)
return learn.get_preds(dl=tst_dl)[0]learns = [ensemble() for _ in range(5)]ens_preds = torch.stack(learns).mean(0)torch.stack(learns).shapetorch.Size([5, 418, 2])ens_preds.shapetorch.Size([418, 2])tst_df['Survived'] = (ens_preds[:,1]>0.5).int()
sub_df = tst_df[['PassengerId', 'Survived']]sub_df.head()| PassengerId | Survived | |
|---|---|---|
| 0 | 892 | 0 |
| 1 | 893 | 0 |
| 2 | 894 | 0 |
| 3 | 895 | 0 |
| 4 | 896 | 1 |
Notebook Exercise: How random forests really work
In this section I run through the “clean” version of Jeremy’s notebook.
from fastai.imports import *
np.set_printoptions(linewidth=130)df = pd.read_csv(path/'train.csv')
tst_df = pd.read_csv(path/'test.csv')df.head()| PassengerId | Survived | Pclass | Name | Sex | Age | SibSp | Parch | Ticket | Fare | Cabin | Embarked | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 1 | 0 | 3 | Braund, Mr. Owen Harris | male | 22.00 | 1 | 0 | A/5 21171 | 7.25 | NaN | S |
| 1 | 2 | 1 | 1 | Cumings, Mrs. John Bradley (Florence Briggs Thayer) | female | 38.00 | 1 | 0 | PC 17599 | 71.28 | C85 | C |
| 2 | 3 | 1 | 3 | Heikkinen, Miss. Laina | female | 26.00 | 0 | 0 | STON/O2. 3101282 | 7.92 | NaN | S |
| 3 | 4 | 1 | 1 | Futrelle, Mrs. Jacques Heath (Lily May Peel) | female | 35.00 | 1 | 0 | 113803 | 53.10 | C123 | S |
| 4 | 5 | 0 | 3 | Allen, Mr. William Henry | male | 35.00 | 0 | 0 | 373450 | 8.05 | NaN | S |
tst_df.head()| PassengerId | Pclass | Name | Sex | Age | SibSp | Parch | Ticket | Fare | Cabin | Embarked | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 892 | 3 | Kelly, Mr. James | male | 34.50 | 0 | 0 | 330911 | 7.83 | NaN | Q |
| 1 | 893 | 3 | Wilkes, Mrs. James (Ellen Needs) | female | 47.00 | 1 | 0 | 363272 | 7.00 | NaN | S |
| 2 | 894 | 2 | Myles, Mr. Thomas Francis | male | 62.00 | 0 | 0 | 240276 | 9.69 | NaN | Q |
| 3 | 895 | 3 | Wirz, Mr. Albert | male | 27.00 | 0 | 0 | 315154 | 8.66 | NaN | S |
| 4 | 896 | 3 | Hirvonen, Mrs. Alexander (Helga E Lindqvist) | female | 22.00 | 1 | 1 | 3101298 | 12.29 | NaN | S |
modes = df.mode().iloc[0]
modesPassengerId 1
Survived 0.00
Pclass 3.00
Name Abbing, Mr. Anthony
Sex male
Age 24.00
SibSp 0.00
Parch 0.00
Ticket 1601
Fare 8.05
Cabin B96 B98
Embarked S
Name: 0, dtype: object# pre-processing
def proc_data(df):
df['Fare'] = df.Fare.fillna(0)
df.fillna(modes, inplace=True)
df['LogFare'] = np.log1p(df['Fare'])
df['Embarked'] = pd.Categorical(df.Embarked)
df['Sex'] = pd.Categorical(df.Sex)df.Embarked.unique()array(['S', 'C', 'Q', nan], dtype=object)pd.Categorical(df.Embarked).unique()['S', 'C', 'Q', NaN]
Categories (3, object): ['C', 'Q', 'S']proc_data(df)
proc_data(tst_df)df.columnsIndex(['PassengerId', 'Survived', 'Pclass', 'Name', 'Sex', 'Age', 'SibSp',
'Parch', 'Ticket', 'Fare', 'Cabin', 'Embarked', 'LogFare'],
dtype='object')tst_df.columnsIndex(['PassengerId', 'Pclass', 'Name', 'Sex', 'Age', 'SibSp', 'Parch',
'Ticket', 'Fare', 'Cabin', 'Embarked', 'LogFare'],
dtype='object')df.Sex0 male
1 female
2 female
3 female
4 male
...
886 male
887 female
888 female
889 male
890 male
Name: Sex, Length: 891, dtype: category
Categories (2, object): ['female', 'male']tst_df.Sex0 male
1 female
2 male
3 male
4 female
...
413 male
414 female
415 male
416 male
417 male
Name: Sex, Length: 418, dtype: category
Categories (2, object): ['female', 'male']cats=["Sex", "Embarked"]
conts=['Age', 'SibSp', 'Parch', 'LogFare', 'Pclass']
dep="Survived"Categoricals are stored as integers but shown as their labels:
df.Sex.head()0 male
1 female
2 female
3 female
4 male
Name: Sex, dtype: category
Categories (2, object): ['female', 'male']df.Sex.cat.codes.head()0 1
1 0
2 0
3 0
4 1
dtype: int8import seaborn as snsSex alone is a pretty good indicator of survival:
fig,axs = plt.subplots(1,2, figsize=(11,5))
sns.barplot(data=df, y=dep, x="Sex", ax=axs[0]).set(title="Survival rate")
sns.countplot(data=df, x="Sex", ax=axs[1]).set(title="Histogram");from numpy import random
from sklearn.model_selection import train_test_split
random.seed(42)
trn_df,val_df = train_test_split(df, test_size=0.25)
trn_df[cats] = trn_df[cats].apply(lambda x: x.cat.codes)
val_df[cats] = val_df[cats].apply(lambda x: x.cat.codes)trn_df[cats].head()| Sex | Embarked | |
|---|---|---|
| 298 | 1 | 2 |
| 884 | 1 | 2 |
| 247 | 0 | 2 |
| 478 | 1 | 2 |
| 305 | 1 | 2 |
val_df[cats].head()| Sex | Embarked | |
|---|---|---|
| 709 | 1 | 0 |
| 439 | 1 | 2 |
| 840 | 1 | 2 |
| 720 | 0 | 2 |
| 39 | 0 | 0 |
def xs_y(df):
xs = df[cats+conts].copy()
return xs,df[dep] if dep in df else Nonetrn_xs,trn_y = xs_y(trn_df)
val_xs,val_y = xs_y(val_df)trn_xs.head()| Sex | Embarked | Age | SibSp | Parch | LogFare | Pclass | |
|---|---|---|---|---|---|---|---|
| 298 | 1 | 2 | 24.00 | 0 | 0 | 3.45 | 1 |
| 884 | 1 | 2 | 25.00 | 0 | 0 | 2.09 | 3 |
| 247 | 0 | 2 | 24.00 | 0 | 2 | 2.74 | 2 |
| 478 | 1 | 2 | 22.00 | 0 | 0 | 2.14 | 3 |
| 305 | 1 | 2 | 0.92 | 1 | 2 | 5.03 | 1 |
trn_y.head()298 1
884 0
247 1
478 0
305 1
Name: Survived, dtype: int64# sex as the only predictor
preds = val_xs.Sex==0from sklearn.metrics import mean_absolute_error
mean_absolute_error(val_y, preds)0.21524663677130046df_fare = trn_df[trn_df.LogFare>0]
fig,axs = plt.subplots(1,2, figsize=(11,5))
sns.boxenplot(data=df_fare, x=dep, y="LogFare", ax=axs[0])
sns.kdeplot(data=df_fare, x="LogFare", ax=axs[1]);It looks like people survived for LogFare values above 2.7ish (2.5ish is the median LogFare value for deaths).
# LogFare as a sole predictor
preds = val_xs.LogFare>2.7mean_absolute_error(val_y, preds)0.336322869955157We get a larger error than Sex.
def _side_score(side, y):
tot = side.sum()
if tot<=1: return 0
return y[side].std()*totdef score(col, y, split):
lhs = col<=split
return (_side_score(lhs, y) + _side_score(~lhs, y))/len(y)score(trn_xs["Sex"], trn_y, 0.5)0.40787530982063946lhs = trn_xs["Sex"] <= 0.5lhs.sum()229trn_y[lhs].std()*lhs.sum()100.36927432272375trn_y[~lhs].std()*(~lhs).sum()172.0914326374634len(trn_y)668(100.36927432272375 + 172.0914326374634)/6680.40787530982063946score(trn_xs["LogFare"], trn_y, 2.7)0.47180873952099694A smaller score means less variation on each side.
def iscore(nm, split):
col = trn_xs[nm]
return score(col, trn_y, split)
from ipywidgets import interact
interact(nm=conts, split=15.5)(iscore);interact(nm=cats, split=15.5)(iscore);nm = "Age"
col = trn_xs[nm]
unq = col.unique()
unq.sort()
unqarray([ 0.42, 0.67, 0.75, 0.83, 0.92, 1. , 2. , 3. , 4. , 5. , 6. , 7. , 8. , 9. , 10. , 11. , 12. ,
13. , 14. , 14.5 , 15. , 16. , 17. , 18. , 19. , 20. , 21. , 22. , 23. , 24. , 24.5 , 25. , 26. , 27. ,
28. , 28.5 , 29. , 30. , 31. , 32. , 32.5 , 33. , 34. , 34.5 , 35. , 36. , 36.5 , 37. , 38. , 39. , 40. ,
40.5 , 41. , 42. , 43. , 44. , 45. , 45.5 , 46. , 47. , 48. , 49. , 50. , 51. , 52. , 53. , 54. , 55. ,
55.5 , 56. , 57. , 58. , 59. , 60. , 61. , 62. , 64. , 65. , 70. , 70.5 , 74. , 80. ])scores = np.array([score(col, trn_y, o) for o in unq if not np.isnan(o)])
unq[scores.argmin()]6.0scores.min()0.478316717508991score(trn_xs["Age"], trn_y, 6)0.478316717508991def min_col(df, nm):
col, y = df[nm], df[dep]
unq = col.dropna().unique()
scores = np.array([score(col, y, o) for o in unq if not np.isnan(o)])
idx = scores.argmin()
return unq[idx],scores[idx]min_col(trn_df, "Age")(6.0, 0.478316717508991)cols = cats+conts
{o: min_col(trn_df, o) for o in cols}{'Sex': (0, 0.40787530982063946),
'Embarked': (0, 0.47883342573147836),
'Age': (6.0, 0.478316717508991),
'SibSp': (4, 0.4783740258817434),
'Parch': (0, 0.4805296527841601),
'LogFare': (2.4390808375825834, 0.4620823937736597),
'Pclass': (2, 0.46048261885806596)}cols.remove("Sex")
ismale = trn_df.Sex==1
males, females = trn_df[ismale], trn_df[~ismale]{o: min_col(males, o) for o in cols}{'Embarked': (0, 0.3875581870410906),
'Age': (6.0, 0.3739828371010595),
'SibSp': (4, 0.3875864227586273),
'Parch': (0, 0.3874704821461959),
'LogFare': (2.803360380906535, 0.3804856231758151),
'Pclass': (1, 0.38155442004360934)}{o: min_col(females, o) for o in cols}{'Embarked': (0, 0.4295252982857327),
'Age': (50.0, 0.4225927658431649),
'SibSp': (4, 0.42319212059713535),
'Parch': (3, 0.4193314500446158),
'LogFare': (4.256321678298823, 0.41350598332911376),
'Pclass': (2, 0.3335388911567601)}The next split after Sex is Age<=6 for males and Pclass<=2 for females.
from sklearn.tree import DecisionTreeClassifier, export_graphviz
m = DecisionTreeClassifier(max_leaf_nodes=4).fit(trn_xs, trn_y);import graphvizdef draw_tree(t, df, size=10, ratio=0.6, precision=2, **kwargs):
s=export_graphviz(t, out_file=None, feature_names=df.columns, filled=True, rounded=True,
special_characters=True, rotate=False, precision=precision, **kwargs)
return graphviz.Source(re.sub('Tree {', f'Tree {{ size={size}; ratio={ratio}', s))def gini(cond):
act = df.loc[cond, dep]
return 1 - act.mean()**2 - (1-act).mean()**2gini(df.Sex=='female'), gini(df.Sex=='male')(0.3828350034484158, 0.3064437162277842)mean_absolute_error(val_y, m.predict(val_xs))0.2242152466367713mean_absolute_error(val_y, m.predict(val_xs))0.18385650224215247tst_df[cats] = tst_df[cats].apply(lambda x: x.cat.codes)
tst_xs, _ = xs_y(tst_df)tst_xs.head()| Sex | Embarked | Age | SibSp | Parch | LogFare | Pclass | |
|---|---|---|---|---|---|---|---|
| 0 | 1 | 1 | 34.50 | 0 | 0 | 2.18 | 3 |
| 1 | 0 | 2 | 47.00 | 1 | 0 | 2.08 | 3 |
| 2 | 1 | 1 | 62.00 | 0 | 0 | 2.37 | 2 |
| 3 | 1 | 2 | 27.00 | 0 | 0 | 2.27 | 3 |
| 4 | 0 | 2 | 22.00 | 1 | 1 | 2.59 | 3 |
def subm(preds, suff):
tst_df['Survived'] = preds
sub_df = tst_df[['PassengerId', 'Survived']]
sub_df.to_csv(f'sub-{suff}.csv', index=False)
subm(m.predict(tst_xs), 'tree')def get_tree(prop=0.75):
n = len(trn_y)
idxs = random.choice(n, int(n*prop))
return DecisionTreeClassifier(min_samples_leaf=5).fit(trn_xs.iloc[idxs], trn_y.iloc[idxs])trees = [get_tree() for t in range(100)]all_probs = [t.predict(val_xs) for t in trees]
avg_probs = np.stack(all_probs).mean(0)
mean_absolute_error(val_y, avg_probs)0.22811659192825115from sklearn.ensemble import RandomForestClassifierrf = RandomForestClassifier(100, min_samples_leaf=5)
rf.fit(trn_xs, trn_y);
mean_absolute_error(val_y, rf.predict(val_xs))0.18834080717488788Video Notes
- Kaggle sets an environment variable that you can check to see if you’re on Kaggle.
df.isna()returns aDataFramewith boolean values (Trueif the value isNaN).- If you call
sumon aDataFrameit sums up each column. - Easiest method to impute missing values is to replace them with the mode.
- Mode works for both categorical and continuous variables.
- First baseline model shouldn’t involve doing complicated things.
- Never throw out columns with missing values. Maybe it turns out that the row missing a value is great predictor.
- Some types of models (like linear) don’t like long-tailed distributions like
Fare. Neural nets are better behaved without them as well. - Things that grow exponentially you want to take the log of (money, population, etc.).
- Dummy variables turn categoricals into 1/0 valued columns for each categorical.
- For n levels if you create n 0/1 columns you don’t have to add a constant term to the model.
- You can create a 82% accurate model just using names.
- Idea of tensor came from notation in 1950. Ken Iverson.
- The most important attribute of a tensor is its
shape. The length of the shape is its rank.
Linear Model
- The number of coefficients we need is the number of columns in the independent variable.
- Computers can’t create truly random numbers and instead create a sequence of numbers that behave in a random-like way.
- A lot of people are into reproducible results—Jeremy disagrees. An important part of understanding your data is understanding how much it varies from run to run. Run things a few times and get an intuitive sense of how stable it is.
- broadcasting comes from APL. Happens in optimized C code (CPU) or CUDA (GPU). As long as the last axes match it’ll broadcast. It uses a kind of “virtual copying”.
- Linear model: coefficients times the values, added together.
Ageis bigger than any other columns so it will always have a larger value. Not ideal for optimization.- Normalize the columns (divide by maximum in the column).
- Another common way to normalize is subtracting the mean and dividing by the standard deviation.
- Mean absolute value is a good loss function to start with.
- In notebooks, do everything step-by-step manually and then copy it into a function.
- PyTorch functions with an underscore at the end will do an in-place operation.
.backward()calls the gradient function.- If the gradient is negative it means that if we increase that coefficient, the loss will go down. If it’s positive that means if we decrease that coefficient, the loss will go down.
RandomSplitter(seed=42)(df)returns indexes (training, validation) of the split.- We can’t use accuracy as a loss function because it doesn’t have a smooth gradient.
- Sigmoid makes it easier to optimize—optimizer doesn’t have to exactly hit 0 or 1, it can predict a really big number and it gets converted to 1 or a really small number that gets converted to 0.
- Sigmoid =
1/(1+exp(-x)) sympypackage does symbolic calculations and plots.- With sigmoid, we could increae the learning rate from
0.1to2, showing that it truly is easier to optimize. - binary dependent variable: chuck it through sigmoid.
- fastai always creates an extra category called “other” for categorical columns. At test time if you have a level that wasn’t in training, fastai puts it into the “other” category for you.
- For categorical variables fastai puts less common ones into “other”.
Neural Net Model
(indeps*coeffs).sum(axis=1)is the same thing as matrix multiplication.init_coeffschanged to create anncoeffby1matrix instead of anncoeffvector, since for the neural net we will have multiple columns of coefficients.tensor[:,None]indexes into second dimensionNoneit creates that dimension.- Dimension of
1is a “unit axis”. torch.Size([12, 1])represents a rank-2 tensor with a trailing unit axis.- If our coefficients are too big or too small, it’s not going to train at all so you have to fiddle with their magnitude in a from-scratch model.
Deep Learning Model
- Jeremy divides the first layer coefficients by
n_hiddensince the coeffs will get multiplied by a second layer as well and we want the coeffs to be a similar size as the linear model. - The final layer absolutely needs a constant term.
- A deep learning model has multiple hidden layers.
torch.sigmoidandF.reluare the activation functions for the layers.- For very small datasets with very few columns and columns that are really simple, deep learning is not necessarily going to give you the best result. Nothing is going to be as good as a carefully designed model that uses just the name column.
- For data types which have a very consitent structure like images or natural language text documents you can chuck a deep learning neural net at it and expect great results. Generally for tabular data that’s not the case. Normally have to think pretty long and hard about feature engineering to get good results.
- You want to make choices for the non-obvious things and have the obvious things done for you by a package like fastai.
Using fastai
Categorifyhandles dummy variables.learner.lr_findstarts at a very small learning rate like10e-7, trains one batch of data and calculates the loss, increases the learning rate slightly and calculates the loss again. Picking a learning rate betweenslideandvalleygenerally works well for training.learn.dls.test_dlcreates aDataLoaderthat contains exactly the same processing steps that our learner used.- You want to make sure your inference time pre-processing and transformations are exactly the same as training time.
- Ensembling is about creating multiple models and combining their predictions.
Random Forests
- Random forets are elegant, and almost impossible to mess up. Jeremy has seen far more examples in industry of people messing up logistic regression than random forests.
- Handy shortcut:
from fastai.imports import *. df.col_name.cat.codesshows actual values (numbers corresponding to list of categories) for categorical column.- A random forest is an ensemble of trees, a tree is an ensemble of binary splits.
- A binary split is something that splits the rows into two groups.
- Kernel density plot is like a histogram with infinitesimally narrow bins.
- A good split is one where all of the values of the dependent variable on one side are all pretty much the same and all of dependent variable values on the other side are pretty much the same.
- You want each of your groups, within the group, to be as similar as possible on the dependent variable.
- “how similar are all the things in the group” = standard deviation.
- Sex is the best single binary split model we can find.
- “OneR” model: create a single binary split and stop.
- Don’t assume that you have to go complicated. It’s not a bad idea of always creating a baseline of OneR (a decision tree with a single binary split).
Book Notes
- The objective of tabular modeling is to predict the value in one column based on the values in the other columns.
Categorical Embeddings
- Continuous variables can be directly fed to the model (with some optional preprocessing).
- Categorical variables need to be converted to numbers. Addition and multiplication don’t have meaning for them even if they’re stored as numbers.
- Rossmann competition example notebook
- The embedding layer is just another layer in the model.
- The embedding transforms the categorical variables into inputs that are both continuous and meaningful.
- The raw categorical data is transformed by an embedding layer before it interacts with the raw continuous input data.
- Deep learning is not always the best starting point fo analyzing tabular data.
Beyond Deep Learning
- Recent studies have shown that the vast majority of datasets can be best modeled with just two methods:
- Ensembles of decision trees (random forests and gradient boosting machines), mainly for structured data. They train faster, are often easier to interpret, do not require GPU for inference at scale, often require less hyperparameter tuning, and have a more mature ecosystem of tooling and documentation.
- Multilayered neural networks learned with SGD (shallow and/or deep learning) mainly for unstructured data (audio, images, and natural language)
- The critical step of interpreting a model of tabular data is significantly easier for decision tree ensembles.
- There are tools and methods for answering questions like:
- Which columns in the dataset were the most important for your predictions?
- How are they related to the dependent variable?
- How do they interact with each other?
- Which particular features were most important for some particular observation?
- Ensembles of decision trees are our first approach for analyzing a new tabular dataset except when there are some high-cardinality categorical variables that are very important or when there are some columns that contain data that would be understood with a neural network such as plain text data.
The Dataset
- Blue Book for Bulldozers Kaggle competition: the goal of the contest is to predict the sale price of a particular piece of heavy equipment at auction based on its usage, equipment type, and configuration.
!pip install dtreeviz
from pandas.api.types import is_string_dtype, is_numeric_dtype, is_categorical_dtype
from fastai.tabular.all import *
from sklearn.ensemble import RandomForestRegressor
from sklearn.tree import DecisionTreeRegressor
from dtreeviz.trees import *
from IPython.display import Image, display_svg, SVG
pd.options.display.max_rows = 20
pd.options.display.max_columns = 8from pathlib import Path
cred_path = Path("~/.kaggle/kaggle.json").expanduser()
if not cred_path.exists():
cred_path.parent.mkdir(exist_ok=True)
cred_path.write_text(creds)
cred_path.chmod(0o600)import zipfile,kaggle
path = Path('bluebook-for-bulldozers')
if not path.exists():
kaggle.api.competition_download_cli(str(path))
zipfile.ZipFile(f'{path}.zip').extractall(path)Downloading bluebook-for-bulldozers.zip to /content100%|██████████| 48.4M/48.4M [00:01<00:00, 36.3MB/s]path.ls(file_type='text')(#7) [Path('bluebook-for-bulldozers/Valid.csv'),Path('bluebook-for-bulldozers/median_benchmark.csv'),Path('bluebook-for-bulldozers/Test.csv'),Path('bluebook-for-bulldozers/Machine_Appendix.csv'),Path('bluebook-for-bulldozers/TrainAndValid.csv'),Path('bluebook-for-bulldozers/ValidSolution.csv'),Path('bluebook-for-bulldozers/random_forest_benchmark_test.csv')]df = pd.read_csv(path/'TrainAndValid.csv', low_memory=False)len(df.columns)53df.columnsIndex(['SalesID', 'SalePrice', 'MachineID', 'ModelID', 'datasource',
'auctioneerID', 'YearMade', 'MachineHoursCurrentMeter', 'UsageBand',
'saledate', 'fiModelDesc', 'fiBaseModel', 'fiSecondaryDesc',
'fiModelSeries', 'fiModelDescriptor', 'ProductSize',
'fiProductClassDesc', 'state', 'ProductGroup', 'ProductGroupDesc',
'Drive_System', 'Enclosure', 'Forks', 'Pad_Type', 'Ride_Control',
'Stick', 'Transmission', 'Turbocharged', 'Blade_Extension',
'Blade_Width', 'Enclosure_Type', 'Engine_Horsepower', 'Hydraulics',
'Pushblock', 'Ripper', 'Scarifier', 'Tip_Control', 'Tire_Size',
'Coupler', 'Coupler_System', 'Grouser_Tracks', 'Hydraulics_Flow',
'Track_Type', 'Undercarriage_Pad_Width', 'Stick_Length', 'Thumb',
'Pattern_Changer', 'Grouser_Type', 'Backhoe_Mounting', 'Blade_Type',
'Travel_Controls', 'Differential_Type', 'Steering_Controls'],
dtype='object')len(df.SalesID.unique())412698len(df.MachineID.unique())348808df.MachineHoursCurrentMeter.unique()array([ 68., 4640., 2838., ..., 11612., 12097., 14650.])df.Forks.unique()array(['None or Unspecified', nan, 'Yes'], dtype=object)df.Pad_Type.unique()array([nan, 'None or Unspecified', 'Reversible', 'Street', 'Grouser'],
dtype=object)df.Backhoe_Mounting.unique()array([nan, 'None or Unspecified', 'Yes'], dtype=object)df.ProductSize.unique()array([nan, 'Medium', 'Small', 'Large / Medium', 'Mini', 'Large',
'Compact'], dtype=object)df.SalePrice.unique()[:10]array([66000., 57000., 10000., 38500., 11000., 26500., 21000., 27000.,
21500., 65000.])Tell pandas about a suitable ordering of these levels like so:
sizes = 'Large', 'Large / Medium', 'Medium', 'Small', 'Mini', 'Compact'
df['ProductSize'] = df['ProductSize'].astype('category')
df['ProductSize'].cat.set_categories(sizes, ordered=True, inplace=True)FutureWarning: The `inplace` parameter in pandas.Categorical.set_categories is deprecated and will be removed in a future version. Removing unused categories will always return a new Categorical object.# I believe the ordering should be reverse of this
df.ProductSize.unique()[NaN, 'Medium', 'Small', 'Large / Medium', 'Mini', 'Large', 'Compact']
Categories (6, object): ['Large' < 'Large / Medium' < 'Medium' < 'Small' < 'Mini' < 'Compact']The metric we will use is RMLSE (root mean squared log error) between the actual and predicted auction prices. Take the log of the prices so that the m_rmse of that value will give us the metric.
dep_var = 'SalePrice'
df[dep_var] = np.log(df[dep_var])Decision Trees
A decision tree asks a series of binary (yes or no) questions about the data. After each question the data at that part of the tree is split between a Yes and a No branch. After one or more questions, either a prediction can be made on the basis of all previous answers or another question is required.
The basic steps to train a decision tree:
- Loop through each column of the dataset in turn.
- For each column, loop through each possible level of that column in turn.
- Try splitting the data into two groups, based on whether they are greater than or less than that value (or if it is a categorical variable, based on whether they are equal to or not equal to that level of that categorical variable).
- Find the average sale price for each of those two groups, and see how close that is to the actual sale price of each of the items of equipment in that group. Treat this as a very simple “model” in which our predictions are simply the average sale price of the item’s group.
- After looping through all of the columns and all the possible levels for each, pick the split point that gave the best predictions using that simple model.
- We now have two groups of our data, based on the selected split. Treat each group as a separate dataset, and find the best split for each by going back to step 1 for each group.
- Continue this process recursively until you have reached some stopping criterion for each group–for instance, stop splitting a group further when it has only 20 items in it.
Handling Dates
To help our algorithm handle dates intelligently, we’d like our model to know more than whether a date is more recent or less recent than another. We might want our model to make decisions based on that date’s day of the week, on whether a day is a holiday, on what month it is in, and so forth. To do this, replace every date column with a set of date metadata columns, such as holiday, day of week, and month. These columns provide categorical data that we suspect will be useful.
df = add_datepart(df, 'saledate')
df_test = pd.read_csv(path/'Test.csv', low_memory=False)
df_test = add_datepart(df_test, 'saledate')len(df.columns)65' '.join(o for o in df.columns if o.startswith('sale'))'saleYear saleMonth saleWeek saleDay saleDayofweek saleDayofyear saleIs_month_end saleIs_month_start saleIs_quarter_end saleIs_quarter_start saleIs_year_end saleIs_year_start saleElapsed'Using TabularPandas and TabularProc
A TabularProc is like a regular Transform except for the following:
- It returns the exact same object that’s passed to it, after modifying the object in place.
- It runs the transform once, when data is first passed in, rather than lazily as the data is accessed.
Categorify is a TabularProc that replaces a column with a numerical categorical column. FillMissing is a TabularProc that replaces missing values with the median of the column, and creates a new Boolean column that is set to True for any row where the value was missing.
procs = [Categorify, FillMissing]We need to be very careful about our validation set. We want to design it so that it is like the test set Kaggle will use to judge the contest.
The test set date range is from May 2012 to November 2012.
(df_test.saleYear.astype(str) + "/" + df_test.saleMonth.astype(str)).unique()array(['2012/5', '2012/6', '2012/7', '2012/8', '2012/9', '2012/10',
'2012/11'], dtype=object)The test set dates are later than any data in the training set (which has a latest date of April 2012).
np.sort((df.saleYear.astype(str) + "/" + df.saleMonth.astype(str)).unique())[-10:]array(['2011/4', '2011/5', '2011/6', '2011/7', '2011/8', '2011/9',
'2012/1', '2012/2', '2012/3', '2012/4'], dtype=object)We’ll define a validation set consisting of data from after November 2011.
cond = (df.saleYear<2011) | (df.saleMonth<10)
train_idx = np.where( cond)[0]
valid_idx = np.where(~cond)[0]
splits = (list(train_idx), list(valid_idx))TabularPandas needs to be told which columns are continuous and which are categorical.
cont,cat = cont_cat_split(df, 1, dep_var=dep_var)to = TabularPandas(df, procs, cat, cont, y_names=dep_var, splits=splits)len(to.train), len(to.valid)(404710, 7988)The data is still displayed as strings for categories.
to.show(3)| UsageBand | fiModelDesc | fiBaseModel | fiSecondaryDesc | fiModelSeries | fiModelDescriptor | ProductSize | fiProductClassDesc | state | ProductGroup | ProductGroupDesc | Drive_System | Enclosure | Forks | Pad_Type | Ride_Control | Stick | Transmission | Turbocharged | Blade_Extension | Blade_Width | Enclosure_Type | Engine_Horsepower | Hydraulics | Pushblock | Ripper | Scarifier | Tip_Control | Tire_Size | Coupler | Coupler_System | Grouser_Tracks | Hydraulics_Flow | Track_Type | Undercarriage_Pad_Width | Stick_Length | Thumb | Pattern_Changer | Grouser_Type | Backhoe_Mounting | Blade_Type | Travel_Controls | Differential_Type | Steering_Controls | saleIs_month_end | saleIs_month_start | saleIs_quarter_end | saleIs_quarter_start | saleIs_year_end | saleIs_year_start | auctioneerID_na | MachineHoursCurrentMeter_na | SalesID | MachineID | ModelID | datasource | auctioneerID | YearMade | MachineHoursCurrentMeter | saleYear | saleMonth | saleWeek | saleDay | saleDayofweek | saleDayofyear | saleElapsed | SalePrice | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | Low | 521D | 521 | D | #na# | #na# | #na# | Wheel Loader - 110.0 to 120.0 Horsepower | Alabama | WL | Wheel Loader | #na# | EROPS w AC | None or Unspecified | #na# | None or Unspecified | #na# | #na# | #na# | #na# | #na# | #na# | #na# | 2 Valve | #na# | #na# | #na# | #na# | None or Unspecified | None or Unspecified | #na# | #na# | #na# | #na# | #na# | #na# | #na# | #na# | #na# | #na# | #na# | #na# | Standard | Conventional | False | False | False | False | False | False | False | False | 1139246 | 999089 | 3157 | 121 | 3.0 | 2004 | 68.0 | 2006 | 11 | 46 | 16 | 3 | 320 | 1.163635e+09 | 11.097410 |
| 1 | Low | 950FII | 950 | F | II | #na# | Medium | Wheel Loader - 150.0 to 175.0 Horsepower | North Carolina | WL | Wheel Loader | #na# | EROPS w AC | None or Unspecified | #na# | None or Unspecified | #na# | #na# | #na# | #na# | #na# | #na# | #na# | 2 Valve | #na# | #na# | #na# | #na# | 23.5 | None or Unspecified | #na# | #na# | #na# | #na# | #na# | #na# | #na# | #na# | #na# | #na# | #na# | #na# | Standard | Conventional | False | False | False | False | False | False | False | False | 1139248 | 117657 | 77 | 121 | 3.0 | 1996 | 4640.0 | 2004 | 3 | 13 | 26 | 4 | 86 | 1.080259e+09 | 10.950807 |
| 2 | High | 226 | 226 | #na# | #na# | #na# | #na# | Skid Steer Loader - 1351.0 to 1601.0 Lb Operating Capacity | New York | SSL | Skid Steer Loaders | #na# | OROPS | None or Unspecified | #na# | #na# | #na# | #na# | #na# | #na# | #na# | #na# | #na# | Auxiliary | #na# | #na# | #na# | #na# | #na# | None or Unspecified | None or Unspecified | None or Unspecified | Standard | #na# | #na# | #na# | #na# | #na# | #na# | #na# | #na# | #na# | #na# | #na# | False | False | False | False | False | False | False | False | 1139249 | 434808 | 7009 | 121 | 3.0 | 2001 | 2838.0 | 2004 | 2 | 9 | 26 | 3 | 57 | 1.077754e+09 | 9.210340 |
Bu the underlying items are all numeric:
to.items[["state", "ProductGroup", "Drive_System", "Enclosure"]].head(3)| state | ProductGroup | Drive_System | Enclosure | |
|---|---|---|---|---|
| 0 | 1 | 6 | 0 | 3 |
| 1 | 33 | 6 | 0 | 3 |
| 2 | 32 | 3 | 0 | 6 |
There’s no particular meaning to the numbers in the categorical columns after conversion, they are chosen consecutively as they are seen in a column. The exception is if you first convert a column to a Pandas ordered category.
to.classes['ProductSize']['#na#', 'Large', 'Large / Medium', 'Medium', 'Small', 'Mini', 'Compact']Creating the Decision Tree
xs,y = to.train.xs, to.train.y
valid_xs, valid_y = to.valid.xs, to.valid.ym = DecisionTreeRegressor(max_leaf_nodes=4)
m.fit(xs,y);from sklearn.tree import DecisionTreeClassifier, export_graphviz
import graphviz
def draw_tree(t, df, size=10, ratio=0.6, precision=2, **kwargs):
s=export_graphviz(t, out_file=None, feature_names=df.columns, filled=True, rounded=True,
special_characters=True, rotate=False, precision=precision, **kwargs)
return graphviz.Source(re.sub('Tree {', f'Tree {{ size={size}; ratio={ratio}', s))The topmost node is the initial model when all data is in one group. Predicts the average value of the whole dataset. In this case it predicts 10.1 for the logarithm of the sales price, and gives a mean squared error of 0.48. The square root of this is 0.69. There are 404710 records in this group which is the total size of our training set. The best split found was a split based on the coupler_system columns. Asking only about coupler_system predicts an average value of 9.21 versus 10.1.
import dtreevizsamp_idx = np.random.permutation(len(y))[:500]
viz_model=dtreeviz.model(m,
X_train=xs.iloc[samp_idx],
y_train=y.iloc[samp_idx],
feature_names=xs.columns,
target_name=dep_var)
viz_model.view(fontname='DejaVu Sans', scale=1.6, label_fontsize=10,
orientation='LR')/usr/local/lib/python3.10/dist-packages/sklearn/base.py:439: UserWarning: X does not have valid feature names, but DecisionTreeRegressor was fitted with feature namesThe YearMade data has values of 1000 which we need to change to make it more realistic:
xs.loc[xs['YearMade']<1900, 'YearMade'] = 1950
valid_xs.loc[valid_xs['YearMade']<1900, 'YearMade'] = 1950m = DecisionTreeRegressor(max_leaf_nodes=4).fit(xs,y);viz_model=dtreeviz.model(m,
X_train=xs.iloc[samp_idx],
y_train=y.iloc[samp_idx],
feature_names=xs.columns,
target_name=dep_var)
viz_model.view(fontname='DejaVu Sans', scale=1.6, label_fontsize=10,
orientation='LR')/usr/local/lib/python3.10/dist-packages/sklearn/base.py:439: UserWarning: X does not have valid feature names, but DecisionTreeRegressor was fitted with feature namesThe change in YearMade doesn’t change the model in any significant way—shows how resilient decision trees are to data issues.
Build a bigger tree (don’t pass any stopping criteria).
m = DecisionTreeRegressor()
m.fit(xs,y);def r_mse(pred,y): return round(math.sqrt(((pred-y)**2).mean()), 6)
def m_rmse(m, xs, y): return r_mse(m.predict(xs), y)m_rmse(m, xs, y)0.0The model has 0.0 root mean square error but that is on the training set. Let’s check the validation error:
m_rmse(m, valid_xs, valid_y)0.331731The model is overfitting pretty badly.
m.get_n_leaves(), len(xs)(324567, 404710)We have nearly as many leaf nodes as data points.
Let’s change the stopping rule to tell sklearn to ensure every leaf node contains at least 25 auction records:
m = DecisionTreeRegressor(min_samples_leaf=25)
m.fit(to.train.xs, to.train.y)
m_rmse(m, xs, y), m_rmse(m, valid_xs, valid_y)(0.248564, 0.323369)That looks better.
m.get_n_leaves()12397Random Forests
- Leo Breiman in 1994 while retired published a technical report called “Bagging Predictors” which turned out to be one of the most influential ideas in modern machine learning.
- Here is his procedure, known as bagging:
- Randomly choose a subset of rows of your data.
- Train a model using this subset.
- Save that model, and then return to step 1 a few times.
- This will give you multiple trained models. To make a prediction, predict using all of the models, and then take the average of each of those model’s predictions.
- Although each of the models trained on a subset of data will make more errors than a model trained on the full dataset, those errors will not be correlated with each other. Different models will make different errors. The average of those errors is zero.
- If we take the average of all of the models’ predictions, we should end up with a prediction that gets closer and closer to the correct answer, the more models we have.
- We can improve the accuracy of nearly any kind of machine learning algorithm by training it multiple times, each time on a different random subset of data, and averaging its predictions.
- Random Forest: a model that averages the predictions of a large number of decision trees which are generated by randomly varying various parameters that specify what data is used to train the tree and other tree parameters.
- Ensembling: combining the results of multiple models together.
Creating a Random Forest
- Similar to creating a decision tree except now we are also specifying parameters that indicate how many trees should be in the forest, how we should subset the data items (the rows) and how we should subset the fields (the columns).
- In the function
rf:n_estimators: number of trees.max_samples: number of rows to sample for training each tree.max_features: how many columns to sample at each split point (where0.5means “take half the total number of columns).min_samples_leaf: when to stop splitting the tree nodes.n_jobs=-1: tell sklearn to use all our CPUs to buil the trees in parallel.
def rf(xs, y, n_estimators=40, max_samples=200_000, max_features=0.5, min_samples_leaf=5, **kwargs):
return RandomForestRegressor(n_jobs=-1, n_estimators=n_estimators, max_samples=max_samples, max_features=max_features, min_samples_leaf=min_samples_leaf, oob_score=True).fit(xs,y)m = rf(xs, y);m_rmse(m, xs, y), m_rmse(m, valid_xs, valid_y)(0.170922, 0.233145)Random forests aren’t very sensitive to the hyperparameter choices such as max_features. You can st n_estimators to as high a number as you have time to train. The more trees you have the more accuracte the model will be. If you have over 200k data points, set max_samples to 200k and it will train faster with little impact on accuracy. The models with the lowest error result from using a subset of features with a larger number of trees.
Get the predictions from each individual tree in our forest:
preds = np.stack([t.predict(valid_xs) for t in m.estimators_]);r_mse(preds.mean(0), valid_y)0.233145The improvement levels off quite a bit after around 30 trees.
We don’t know if the performance on the validation set is worse than on our training set because we’re overfitting or because the validation set covers a different time period.
Out-of-Bag Error
In a random forest, each tree is trained on a different subset of the training data. The OOB error is a way of measuring prediction error in the training dataset by including in the calculation of a row’s error trees only where that row was not included in training. This allows us to see whether the model is overfitting without needing a separate validation set. Since every tree was trained with a different randomly selected subset of rows, out-of-bag error is a little like imagining that every tree therefore also has its own validation set, which is simply the rows that were not selected for that tree’s training. This is particularly beneficial when you have a small amount of training data.
len(m.oob_prediction_)404710# use training y
r_mse(m.oob_prediction_, y)0.210661OOB error is lower than validation set error, which means that something else is causing that error, in addition to normal generalization error. I’m not sure what that means but the text says it’s looked into later in this chapter.
Model Interpretation
- How confident are we in our predictions using a particular row of data?
- For predicting with a particular row of data, what were the most important factors, and how did they influence that prediction?
- Which columns are the strongest predictors, which can we ignore?
- Which columns are effectively redundant with each other, for purposes of prediction?
- How do predictions vary as we vary these columns?
Tree Variance for Prediction Confidence
The standard deviation of predictions across the trees tells us the relative confidence of predictions. We would want to be more cautious of using the results for rows where trees give very different results (higher standard deviations), compared to cases where they are more consistent (lower standard deviations).
We have a prediction for every tree and every auction in the validation set (40 trees and 7,988 auctions):
preds = np.stack([t.predict(valid_xs) for t in m.estimators_]);preds.shape(40, 7988)Get the standard deviation of the predictions over all the trees for each auction:
preds_std = preds.std(0)
preds_std[:5]array([0.21168835, 0.09996709, 0.0911939 , 0.25939701, 0.08520345])len(preds_std)7988The confidence in the predictions varies widely. For some auctions there is low std meaning the trees agree. For others it’s higher, meaning the trees don’t agree.
Feature Importance
def rf_feat_importance(m, df):
return pd.DataFrame({
'cols': df.columns,
'imp': m.feature_importances_}
).sort_values('imp', ascending=False)fi = rf_feat_importance(m, xs)
fi[:10]| cols | imp | |
|---|---|---|
| 57 | YearMade | 0.180981 |
| 6 | ProductSize | 0.116321 |
| 30 | Coupler_System | 0.089648 |
| 7 | fiProductClassDesc | 0.074037 |
| 32 | Hydraulics_Flow | 0.064145 |
| 54 | ModelID | 0.059373 |
| 31 | Grouser_Tracks | 0.053432 |
| 65 | saleElapsed | 0.050231 |
| 3 | fiSecondaryDesc | 0.043258 |
| 1 | fiModelDesc | 0.031560 |
def plot_fi(fi):
return fi.plot('cols', 'imp', 'barh', figsize=(12,7), legend=False)
plot_fi(fi[:30]);The feature importance algorithm loops through each tree, and then recursively explores each branch. At each branch, it looks to see what feature was used for that split and how much the model improves as a result of that split. The improvement (weighted by the number of rows in that group) is added to the importance score for that feature. This is summed across all branches of all trees and finall the scores are normalized such that they add to 1.
Removing Low-Importance Variables
Retrain the model using the subset of columns with importance greater than 0.005:
to_keep = fi[fi.imp>0.005].cols
len(to_keep)20xs_imp = xs[to_keep]
valid_xs_imp = valid_xs[to_keep]
m = rf(xs_imp, y)m_rmse(m, xs_imp, y), m_rmse(m, valid_xs_imp, valid_y)(0.181078, 0.231864)Our accuracy is about the same with fewer columns that we have to study.
len(xs.columns), len(xs_imp.columns)(66, 20)Removing Redundant Features
from scipy.cluster import hierarchy as hc
def cluster_columns(df, figsize=(10,6), font_size=12):
corr = np.round(scipy.stats.spearmanr(df).correlation, 4)
corr_condensed = hc.distance.squareform(1-corr)
z = hc.linkage(corr_condensed, method='average')
fig = plt.figure(figsize=figsize)
hc.dendrogram(z, labels=df.columns, orientation='left', leaf_font_size=font_size)
plt.show()The pairs of columns that are most similar are the ones that were merged together early, far from the “root” of the tree at the left.
The most similar pairs are found by calculating the rank correlation, which means that all the values are replaced with their rank (first, second, third, etc within the column) and then the correlation is calculated.
Let’s try removing some of these closely related features to see if the model can be simplified without impacting accuracy.
Create a function that quickly trains a random forest and returns the OOB score by using a lower max_samples and higher min_samples_leaf.
def get_oob(df):
m = RandomForestRegressor(n_estimators=40, min_samples_leaf=15,
max_samples=50_000, max_features=0.5, n_jobs=-1, oob_score=True)
m.fit(df, y)
return m.oob_score_# baseline
get_oob(xs_imp)0.8764807857774278Remove each of our potentially redundant variables and see what score we get:
{c: get_oob(xs_imp.drop(c, axis=1)) for c in (
'saleYear', 'saleElapsed', 'ProductGroupDesc', 'ProductGroup',
'fiModelDesc', 'fiBaseModel',
'Hydraulics_Flow', 'Grouser_Tracks', 'Coupler_System')}{'saleYear': 0.875295601149204,
'saleElapsed': 0.8717546976024381,
'ProductGroupDesc': 0.8767983331719241,
'ProductGroup': 0.8764742908741526,
'fiModelDesc': 0.8748490763639009,
'fiBaseModel': 0.8760895658282863,
'Hydraulics_Flow': 0.8770549322909539,
'Grouser_Tracks': 0.8775175679664963,
'Coupler_System': 0.8764559009225574}Now let’s try dropping multiple variables:
to_drop = ['saleYear', 'ProductGroupDesc', 'fiBaseModel', 'Grouser_Tracks']
get_oob(xs_imp.drop(to_drop, axis=1))0.8751984884391564This is really not much worse than the model with all the fields so we’ll create DataFrames without these columns:
xs_final = xs_imp.drop(to_drop, axis=1)
valid_xs_final = valid_xs_imp.drop(to_drop, axis=1)# check accuracy
m = rf(xs_final, y)
m_rmse(m, xs_final, y), m_rmse(m, valid_xs_final, valid_y)(0.182723, 0.232926)Partial Dependence
Important to understand the relationship between the two most important predictors (ProductSize and YearMade) and sale price.
p = valid_xs_final['ProductSize'].value_counts(sort=False).plot.barh()
c = to.classes['ProductSize']
plt.yticks(range(len(c)), c);Partial dependence plots try to answer the question: if a row varied on nothing other than the feature in question, how would it impact the dependent variable?
How does YearMade impact sale price, all other things being equal? We can’t just take the average sale price for each YearMade, as it would capture the effect of how every other field also changed along with YearMade and how that overall change affected price.
Instead we replace every single value in the YearMade column with 1950, and then calculate the predicted sale price for every auction, and take the average over all auctions, then do the same for every single year. This isolates the effect of only YearMade.
from sklearn.inspection import partial_dependence
fig, ax = plt.subplots(figsize=(6,4))
pdp = partial_dependence(m, valid_xs_final, ['YearMade', 'ProductSize'],
grid_resolution=20)
ax.plot(array([0,1,2,3,4,5,6]), pdp['average'].mean(axis=1).squeeze());fig, ax = plt.subplots(figsize=(6,4))
ax.plot(pdp['values'][0], pdp['average'].mean(axis=2).squeeze());After 1990, where most of the data is, there is a linear relationship in the plot (y-axis is log(SalePrice) so this is an exponential relationship between YearMade and SalePrice). SalePrice has the lowest price for the last two categories (Large and #na#). This doesn’t make sense because I would expect the price to increase with ProductSize. Missing values can sometimes be useful predictors. Sometimes, they can indicate data leakage.
Data Leakage
Data leakage is the use of information in the model training process which would not be expected to be available at prediction time.
For example, if you are trying to predict successful grant applications using data that was not available at the time of receiving the application (such as information filled out only when a grant application was accepted such as date of processing).
Identifying data leakage involves building a model and then:
- Check whether the accuracy of the model is too good to be true.
- Look for important predictors that don’t make sense in practice.
- Look for partial dependence plot results that don’t make sense in practice.
It’s often a good idea to build a model first and then do your data cleaning, as the model can help you identify potentially problematic data issues.
Tree Interpreter
We still have to answer the following question:
- For predicting with a particular row of data, what were the most important factors, and how did they influence the prediction?
!pip install treeinterpreter
!pip install waterfallchartsWe computed feature importance across the entire random forest by looking at the contribution of each variable to improving the model, at each branch of every tree and then add up all of these contributions per variable.
We can do the same thing but for a single row of data. Let’s say we are looking at a single item at auction. The model might predict that this item will be very expensive, and we want to know why. Take the one row of data, put it through the first decision tree, looking to see what split is used at each point throughout the tree. For each split, we find the decrease or increase in the addition, compared to the parent node of the tree. We do this for every tree and add up the total change in importance by split variable.
row = valid_xs_final.iloc[:5]from treeinterpreter import treeinterpreter
prediction, bias, contributions = treeinterpreter.predict(m, row.values)prediction[0], bias[0], contributions[0].sum()(array([10.03216082]), 10.104110088290454, -0.0719492660421904)prediction is the prediction that the random forest makes. bias is the prediction based on taking the mean of the dependent variable (i.e. the model that is at the root of every tree). contributions is the the total change in prediction due to each of the independent variables. The sum of contributions plus bias must equal the prediction for each row.
Extrapolation and Neural Networks
Random forests, like all machine learning or deep learning algorithms, don’t always generalize well to new data.
The Extrapolation Problem
Consider the simple task of making predictions from 40 data points showing a slightly noisy linear relationship:
x_lin = torch.linspace(0,20,steps=40)
y_lin = x_lin + torch.randn_like(x_lin)
plt.scatter(x_lin, y_lin);sklearn expects a matrix of independent variables:
xs_lin = x_lin.unsqueeze(1)
x_lin.shape, xs_lin.shape(torch.Size([40]), torch.Size([40, 1]))x_lin[:, None].shapetorch.Size([40, 1])# use only the first 30 rows
m_lin = RandomForestRegressor().fit(xs_lin[:30], y_lin[:30])Test the model on the full dataset:
What we are seeing is that a tree and a random forest can never predict values outside the range of the training data, because a tree simply predicts the average value of the rows in a leaf and a random forest just averages the predictions of a number of trees. Your predictions outside the domain will be systematically too low. Random forests are not able to extrapolate outside the types of data they have seen in a more general sense, that’s why we need to make sure our validation set does not contain out-of-domain data.
Finding Out-of-Domain Data
Use a random forest to predict whether a row is in the validation set or the training set.
df_dom = pd.concat([xs_final, valid_xs_final])
is_valid = np.array([0]*len(xs_final) + [1]*len(valid_xs_final))
m = rf(df_dom, is_valid)
rf_feat_importance(m, df_dom)[:6]| cols | imp | |
|---|---|---|
| 6 | saleElapsed | 0.874998 |
| 9 | SalesID | 0.088186 |
| 12 | MachineID | 0.032512 |
| 0 | YearMade | 0.000888 |
| 5 | ModelID | 0.000784 |
| 11 | Enclosure | 0.000594 |
Three columns differ significantly between the training and validation sets: saleElapsed, SalesID, and MachineID. It makes sense that saleElapsed is different since it directly encodes date (number of days between the start of the dataset and each row) and the other two likely increment over time.
# baseline
m = rf(xs_final, y)
print('orig', m_rmse(m, valid_xs_final, valid_y))
for c in ('SalesID', 'saleElapsed', 'MachineID'):
m = rf(xs_final.drop(c, axis=1), y)
print(c, m_rmse(m, valid_xs_final.drop(c,axis=1), valid_y))orig 0.232669
SalesID 0.230199
saleElapsed 0.235264
MachineID 0.231392We should be able to remove SalesID and MachineID without losing accuracy:
time_vars = ['SalesID', 'MachineID']
xs_final_time = xs_final.drop(time_vars, axis=1)
valid_xs_time = valid_xs_final.drop(time_vars, axis=1)
m = rf(xs_final_time, y)
m_rmse(m, valid_xs_time, valid_y)0.229906Removing these variables has improved the accuracy and will make the model more resilient over time.
Try just using the most recent few years of the data:
filt = xs['saleYear']>2004
xs_filt = xs_final_time[filt]
y_filt = y[filt]
m = rf(xs_filt, y_filt)
m_rmse(m, xs_filt, y_filt), m_rmse(m, valid_xs_time, valid_y)(0.177093, 0.229919)Using a Neural Network
Replicate the steps to set up the TabularPandas object:
df_nn = pd.read_csv(path/'TrainAndValid.csv', low_memory=False)
df_nn['ProductSize'] = df_nn['ProductSize'].astype('category')
df_nn['ProductSize'].cat.set_categories(sizes, ordered=True, inplace=True)
df_nn[dep_var] = np.log(df_nn[dep_var])
df_nn = add_datepart(df_nn, 'saledate')FutureWarning: The `inplace` parameter in pandas.Categorical.set_categories is deprecated and will be removed in a future version. Removing unused categories will always return a new Categorical object.df_nn_final = df_nn[list(xs_final_time.columns) + [dep_var]]A great way to handle categorical variables in a neural net is with embeddings. Embedding sizes larger than 10,000 should generally be used only after you’ve tested whether there are better ways to group the variable, so use 9,000 as max_card (lower cardinality means fastai creates embedding for the categorical variable):
cont_nn, cat_nn = cont_cat_split(df_nn_final, max_card=9000, dep_var=dep_var)We don’t want to treat saleElapsed as categorical since we want to predict auction sale prices in the future and a categorical variable cannot extrapolate outside the range of values that it has seen:
'saleElapsed' in cont_nn, 'saleElapsed' in cat_nn(True, False)# look at cardinality
df_nn_final[cat_nn].nunique()YearMade 73
ProductSize 6
Coupler_System 2
fiProductClassDesc 74
Hydraulics_Flow 3
ModelID 5281
fiSecondaryDesc 177
fiModelDesc 5059
Hydraulics 12
Enclosure 6
fiModelDescriptor 140
ProductGroup 6
Drive_System 4
dtype: int64When analyzing redundant features relies on similar variables being sorted in the same order (they need to have similarly named levels). Here we see that ModelID and fiModelDesc both have 5000+ levels, meaning they would need 5000+ columns in our embedding matrix. Let’s see the impact of removing one of these model columns on the random forest:
xs_filt2 = xs_filt.drop('fiModelDesc', axis=1)
valid_xs_time2 = valid_xs_time.drop('fiModelDesc', axis=1)
m2 = rf(xs_filt2, y_filt)
m_rmse(m2, xs_filt2, y_filt), m_rmse(m2, valid_xs_time2, valid_y)(0.183026, 0.233514)xs_filt2 = xs_filt.drop('ModelID', axis=1)
valid_xs_time2 = valid_xs_time.drop('ModelID', axis=1)
m2 = rf(xs_filt2, y_filt)
m_rmse(m2, xs_filt2, y_filt), m_rmse(m2, valid_xs_time2, valid_y)(0.18152, 0.232451)Dropping ModelID has the smaller effect on accuracy so we’ll drop that variable.
cat_nn.remove('ModelID')df_nn_final[cat_nn].nunique()YearMade 73
ProductSize 6
Coupler_System 2
fiProductClassDesc 74
Hydraulics_Flow 3
fiSecondaryDesc 177
fiModelDesc 5059
Hydraulics 12
Enclosure 6
fiModelDescriptor 140
ProductGroup 6
Drive_System 4
dtype: int64A neural net cares about normalization whereas a random forest doesn’t:
procs_nn = [Categorify, FillMissing, Normalize]
to_nn = TabularPandas(df_nn_final, procs_nn, cat_nn, cont_nn, splits=splits, y_names=dep_var)Tabular models and data don’t generally require much GPU RAM so we can use larger batch sizes:
dls = to_nn.dataloaders(1024)Set y_range for regression models:
y = to_nn.train.y
y.min(), y.max()(8.465899, 11.863583)from fastai.tabular.all import *
learn = tabular_learner(dls, y_range=(8,12), layers=[500,250],
n_out=1, loss_func=F.mse_loss)
learn.lr_find()SuggestedLRs(valley=0.0002754228771664202)learn.fit_one_cycle(5, 1e-2)| epoch | train_loss | valid_loss | time |
|---|---|---|---|
| 0 | 0.062091 | 0.074148 | 00:08 |
| 1 | 0.054561 | 0.066272 | 00:04 |
| 2 | 0.048428 | 0.053494 | 00:06 |
| 3 | 0.043653 | 0.051082 | 00:04 |
| 4 | 0.040581 | 0.051459 | 00:05 |
preds, targs = learn.get_preds()
r_mse(preds, targs)0.226845The neural net is more accurate than the random forest.
tabular_learner??TabularModel??Ensembling
It would be reasonable to expect that the kinds of errors that each model makes (random forest and neural network) would be quite different. We might expect that the average of their predictions would be better than either one’s individual predictions.
rf_preds = m.predict(valid_xs_time)
ens_preds = (to_np(preds.squeeze()) + rf_preds) / 2r_mse(ens_preds, valid_y)0.223161This result is better than each individual model.
Boosting
bagging = combining many models (each trained on a different data subset) by averaging them.
boosting = add models instead of averaging them:
- Train a small model that underfits your dataset.
- Calculate the predictions in the training set for this model.
- Subtract the predictions from the targets; these are called the residuals and represent the error for each point in the training set.
- Go back to step 1, but instead of using the original targets, use the residuals as the targets for the training.
- Continue doing this until you reach a stopping criterion, such as maximum number of trees, or you observe your validation set error getting worse.
Each new tree will be attempting to fit the error of all the previous trees combined. The residuals get smaller and smaller each time. To make predictions, calculate the predictions from each tree and then add them all together. Most common model names: Gradient Boosting Machines(GBMs) and Gradient Boosted Decision Trees (GBDTs). XGBoost is the most popular library for implementing these.
Using more trees in a random forest does not lead to overfitting, because each tree is independent of the others. In a boosted ensemble, the more trees you have, the better the training error becomes and eventually you will see overfitting on the validation set. Unlike random forests, gradient boosted trees are extremely sensitive to the choices of hyperparameters.
Combining Embeddings with Other Methods
The embeddings obtained from the trained neural network boost the performance of all tested machine learning methods considerably when used as the input features instead. Models dramatically improve by using the neural network’s categorical embeddings instead of the raw categories as inputs.
At inference time, you can just use an embedding along with a small decision tree ensemble.
Once a set of embeddings are learned for a column for a particular task, they could be stored in a central place and reused across multiple models.
Conclusion
- Random forests are the easiest to train, because they are extremely resilient to hyperparameter choices and require little preprocessing. They are fast to train, and should not overfit if you have enough trees. But they can be a little less accurate especially if extrapolation is required, such as predicting future time periods.
- Gradient boosting machines in theory are just as fast to train as random forests, but in practice you will have to try lots of hyperparameters. They can overfit, but they are often a little more accurate than random forests.
- Neural networks take the longest time to train and require extra preprocessing, such as normalization; this normalization needs to be used at inference time as well. They can provide great results and extrapolate well, but only if you are careful with your hyperparameters and take care to avoid overfitting.
Start your analysis with a random forest. Then use that model for feature selection and partial dependence analysis, to get a better understanding of your data. Then try neural nets and GBMs and use them if they give significantly better results on your validation set in a reasonable amount of time. If decision tree ensembles are working well for you, try adding the embeddings for the categorical variables to the data and see if that helps your decision trees learn better.
Questionnaire
1. What is a continuous variable?
A variable that can take on any value within a range.
2. What is a categorical variable?
A variable that can only take on discrete values or levels within a fixed set.
3. Provide two of the words that are used for the possible values of a categorical variable.
Levels or categories.
4. What is a dense layer?
A linear layer.
5. How do entity embeddings reduce memory usage and speed up neural networks?
They are dense compared to one-hot-encoded vectors which are sparse.
6. What kinds of datasets are entity embeddings especially useful for?
Datasets with categorical variables with high cardinality.
7. What are the two main families of machine learning algorithms?
- Ensembles of decision trees for structured data.
- Multilayered neural networks learned with SGD for unstructured data.
8. Why do some categorical columns need a special ordering in their classes? How do you do this in Pandas?
Ordinal columns have a natural order (like size) and can be specified using the Series.cat.set_categories Pandas method.
9. Summarize what a decision tree algorithm does.
A decision tree algorithm loops through each column and for each column loops through all possible splits in the data, and calculates the objective (such as average SalePrice) for each group in the split. It then splits the data with the best split, meaning the split that has the highest average objective. Within each split, it continues to split the data and calculate the next best split until some stopping criteria is met.
10. Why is a date different from a regular categorical or continuous variable, and how can you preprocess is to allow it to be useful in a model?
Dates have many meanings such as day of the week, the month it’s in and whether it’s a holiday. You can preprocess a date variable with fastai’s add_datepart function.
11. Should you pick a random validation set in the bulldozer competition? If no, what kind of validation set should you pick?
No. Since we want to predict auction price for future dates, the validation set should have date values that come after the training set dates.
12. What is pickle and what is it useful for?
Pickle is a method to save (serialize) Python objects.
13. How are mse, samples, and values calculated in the decision tree drawn in this chapter?
The mse is calculated between the average sale price and the individual sale price in the group. samples are the number of rows in the dataset that correspond to the given split that resulted in the group. values is the average sale price in the group.
14. How do we deal with outliers before building a decision tree?
Decision trees are resilient to data issues but if you want to treat outliers you can do so by setting their value to a more reasonable value (as we did by setting any YearMade value less than 1900 to 1950.
15. How do we handle categorical variables in a decision tree?
We don’t have to handle them in anyway other than encoding them as integers. Research shows that one-hot-encoding categorical variables doesn’t improve model performance.
16. What is bagging?
Averaging predictions across multiple models that are trained on different subsets of the dataset. Since different models make different errors, the average of the errors is zero.
17. What is the difference between max_samples and max_features when creating a random forest?
max_samples is the maximum number of rows to sample for each decision tree.
max_features defines how many columns to sample at each split point.
18. If you increase n_estimators to a very high value, can that lead to overfitting? Why or why not?
No, because decision trees are trained on a subset of data independent from each other.
19. In the section “Creating a Random Forest”, after Figure 9-7, why did preds.mean(0) give the same result as our random forest?
Since the random forest does the same thing: take the average prediction across all trees.
20. What is out-of-bag error?
The error of a tree’s prediction on rows from the dataset that it has not been trained on.
21. List the reasons that a model’s validation set error might be worse than the OOB error. How could you test your hypotheses?
It could be that the model does not generalize well to data other than the training set. It could also mean that the distribution of the validation set is different from the training set (which can be tested by training a random forest on is_valid–1/0 whether the data is validation/train and seeing which features have high importance).
22. Explain why random forests are well suited to answering each of the following questions:
- How confident are we in our predictions using a particular row of data?
- This is answered by calculating the standard deviation of the trees’ predictions for each row in the validation set.
- For predicting with a particular row of data, what were the mot important factors, and how did they influence that prediction?
- Using
treeinterpreterwe can see how much each column contributed to the total change in prediction.
- Using
- Which columns are the strongest predictors?
- This is answered by calculating the feature importance, which is the (weighted by number of rows in each branch group) improvement to the model made by each feature.
- How do predictions vary as we vary these columns?
- We can look at partial dependence plots to answer this question.
23. What’s the purpose of removing unimportant variables?
To simplify the model so that we can understand and study how each feature influences the predictions.
24. What’s a good type of plot for showing tree interpreter results?
Waterfall charts.
25. What is the extrapolation problem?
Random forests and trees can never predict values outside the range of the training data. Predictions in this case will systematically be too low.
26. How can you tell if your test or validation set is distributed in a different way than your training set?
By training a random forest where the dependent variable is is_valid a field that is 1 for rows in the validation set and 0 for rows in the training set, and then calculating feature importance. Features with the highest importance will differ in value between the training and validation set.
27. Why do we make saleElapsed a continuous variable, even though it has fewer than 9,000 distinct values?
saleElapsed is the number of days since the start of the dataset that the auction took place, so it represents date/time of the auction. Since we want to extrapolate auction prices to future dates, we want to treat it as something that can be extrapolated (continuous variable) as opposed to something that can’t be extrapolated (categorical variable).
28. What is boosting?
Boosting is when you train a model to underfit the dataset and train subsequent models on residuals (difference between targets and predictions) and then add together the predictions from the models.
29. How could we use embeddings with a random forest? Would we expect this to help?
Research shows that using neural net trained categorical embeddings as inputs (instead of categorical columns) improves the accuracy of random forests.
30. Why might we not always use a neural net for tabular modeling?
Neural nets take the longest time to train (compared to random forests and gradient boosting), require preprocessing and are sensitive to hyperparameters.
Lesson 6: Random Forests
- Further Research
- Pick a competition on Kaggle with tabular data (current or past) and try to adapt the techniques seen in this chapter to get the best possible results. Compare your results to the private leaderboard.
- Implement the decision tree algorithm in this chapter from scratch yourself, and try it on the dataset you used in the first exercise.
- Use the embeddings from the neural net in this chapter in a random forest, and see if you can improve on the random forest results we saw.
- Explain what each line of the source of
TabularModeldoes (with the exception ofBatchNorm1dandDropoutlayers).
Video Notes
How random forests really work
- We created binary splits in the Titanic dataset for continuous and categorical variables.
- We came up with a score of how good a job did that split do of grouping the survival characteristics into two groups where nearly all of one survived and all of one didn’t survive. Small (weighted) standard deviation in each group.
- What if we split Males and Females into two other groups each?
- Age <=6 is the biggest predictor of whether males survive.
- Pclass <= 2 is the biggest predictor of whether females survive.
- We hope to get the strongest prediction about survival in the leaf nodes of our decision tree.
- We use sklearn’s
DecisionTreeClassifier. - scikit-learn focuses on classical machine learning algorithms.
- Decision trees as exploratory data analysis: allows us to get a quick picture of what are the key driving variables in this dataset and how much do they predict what was happening in the data.
- gini is another way of measuring how good a split is: how likely is it that if you go into that sample and grab one item and then go in again and grab another item—how likely is it that you’re going to grab the same item each time? If the entire leaf node is just people who survived or just people who didn’t survive, the probability would be 1.0. If it was an exactly equal mix the probability would be 0.5.
- OneR MAE was 0.215, decision tree with four leaf nodes’ MAE was 0.224. Reflects the fact that we have a small validation set.
- Decision tree with minimum samples of 50 per node has MAE of 0.183.
- One of the biggest mistakes is not to submit to the leaderboard on Kaggle for a competition. You should try and submit something to the leaderboard everyday.
- We don’t need to do as much preprocessing for decision trees. All the decision tree cares about is the ordering of the data.
- For tabular data, always start with a decision tree approach.
- Use dummy variables for <= 4 levels, numeric codes otherwise.
- There are limitations to how accurate a decision tree can be.
- Leo Breiman came up with the idea of bagging. Decision trees on average will predict the average, they are not biased. Build lots of unbiased, better-than-nothing, uncorrelated models, and average their predictions, ending up with errors on either side of the correct prediction whose average is 0. So it will be better than any individual model.
- We can get many trees who use some random proportion of rows and columns (called a random forest), make predictions with each of them, and then average the predictions.
- In each splot of each decision tree in the random forest you can calculate how much the prediction improved (e.g., how much gini value reduced weighted by sample size) on a split by the given column. This gives you the feature importances—how often did the trees pick the feature and how much did it improve the gini when picked as a split?
- Create a feature importance plot first with a tabular dataset to find the most important columns.
- Rule of thumb: use a maximum of 100 trees.
- If you don’t have much data you can get away with not having a validation set since for each tree in the random forest you can pick the rows not used in that tree as the validation set. The error across all rows not used in training a tree is called out-of-bag (OOB) error.
- Five important insights random forests can provide:
- How confident are we in our predictions using a particular row of data?
- For predicting with a particular row of data, what were the most important factors, and how did they influence that prediction?
- Which columns are the strongest predictors and which can we ignore?
- Which columns are effectively redundant with each other, for purposes of prediction?
- How do predictions vary, as we vary these columns?
- You can do a partial dependence plot for any machine learning model.
- Take the dataset and leave it exactly as it is except for the column you want to understand partial dependence on (such as
YearMade). Set the column in question to its first value, then predict the dependent variable for every row and average it. Repeat for each value of the column in question.
- Take the dataset and leave it exactly as it is except for the column you want to understand partial dependence on (such as
- You can do feature importance for one row to understand why the random forest made the prediction.
- If you start deleting trees then you are no longer having an unbiased prediction of the dependent variable. You are biasing it by making a choice. Even the bad trees will be improving the quality of overall average.
- Can you overfit a random forest? Basically no. Adding more trees will make it more accurate,but accuracy asymptotes. If you don’t have enough trees and you let the trees grow very deep, that could overfit, so you have to make sure you have enough trees.
- Giving a random forest lots of randomly generated columns with fake data does not affect its performance.
- Gradient boosting machine: fit a very small tree, get the residual (the difference between the prediction and the actual), then create another very small tree which attempts to predict the residual and so forth. Each one is predicting the residual from all the previous ones. Then to calculate the prediction you take the sum of all of the trees’ predictions, because each one has predicted the difference between the actual and all of the previous trees. More accurate than random forests, but you can absolutely overfit, so it’s not the first go-to model.
First Steps: Road to the top, Part 1
- What does it look like to pick a Kaggle competition and just do like the normal, sensible, mechanical steps you would do for any computer vision model.
- Paddy Disease Classification: recognizing diseases in rice paddies.
- The library
fastkagglemakes it easier to setup Kaggle competition stuff. Usesetup_compto grab data. - You can’t hide from the truth in a Kaggle competition.
- Focus on two things:
- Creating an effective validation set.
- Iterating rapidly to find changes which improve results on the validation set.
- What can I do that’s going to train in a minute or so and will quickly give me a sense of what I can try and what’s going to work. Try 80 things.
- Do be successful in Kaggle competitions and machine learning in general you have to do not just one thing well but everything well.
- Only use random seed when you are sharing a notebook, otherwise you want to see how much things change each time so you can tell if the modifications you are making are improving it, making it worse, or is it just random variation?
- PIL images size is columns x rows. PyTorch size is rows x columns.
- The amount of time it takes to decode a JPEG is quite significant. Use
fastcore.parallel. - Most common way to do things is to either squish or crop every image to be a square.
- Models are a great way to understand your data. Refer to the notebook The best vision models for fine tuning—trained on PETS (fine-tuning to similar things they are pretrained on) and Planet (fine-tuning to things different than what is pretrained) datasets which are very different datasets. Measured how much memory it used, how accurate was it and how long did it take to fit.
- What matters about a model, which is just a function, is its inputs, outputs how accurate it is and how fast it is.
lr_findwill train one batch a time and track the loss at increasing learning rates (starting very small). LR recommendations are conservative.- We submit as soon as we can. We want a dataloader that is exactly like what we made for training but pointed at the test set. Use
dls.test_dlmethod. Pass it test dataset files. A test dataloader does not have any labels. with_decodedinlearn.get_predstells you the index of the most probably class. Map them to strings indls.vocab.- Make everything fast and easy in the iteration including submitting to Kaggle.
- If you can create models that predict things well and you can communicate your results in a way that is clear and compelling, you’re a pretty good data scientist.
- Be highly intentional like a scientist; have hypotheses that you test carefully and come out with conclusions that you implement.
- Test out your hypotheses over a couple models from each of the main families (e.g., does squish or crop work better with different models).
- Random forests will give you good results, GBMs for better results (would run a hyperparameters sweep).
Small Models: Road to the top, Part 2
- Initial training took a minute on home computer, took 4 minutes per epoch on Kaggle. Because they only have two virtual CPUs. You want at least 8 physical CPUs per GPU. It was spending all its time reading data.
- Step 1 was making Kaggle implementation faster—
resize_images. It was four times faster with no loss of accuracy. - Kaggle GPU was hardly being used so moved from
resnet26dtoconvnext_small_in22kwhich was over twice as good. - resnets are the fastest, use convnext if you’re not sure what to use.
- Use crop instead of squish.
- Get everything for training into a single function that returns a
learner. - Padding is the only way of preprocessing images that doesn’t distort (squish) or lose data (crop) with the downsize of having empty black pixels.
- Test time augmentation (TTA). Get preditions for all augmented images and take the average. Like a mini-bagging approach.
learn.ttadoes this for you. TTA usually gives a better result. TTA uses the same data augmentation that you used during training. - Your images don’t have to be square. They just have to be the same size.
idxshas indexes of vocab for each test set image,vocabisnp.array(learn.dls.vocab,resultsispd.Series[vocab[idxs], name='idxs)will map index to vocab item.- Generally speaking in Kaggle competitions, top 25% is a solid, competent, very reasonable level. It’s not easy, you gotta know what you’re doing.
- Batch things that are similar aspect ratios together and use the median rectangles for those and have had good results but honestly 99.99% of people chuck everything into a square.
- fastai uses reflection padding as a default, also provide copy padding, neither really help. Computer wants to know where the image ends.
Lesson 7: Collaborative Filtering
Video Notes
- Digging into what’s inside of a neural net in this lesson.
- A neural net has a sandwich of fully connected layers and ReLUs. There’s a lot of tweaks that we can do. Most of the tweaks we care about are tweaking the very first or the very last layer. Over the next couple of weeks we’ll look at the tweaks we can do inside as well.
Paddy Doctor Competition
- Created a ConvNeXt model. Did a few types of preprocessing. Added Test Time Augmentation. Scaled that up to larger images and rectangular images.
- Larger models have more parameters which means they can learn more tricky features. And they ought to be more accurate. The also take up more memory on the GPU when calculating gradients. The GPU is not as clever as the CPU at sticking stuff it doesn’t need right now onto virtual memory on the hard drive. When it runs out of memory, it runs out of memory. It also doesn’t shuffle things around to try and find memory, it just allocates blocks of memory that stay allocated until you remove them.
- If you get a CUDA Out-Of-Memory error, restart your notebook. Tricky to recover from otherwise.
- Will I be able to train on 16GB? One way to quickly do that is train only on one label and see how much memory it used.
- Call python’s garbage collection
gc.collect()and PyTorch’storch.cuda.empty_cache()will get GPU back to a clean state. - If you run out of memory—use
GradientAccumulation. Using a small batch size (bs = 16instead ofbs = 64) will solve the memory problem but will change the dyanmics of the training since the smaller your batch size the more volatility there is, so now your learning rates need to change. You don’t want to mess around trying to find different hyparameters for every batch size for every architecture.GradientAccumulation(bs)makes the training behave as if the batch size isbseven when it’s not. - Consider the training loop:
for x,y in dl:
calc_loss(coeffs, x, y).backward()
coeffs.data.sub_(coeffs.grad * lr)
coeffs.grad.zero_()- Note that you don’t need
with torch.no_grad()since you are usingcoeffs.data. - Here’s a variation of that loop with
GradientAccumulationadded:
count = 0 # track count of items seen since last weight update
for x,y in dl:
count += len(x) # update count based on this minibatch size
calc_loss(coeffs, x, y).backward()
if count >= 64: # count is greater than accumulation target so do weight update
coeffs.data.sub_(coeffs.grad * lr)
coeffs.grad.zero_()
count = 0 # reset count- In PyTorch if you call
backward()without zeroing the gradients then it adds new gradients to old gradients. - Doing two half-size batches without zeroing out between them is adding up the gradients.
- You don’t need to buy a bigger GPU to train bigger models. Just use
GradientAccumulation. GradientAccumulationis numerically identical for some architectures. Other architectures use batch normalization (which keeps track of the moving average of standard deviation and averages and does it in a mathematically slightly incorrect way). UsingGradientAccumulationwith batch normalization can introduce more volatility. Which is not necessarily a bad thing but it’s not numerically identical so you won’t get the same results.lr_finduses yourDataLoadersbatch size.- Pick the largest batch size that you can (you’re getting more parallel processing). Generally a good idea for it to be a multiple of 8 for performance reasons.
- In fastai use
GradientAccumulationby passing it as acbs(callback)
cbs = GradientAccumulation(<effective batch size>)
learn = vision_learner(dls, arch, metrics, cbs=cbs)- For bigger models you’ll get to a linear scaling with
GradientAccumulation. Models have a bit of an overhead. - Nearly all transformer models have a fixed input size.
- Use different training sets (i.e. don’t set
seedin the validation splitter) when you are going to ensemble. - A popular thing is to do k-fold cross validation. 5-fold CV does something similar to what Jeremy did with training on a random 80% split. In theory that could be slightly better because you’re guaranteed that every row appears four times. Also has the benefit that you can average those five validation sets that have no overlap. Jeremy usually doesn’t bother because this way he can add or remove models very easily.
- NVIDIA consumer cards (RTX) are just as good as enterprise cards. NVIDIA will not allow you to use an RTX card in a data center. Which is why cloud computing is more expensive.
- teacher-student models and model distillation—there are ways to make inference faster by training small models that work the same way as large models.
- Build a model to predict both disease and variety of rice. The first thing you need is a
DataLoadersthat have two dependent variables:
dls = DataBlock(
blocks=(ImageBlock, CategoryBlock, CategoryBlock),
n_inp=1, # otherwise it doesn't know which of the 3 is ind/dep var
get_items=get_image_files,
get_y = [parent_label, get_variety],
splitter = RandomSplitter(0.2, seed=42),
item_tfms = Resize(192, method='squish'),
batch_tfms = aug_transforms(size=128, min_scale=0.75),
).dataloaders(path)- Jeremy first create a
DataBlockthat did exactly the same thing as the single-dependent-variable disease-classifier and then once he got that to work, expanded it to two dependent variables. - In pandas you can set one column to be the index:
df = pd.read_csv(path/'train.csv', index_col='image_id')So that you can then use df.loc['100330.jpg', 'variety'] to get the variety column for a given image_id. You can then wrap this into a function to use for get_y:
def get_variety(p): return df.loc[p.name, 'variety']Where p is a Path object.
- How do we get a model that predicts two things? We never had a model that predicted one thing, we had a model that predicts 10 things (probabilities for 10 disease classes). We want a model that now predicts 20 things.
- fastai will pass to metrics and loss function three things: the input and two dependent variables. Can’t just use
error_rateas metric since that takes only two inputs. Instead have to create a custom metric that takes three inputs and returns the error rate for disease-only (same thing for loss):
def disease_err(inp, disease, variety): return error_rate(inp, disease)
def disease_loss(inp, disease, variety): return F.cross_entropy(inp, disease)- The stuff in the middle of the model, you’re going to think about that much but the stuff at the ends you think about a lot.
- Cross Entropy Loss example: assume you have a mini imagenet with 5 classes (cat, dog, plane, fish, building):
| output | exp | softmax | actuals | index | |
|---|---|---|---|---|---|
| cat | -4.89 | 0.01 | 0.00 | 0 | 1 |
| dog | 2.60 | 13.43 | 0.87 | 1 | 1 |
| plane | 0.59 | 1.81 | 0.12 | 0 | 2 |
| fish | -2.07 | 0.13 | 0.01 | 0 | 3 |
| building | -4.57 | 0.01 | 0.00 | 0 | 4 |
- output is the output from the model (5 values for 5 classes). They’re not probabilities yet, they’re just 5 numbers. We want to convert these into probabilities.
Softmax: \[\frac{e^{z_i}}{\sum_{j=1}^K e^{z_j}}\]
- We’re going to go through each of the categories (1 to K = 5). Take \(e\) to the power of the output (\(z\)). Sum them all together. That’s the denominator. The numerator is \(e\) to the power of the thing that we care about (each row). The sum of these fractions is 1. Now we have things that are probabilities: numbers that are between 0 and 1 and add up to 1.0. Since we did \(e\) to the power of the output, the bigger outputs will be pushed up closer to 1.0. We’re making the model really try to pick one thing. There’s no way for it to predict anything other than the categories we are giving it. We are forcing it to pick one. You can have the probabilities add up to more than one (more than one thing being true) or less than one (no things being true).
- The first part of what
nn.CrossEntropydoes it to calculate the softmax. It’s actually the log of the softmax. - Now that we have the 5 probabilities, the next step is the actual cross-entropy calculation:
| softmax | actuals | x-entropy | |
|---|---|---|---|
| cat | 0.00 | 0 | 1 |
| dog | 0.87 | 1 | 1 |
| plane | 0.12 | 0 | 2 |
| fish | 0.01 | 0 | 3 |
| building | 0.00 | 0 | 4 |
- The actuals are one-hot encoded (1 for the thing that is True and 0 everywhere else).
- We would expect a smaller loss where the softmax is high if the actual is high. Formula for cross-entropy:
\[-\sum_{j=1}^M y_j\log(p(y_j))\]
- Where \(y_j\) is an indicator variable and \(p(y_j)\) is the predicted probability (the softmax column). Cross entropy is then -log(softmax). For four classes that value is 0. That equation is finding the probablity for the class that is 1 and taking its log.
- Here’s the equation for binary cross-entropy:
\[-\sum_{i=1}^N y_i \log(p(y_i)) + (1 - y_i)\log(1 - p(y_i))\]
- Where \(y_i\) is the label, and \(p(y_i)\) is the probability of the positive class. \(y_i=1\) if it is a cat, \(y_i=0\) if it is not a cat.
- PyTorch loss functions have two versions:
nnClass which you can instantiate passing in various tweaks and theFfunction that doesn’t allow these tweaks. - When you have multiple targets you can’t rely on fastai to know what loss function to use so you have to pass your custom loss function to the
loss_funcparameter in the learner. Same for metrics. Also, fastai no longer knows how many activations to create because there is more than one target so you have to pass a value ton_outwhich is the number of targets (the size of the last matrix). - For two-target situation, we have to set
n_outto20when creating the learner since 10 of those targets are for disease and 10 are for variety of rice. How does the model know what it’s predicting? The answer is: with the loss function—you’re going to have to tell it.inpis going to have 20 columns (sincen_outis 20) so we’re just going to have to decide that the first 10 columns correspond to the disease predictions.
def disease_loss(inp, disease, variety): return F.cross_entropy(inp[:,:10], disease)- For variety, we use the second ten columns:
def variety_loss(inp, disease, variety): return F.cross_entropy(inp[:,10:], variety)- The overall loss function is the sum of those two things:
def combine_loss(inp,disease,variety): return disease_loss(inp,disease,variety)+variety_loss(inp,disease,variety)As the model trains, this loss function will be minimized when the first ten columns are doing a good job at predicting disease probabilities and the second ten columns are doing a good job at predicting variety probabilities. Therefore the gradients will point in the appropriate direction, the coefficients will get better and better at using those columns for those purposes.
- Do the same for
error_rate:
def disease_err(inp,disease,variety): return error_rate(inp[:,:10],disease)
def variety_err(inp,disease,variety): return error_rate(inp[:,10:],variety)
err_metrics = (disease_err,variety_err)- the
Learnerlooks like:
learn = vision_learner(dls, arch, loss_func=combine_loss, metrics=err_metrics, n_out=20)It was slightly less good at predicting disease but that makes sense because we have trained it for the same number of epochs (5 in this case) but have given it more stuff to do.
If we train it for longer, this model might end up getting better at predicting disease than the single-label disease model. It turns out quite often that the kind of features that help you recognize variety of rice also help recognize disease, maybe there are certain textures, or maybe some diseases impact different varieties in different ways.
Build a model that predicts two things in the Titanic dataset.
Look at the inputs and outputs of the multi-target part 4 notebook.
Collaborative Filtering Deep Dive
- This kind of data is very common:
| user | movie | rating |
|---|---|---|
| 196 | 242 | 3 |
| 186 | 302 | 3 |
| 22 | 377 | 1 |
| 244 | 51 | 2 |
| 166 | 346 | 1 |
Anytime you have a user and product you’ll have this kind of data. What happens when the rating is blank? How do you fill it in? To figure this out, ideally we’d like to know for each movide: what kind of movie is it? What are the features of it? If we had three categories: science-fiction, action and old movies, then Last Skywalker would be represented by the following (where each value ranges from -1 to 1):
last_skywalker = np.array([0.98, 0.9, -0.9])It’s very science-fictiony, very action-y and very not old.
A user who liked modern sci-fi could be represented by:
user1 = np.array([0.9, 0.8, -0.6])To calculate the match between last_skywalker and user1 we can multiple the values and sum:
(user1*last_skywalker).sum() # = 2.142- On the other hand, the movie Casablanca, not science-fiction, not really very action, and very much an old classic:
casablanca = np.array([-0.99, -0.3, 0.8])- On the other hand, the movie Casablanca, not science-fiction, not really very action, and very much an old classic:
casablanca = np.array([-0.99, -0.3, 0.8])- Matching it with the user:
(user1*casablanca).sum() # -1.611- Multiplying the corresponding elements of two vectors and adding them up is called dot product. The above is a dot product of the users preferences and a type of movie. The problem is we weren’t given this information about users and movies. What we can do is create things called Latent Factors: I don’t know what things about movies matter to people, but there’s probably something, and let’s just try using SGD to find them. We can do it in Microsoft Excel!
- In Excel we create 5 latent factors (rows) of random numbers for each movieId and userId. We don’t know what these represent but they represent something. Only quirk is that if the actual rating is blank we’re going to set the dot product to 0 by default.
- The matrix product of a row and a column is the same thing as a dot product. These dot products are everybody’s predicted ratings for movies. They are terrible predictions since the latent factors are just random numbers, but they are predictions nonetheless.
- When we have predictions using random numbers, we know how to make them better: stochastic gradient descent. To do that we need a loss function: RMSE = square root of sum of x minus y squared divided by the count (in Excel: =SQRT(SUMXMY2()/COUNT()))
- Excel solver: minimize cell with loss by changing userId and movieId latent factors. In Jeremy’s workbook: starts at 2.81 and ends at 0.42. In my workbook: starts at 2.92 and ends up at 0.43 after Solver is run.
- The cosine of the angle between vectors is the same as the normalized dot product.
- Using embeddings: replicating what we’ll have in Python which is a table with rows userid, movieid and rating. We’ll get the embeddings for each userid and the embeddings for each movieid all in one row, and then use Excel function SUMPRODUCT (which is dot product) to get the prediction. This is the same as before but when we put everything next to each other we have to lookup the index of userId and movieId and then lookup the embeddings.
- For each row calculate the error squared (pred-rating)^2 and take the square root of the average of error squareds to get the rmse, which is 2.71 in my case (Jeremy used the same random initial numbers for the dot product tab and the movielens_emb tab).
- Running solver: my rmse goes from 2.71 to 0.443 which is about the same as before (with different randomly initiated embeddings).
- What is an embedding? It’s just looking something up in an array.
- How do we do this in PyTorch? We’re going to need
DataLoaders.
movies = pd.read_csv(path/'u.item', delimiter='|', encoding='latin-1', usecols=(0,1), names=('movie', 'title'), header=None)movies.head() outputs:
| movie | title | |
|---|---|---|
| 0 | 1 | Toy Story (1995) |
| 1 | 2 | GoldenEye (1995) |
| 2 | 3 | Four Rooms (1995) |
| 3 | 4 | Get Shorty (1995) |
| 4 | 5 | Copycat (1995) |
Merge this with ratings so we can get the movie titles:
ratings = pd.read_csv(path/'u.data', delimeter='\t', header=None, names=['user', 'movie', 'rating', 'timestamp'])ratings.head() outputs:
| user | movie | rating | timestamp | |
|---|---|---|---|---|
| 0 | 196 | 242 | 3 | 881250949 |
| 1 | 186 | 302 | 3 | 891717742 |
| 2 | 22 | 377 | 1 | 878887116 |
| 3 | 244 | 51 | 2 | 880606923 |
| 4 | 166 | 346 | 1 | 886397596 |
Merge with movies to get title:
ratings = ratings.merge(ratings)ratings.head() output:
| user | movie | rating | timestamp | title | |
|---|---|---|---|---|---|
| 1 | 63 | 242 | 3 | 875747190 | Kolya (1996) |
| 2 | 226 | 242 | 5 | 883888671 | Kolya (1996) |
| 3 | 154 | 242 | 3 | 879138235 | Kolya (1996) |
| 4 | 306 | 242 | 5 | 876503793 | Kolya (1996) |
Next we create the DataLoaders with CollabDataLoaders which expects a user column and item column where item is the service or product that the user is rating. By default the user column should be called user and the item column called item.
dls = CollabDataLaoders.from_df(ratings, item_name='title', bs=64)dls.show_batch() outputs:
| user | title | rating | |
|---|---|---|---|
| 0 | 518 | Richard III (1995) | 3 |
| 1 | 546 | Star Wars (1977) | 5 |
| 2 | 264 | Adventures of Priscilla, Queen of the Desert, The (1994) | 4 |
| 3 | 201 | Kolya (1996) | 4 |
| 4 | 664 | Dances with Wolves (1990) | 3 |
| 5 | 391 | Jerry Maguire (1996) | 4 |
| 6 | 401 | Beauty and the Beast (1991) | 2 |
| 7 | 771 | Strictly Ballroom (1992) | 5 |
| 8 | 330 | 101 Dalmatians (1996) | 4 |
| 9 | 594 | One Flew Over the Cuckoo’s Nest (1975) | 4 |
Now we’re going to create the user factors and movie factors (i.e. the two embedding matrices we created in the Excel file). The number of rows of movie factors is equal to the number of movies and the number of columns will be whatever we want (however many factors we want to create). How many factors to use? Jeremy wrote down how many factors he thought was appropriate for different sized categories in Excel and fitted a function to that and that’s the function fastai uses—a mathematical function that fits Jeremy’s intuition about what works well. It’s pretty fast to train these things so you can try a few.
n_users = len(dls.classes['user'])
n_movies = len(dls.classes['title'])
n_factors = 5
user_factors = torch.randn(n_users, n_factors)
movie_factors = torch.randn(n_movies, n_factors)Now we need to lookup the index of our movie in our movie latent factor matrix (and user index for the user latent factor matrix). When we’ve learned about deep learning we’ve learned about matrix multiplication, not look-something-up-in-a-matrix. In Excel we were using OFFSET which can actually be represented as matrix multiplication. “Find this element in this list” is the same as matrix multiplying a one-hot-encoded vector. Taking the dot product of a one-hot-encoded vector with another vector is the same as looking up that index in the vector.
one_hot_3 = one_hot(3, n_users).float()is a vector where the 3rd element is set to 1 and everything else is set to 0s.
If we matrix multiply that by our user_factors transposed:
user_factors.t() @ one_hot_3We get tensor([-1.2493, -0.3099, 1.4229, 0.0840, 0.4132])
which is the same as the vector at index 3 in the matrix:
user_factors[3]
You can think of an embedding as a computational shortcut for multiplying something by a one-hot-encoded vector. It’s like dummy variables (without having to create the dummy variables). We never have to create a one-hot-encoded vector, we can just look up an array.
- Building a collaborative filtering model from scratch
In PyTorch, a model is a class. Example:
class Example:
def __init__(self, a): self.a = a
def say(self, x): return f'Hello {self.a}, {x}.'__init__ is called when you create an object of the given class.
ex = Example('Sylvain')
ex.say('nice to meet you')outputs:
'Hello Sylvain, nice to meet you.'
You can put something in parenthesis after your class name, the super class, which will give you some functionality for free. A PyTorch model has to have Module as its super class. fastai also has its own Module class. Here’s a DotProduct class:
class DotProduct(Module):
def __init__(self, n_users, n_movies, n_factors):
self.user_factors = Embedding(n_users, n_factors)
self.movie_factors = Embedding(n_movies, n_factors)
def forward(self, x):
users = self.user_factors(x[:,0])
movies = self.movie_factors(x[:,1])
return (users * movies).sum(dim=1)PyTorch calls a forward method when you call a model object. This is where you put the calculation of your model. dim=1 because we are summing across the columns for each row in the batch–a prediction for each row. We can now pass the model to the Learner:
model = DotProduct(n_users, n_movies, 50)
learn = Learner(dls, model, loss_func=MSELossFlat())Then we cant train:
learn.fit_one_cycle(5, 5e-3)
This runs on CPU and takes about 10 seconds per epoch (100k rows) and gets to 0.86 loss after 5 epochs. A whole lot faster than our few dozen rows in Excel. It’s not a great model. One problem is that some of the predictions are greater than 5.
When we add sigmoid, it squishes things to between 0 and 1 so the model doesn’t have to work so hard to get the predictions into the right zone. If you pass something through sigmoid and multiply it by 5, now you’re going to get something between 0 and 5. Use sigmoid_range to do that:
class DotProduct(Module):
def __init__(self, n_users, n_movies, n_factors, y_range=(0,5.5)):
self.user_factors = Embedding(n_users, n_factors)
self.movie_factors = Embedding(n_movies, n_factors)
self.y_range = y_range
def forward(self, x):
users = self.user_factors(x[:,0])
movies = self.movie_factors(x[:,1])
return sigmoid_range((users * movies).sum(dim=1), *self.y_range)Why not use upper limit of 5? That’s because sigmoid can never hit 1. So sigmoid times 5 can never hit 5. In this case, this didn’t improve the loss.
Some users just loved movies–they give everything 4s and 5s. Some people’s ratings have much more range (1s, 2s, 5s). Some people give nothing a 5. At the moment we don’t have any way in our formulation of this model to say this user tends give low scores and this user tends to give high scores. That would be very easy to add. Let’s add one more number to our 5 factors. Now instead of just matrix multiplying, let’s add this number to it. Matrix multiplication plus user bias plus movie bias. Effectively that’s making it so that we don’t have an intercept of 0 anymore. Implementing this in my Excel dropped the loss from 0.43 to 0.40.
Here’s the PyTorch version:
class DotProductBias(Module):
def __init__(self, n_users, n_movies, n_factors, y_range=(0,5.5)):
self.user_factors = Embedding(n_users, n_factors)
self.user_bias = Embedding(n_users, 1)
self.movie_factors = Embedding(n_movies, n_factors)
self.movie_bias = Embedding(n_movies, 1)
self.y_range = y_range
def forward(self, x):
users = self.user_factors(x[:,0])
movies = self.movie_factors(x[:,1])
res = (users * movies).sum(dim=1, keepdim=True)
res += self.user_bias(x[:,0]) + self.movie_bias(x[:,1])
return sigmoid_range(res, *self.y_range)In Jeremy’s case, this made the training worse (the loss increased) and the validation loss started increasing after the second epoch—we might be overfitting. One way to avoid overfitting is to use weight decay (also known as L2 regularization). When we compute the gradients we’ll add to our loss function the sum of the weights squared (times some small number). What would make that loss function go down? If we reduce the magnitude of our weights. For example if we reduce all of our weights to 0, that part of the los function will be 0. The problem is, if our weights are all 0, our model doesn’t do anything. So we want it to increase the weights. But if it increases the weights too much, then it starts overfitting. How is it going to actually get the lowest value of the loss function? By finding the right mix. Weights not too high but high enough to be useful for predicting. If there’s some paramter that’s not useful, it can just set the weight to 0. It won’t be used to predict anything but it also won’t contribute to the weight decay.
loss_with_wd = loss + wd * (parameters**2).sum()In fact, we don’t even need to do this because the whole purpose of the loss is to take its gradient. The gradient of parameters squared is 2 times parameters.
parameters.grad += wd * 2 * parametersFold the 2 into the wd since it’s just some number we’re going to pick. When you call fit, pass in the wd parameter:
model = DotProductBias(n_users, n_movies, 50)
learn = Learner(dls, model, loss_func=MSELossFlat())
learn.fit_one_cycle(5, 5e-3, wd=0.1)This finally improves our loss. In fastai applications like vision, fastai sets wd appropriately, but in things like tabular and collaborative filtering fastai doesn’t know enough about your data so you just try a few wd values. Regularization is about making your model no more complex than it has to be. The higher the weights, the more they’re moving the model around, we want to keep the weights down, but not so far down that they don’t make a prediction. If wd is higher, it’ll keep the weights down more, reduce overfitting, but will also reduce the capacity of your model to make good predictions. If it’s lower, it increases the capacity of your model, and increases overfitting.
Can recommendation systems be built based on average ratings of users’ experience rather than collaborative filtering? Not really, if you’ve got lots of metadata you could (demographic data on users for example) then sure averages would be fine. But if all you’ve got is purchasing history, then you really want the granular data, there’s not enough information there to use averages.
Book Notes
Collaborative filtering: look at which products the current user has used or liked, find other users who have used or liked similar products, and then recommend other products that those users have used or liked. We don’t necessarily need to know anything about the products except who liked them.
Latent factors: the key foundational idea in collaborative filtering—the underlying concepts behind users and items that don’t need to be defined explicitly with columns of data.
A First Look at the Data
from fastai.collab import *
from fastai.tabular.all import *
path = untar_data(URLs.ML_100k)ratings = pd.read_csv(path/'u.data', delimiter='\t', header=None, names=['user', 'movie', 'rating', 'timestamp'])
ratings.head()| user | movie | rating | timestamp | |
|---|---|---|---|---|
| 0 | 196 | 242 | 3 | 881250949 |
| 1 | 186 | 302 | 3 | 891717742 |
| 2 | 22 | 377 | 1 | 878887116 |
| 3 | 244 | 51 | 2 | 880606923 |
| 4 | 166 | 346 | 1 | 886397596 |
If we knew for each user to what degree they liked each important category that a movie might fall into, such as genre, age, preferred directors, and actors, and so forth, and we knew the same information about each movie, then a simply way to fill empty ratings would be to multiply this information together for each movie and user combination.
last_skywalker = np.array([0.98, 0.9, -0.9]) # sci-fi, action, old movie
last_skywalkerarray([ 0.98, 0.9 , -0.9 ])user1 = np.array([0.9, 0.8, -0.6]) # sci-fi, action, old movie
user1array([ 0.9, 0.8, -0.6])# combination with 3 being the max
(user1 * last_skywalker).sum()2.1420000000000003dot product: multiplying two vectors together and add up the results.
The mathematical operation of multiplying the elements of two vectors together, and then summing up the results.
casablanca = np.array([-0.99, -0.3, 0.8]) # sci-fi, action, old movie
casablancaarray([-0.99, -0.3 , 0.8 ])# user1 won't like this as much as last skywalker
(user1 * casablanca).sum()-1.611Learning the Latent Factors
There is surprisingly little difference between specifying the structure of a model and learning one, since we can just use our general gradient descent approach:
- Step 1: randomly initialize some parameters.
- Step 2: calculate our predictions.
- Step 3: calculate our loss.
More details:
- Step 1: the parameters we randomly initialize will be a set of latent factors for each user and movie. We’ll use 5 latent factors for now.
- Step 2: calculate predictions by taking the dot product of each movie with each user. If the first latent user factor represents how much the user likes action movies and the first latent movie factor represents whether the movie has a lot of action, the product of those will be particularly high if either the user likes action movies and the movie has a lot of action in it, or the user doesn’t like action movies and the movie doesn’t have any action in it. The product will be low if we have a mismatch.
- Step 3: We’ll pick mean squared error for now.
With this in place we can optimize our parameters using stochastic gradient descent such as to minimize the loss. At each step, the stochastic gradient descent optimizer will calculate the match between each movie and each user using the dot product and will compare it to the actual rating that each user gave to each movie. It will then calculate the derivative of this value and step the weights by multiplying this by the learning rate. After doing this lots of times the loss will get better and the recommendations will also get better and better.
Creating the DataLoaders
To use the Learner.fit function, we will need to get our data into a DataLoaders. When showing the data we would rather see movie titles than their IDs:
movies = pd.read_csv(path/'u.item', delimiter='|', encoding='latin-1', usecols=(0,1), names=('movie', 'title'), header=None)
movies.head()| movie | title | |
|---|---|---|
| 0 | 1 | Toy Story (1995) |
| 1 | 2 | GoldenEye (1995) |
| 2 | 3 | Four Rooms (1995) |
| 3 | 4 | Get Shorty (1995) |
| 4 | 5 | Copycat (1995) |
ratings = ratings.merge(movies)
ratings.head()| user | movie | rating | timestamp | title | |
|---|---|---|---|---|---|
| 0 | 196 | 242 | 3 | 881250949 | Kolya (1996) |
| 1 | 63 | 242 | 3 | 875747190 | Kolya (1996) |
| 2 | 226 | 242 | 5 | 883888671 | Kolya (1996) |
| 3 | 154 | 242 | 3 | 879138235 | Kolya (1996) |
| 4 | 306 | 242 | 5 | 876503793 | Kolya (1996) |
dls = CollabDataLoaders.from_df(ratings, item_name='title', bs=64)
dls.show_batch()| user | title | rating | |
|---|---|---|---|
| 0 | 210 | Some Like It Hot (1959) | 5 |
| 1 | 651 | Godfather, The (1972) | 4 |
| 2 | 515 | Starship Troopers (1997) | 4 |
| 3 | 49 | Swimming with Sharks (1995) | 4 |
| 4 | 512 | Nikita (La Femme Nikita) (1990) | 5 |
| 5 | 497 | Rob Roy (1995) | 4 |
| 6 | 664 | Dave (1993) | 3 |
| 7 | 880 | Empire Strikes Back, The (1980) | 5 |
| 8 | 185 | Leaving Las Vegas (1995) | 4 |
| 9 | 815 | Aladdin (1992) | 3 |
To represent collaborative filtering in PyTorch, we can’t just use the crosstab representation directly, especially if we want to fit into our deep learning framework. We can represent our movie and user latent factor tables as simple matrices:
n_users = len(dls.classes['user'])
n_movies = len(dls.classes['title'])
n_factors = 5
n_users, n_movies, n_factors(944, 1665, 5)user_factors = torch.randn(n_users, n_factors)
movie_factors = torch.randn(n_movies, n_factors)
user_factors.shape, movie_factors.shape(torch.Size([944, 5]), torch.Size([1665, 5]))To calculate the result for a particular movie and user combination, we have to look up the index of the movie in our movie latent factor matrix, and the index of the user in our user latent factor matrix; then we can do our dot product between the two latent factor vectors.
We can represent look up an index as a matrix product by replacing indices with one-hot-encoded vectors.
one_hot_3 = one_hot(3, n_users).float()
user_factors.t() @ one_hot_3tensor([-2.5648, -0.4866, -0.9996, -1.8835, -1.0867])user_factors[3]tensor([-2.5648, -0.4866, -0.9996, -1.8835, -1.0867])If we do that for a few indices at once, we will have a matrix of one-hot-encoded vectors and that operation will be a matrix multiplication. This would be a perfectly acceptable way to build models using this kind of architecture, except that it would use a lot more memory and time than necessary.
one_hot_3tensor([0., 0., 0., 1., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0.,
0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0.,
0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0.,
0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0.,
0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0.,
0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0.,
0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0.,
0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0.,
0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0.,
0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0.,
0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0.,
0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0.,
0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0.,
0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0.,
0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0.,
0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0.,
0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0.,
0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0.,
0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0.,
0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0.,
0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0.,
0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0.,
0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0.,
0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0.,
0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0.,
0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0.,
0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0.,
0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0.,
0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0.,
0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0.,
0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0.,
0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0.,
0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0.,
0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0.,
0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0.,
0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0.,
0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0.,
0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0.,
0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0.,
0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0.,
0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0.,
0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0.,
0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0.,
0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0.,
0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0.,
0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0.,
0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0.,
0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0.,
0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0.,
0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0.,
0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0.,
0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0.,
0., 0., 0., 0., 0., 0., 0., 0.])one_hots = torch.stack([
one_hot(3, n_users).float(),
one_hot(4, n_users).float(),
one_hot(5, n_users).float()])
one_hots @ user_factorstensor([[-2.5648, -0.4866, -0.9996, -1.8835, -1.0867],
[-0.0096, -0.0892, -1.4639, 0.6083, -1.0248],
[ 0.0330, -0.6358, 0.6536, -0.9384, 0.0973]])user_factors[3:6]tensor([[-2.5648, -0.4866, -0.9996, -1.8835, -1.0867],
[-0.0096, -0.0892, -1.4639, 0.6083, -1.0248],
[ 0.0330, -0.6358, 0.6536, -0.9384, 0.0973]])There is no real underlying reason to store the one-hot-encoded vector, or to search through it to find the occurrence of the number 1–we should just be able to index into an array directly with an integer.
embedding: a special layer that indexes into a vector using an integer, but has its derivative calculated in such a way that it is identical to what it would have been if it had done a matrix multiplication with a one-hot-encoded vector.
How do we determine the numbers to characterize these different features of movies and users? We don’t. We let the model learn them. By analyzing the existing relations between users and movies, our model can figure out itself the features that seem important or not.
We will attribute to each of our users and each of our movies a random vector of a certain length (here, n_factors=5), and we will make those learnable parameters. That means that at each step, when we compute the loss by comparing our predictions to our targets, we will compute the gradients of the loss with respect to those embedding vectors and update them with the rules of SGD (or another optimizer).
Collaborative Filtering from Scratch
# example class
class Example:
def __init__(self, a): self.a = a
def say(self, x): return f'Hello {self.a}, {x}.'
Example('Vishal').say('how are you?')'Hello Vishal, how are you?.'Creating a new PyTorch module requires inheriting from Module. When your module is called, PyTorch will call a method in your class called forward and will pass along to that any parameters that are included in the call.
Module??class DotProduct(Module):
def __init__(self, n_users, n_movies, n_factors):
self.user_factors = Embedding(n_users, n_factors)
self.movie_factors = Embedding(n_movies, n_factors)
def forward(self, x):
users = self.user_factors(x[:,0])
movies = self.movie_factors(x[:,1])
return (users * movies).sum(dim=1)x, y = dls.one_batch()
x.shapetorch.Size([64, 2])# doing from scratch so use plain Learner
model = DotProduct(n_users, n_movies, n_factors=50)
learn = Learner(dls, model, loss_func=MSELossFlat())learn.arch--------------------------------------------------------------------------- AttributeError Traceback (most recent call last) <ipython-input-21-57cde8335315> in <cell line: 1>() ----> 1 learn.arch /usr/local/lib/python3.10/dist-packages/fastcore/basics.py in __getattr__(self, k) 494 if self._component_attr_filter(k): 495 attr = getattr(self,self._default,None) --> 496 if attr is not None: return getattr(attr,k) 497 raise AttributeError(k) 498 def __dir__(self): return custom_dir(self,self._dir()) /usr/local/lib/python3.10/dist-packages/torch/nn/modules/module.py in __getattr__(self, name) 1686 if name in modules: 1687 return modules[name] -> 1688 raise AttributeError(f"'{type(self).__name__}' object has no attribute '{name}'") 1689 1690 def __setattr__(self, name: str, value: Union[Tensor, 'Module']) -> None: AttributeError: 'DotProduct' object has no attribute 'arch'
learn.fit_one_cycle(5, 5e-3)| epoch | train_loss | valid_loss | time |
|---|---|---|---|
| 0 | 1.311295 | 1.325218 | 00:11 |
| 1 | 1.011121 | 1.110533 | 00:12 |
| 2 | 0.882769 | 1.013594 | 00:11 |
| 3 | 0.790874 | 0.926204 | 00:12 |
| 4 | 0.769741 | 0.900602 | 00:11 |
Apply sigmoid_range to force predictions to be between 0 and 5:
class DotProduct(Module):
def __init__(self, n_users, n_movies, n_factors, y_range=(0, 5.5)):
self.user_factors = Embedding(n_users, n_factors)
self.movie_factors = Embedding(n_movies, n_factors)
self.y_range = y_range
def forward(self, x):
users = self.user_factors(x[:,0])
movies = self.movie_factors(x[:,1])
return sigmoid_range((users * movies).sum(dim=1), *self.y_range)Before I train, I want to look at why dim=1 is set in sum:
x.shapetorch.Size([64, 2])user_factors = Embedding(n_users, n_factors)
movie_factors = Embedding(n_movies, n_factors)users = user_factors(x[:,0])
movies = movie_factors(x[:,1])users.shape, movies.shape(torch.Size([64, 5]), torch.Size([64, 5]))(users * movies).sum()tensor(-0.0019, grad_fn=<SumBackward0>)(users * movies).sum(dim=1).shapetorch.Size([64])So, dim=1 ensures that the predictions (users * movies) are calculated for each item in the batch.
# doing from scratch so use plain Learner
model = DotProduct(n_users, n_movies, n_factors=50)
learn = Learner(dls, model, loss_func=MSELossFlat())
learn.fit_one_cycle(5, 5e-3)| epoch | train_loss | valid_loss | time |
|---|---|---|---|
| 0 | 0.923018 | 1.000980 | 00:13 |
| 1 | 0.663725 | 0.956221 | 00:13 |
| 2 | 0.439762 | 0.960771 | 00:12 |
| 3 | 0.361286 | 0.964587 | 00:13 |
| 4 | 0.333990 | 0.961902 | 00:14 |
This actually worsened the model!
One obvious missing piece is that some users are just more positive or negative in their recommendations than others, and some movies are just plain better or worse than others. In our current implementation we do not have any way to encode such things. If all you can say about a movie is, for instance, that it is very sci-fi, very action-oriented, and very not old, then you don’t really have any way to say whether most people like it. We can handle this missing piece with biases—a single number for each user and movie that we can add to our score.
class DotProductBias(Module):
def __init__(self, n_users, n_movies, n_factors, y_range=(0,5.5)):
self.user_factors = Embedding(n_users, n_factors)
self.user_bias = Embedding(n_users, 1)
self.movie_factors = Embedding(n_movies, n_factors)
self.movie_bias = Embedding(n_movies, 1)
self.y_range = y_range
def forward(self, x):
users = self.user_factors(x[:,0])
movies = self.movie_factors(x[:,1])
res = (users * movies).sum(dim=1, keepdim=True)
res += self.user_bias(x[:,0]) + self.movie_bias(x[:,1])
return sigmoid_range(res, *self.y_range)Before I train I want to walk through this code to make sure I understand what’s happening at each step and why.
x, y = dls.one_batch()
x.shapetorch.Size([64, 2])user_factors = Embedding(n_users, n_factors)
user_bias = Embedding(n_users, 1)
movie_factors = Embedding(n_movies, n_factors)
movie_bias = Embedding(n_movies, 1)
user_factors, user_bias, movie_factors, movie_bias(Embedding(944, 5), Embedding(944, 1), Embedding(1665, 5), Embedding(1665, 1))users = user_factors(x[:,0])
movies = movie_factors(x[:,1])
users.shape, movies.shape(torch.Size([64, 5]), torch.Size([64, 5]))users[0]tensor([ 0.0005, -0.0128, -0.0086, 0.0043, -0.0140],
grad_fn=<SelectBackward0>)x[0]tensor([ 422, 1407])user_factors(torch.tensor([422]))tensor([[ 0.0005, -0.0128, -0.0086, 0.0043, -0.0140]],
grad_fn=<EmbeddingBackward0>)(users * movies).sum(dim=1, keepdim=True).shape, (users * movies).sum(dim=1, keepdim=False).shape(torch.Size([64, 1]), torch.Size([64]))res = (users * movies).sum(dim=1, keepdim=True)
res += user_bias(x[:,0]) + movie_bias(x[:,1])
res.shapetorch.Size([64, 1])res = (users * movies).sum(dim=1, keepdim=False)
res += user_bias(x[:,0]) + movie_bias(x[:,1])
res.shape--------------------------------------------------------------------------- RuntimeError Traceback (most recent call last) <ipython-input-20-9b69f795397e> in <cell line: 2>() 1 res = (users * movies).sum(dim=1, keepdim=False) ----> 2 res += user_bias(x[:,0]) + movie_bias(x[:,1]) 3 res.shape RuntimeError: output with shape [64] doesn't match the broadcast shape [64, 64]
user_bias(x[:,0]).shapetorch.Size([64, 1])keepdim=True is needed so that we can add the 64 x 1 bias tensors to res.
model = DotProductBias(n_users, n_movies, n_factors=50)
learn = Learner(dls, model, loss_func=MSELossFlat())
learn.fit_one_cycle(5, 5e-3)| epoch | train_loss | valid_loss | time |
|---|---|---|---|
| 0 | 0.838959 | 0.961033 | 00:12 |
| 1 | 0.584438 | 0.919422 | 00:12 |
| 2 | 0.406340 | 0.946146 | 00:13 |
| 3 | 0.323580 | 0.960616 | 00:13 |
| 4 | 0.303791 | 0.959865 | 00:16 |
The valid_loss was decreasing from the first to second epoch but increased from the second to third and third to fourth epoch, which is a sign of overfitting.
Weight Decay
Add the sum of all weights squared to the loss so that when we compute the gradients, it will add a contribution to them that will encourage the weights to be as small as possible.
The larger the coefficients are the sharper the canyons we will have in the loss function. Letting our model learn high parameters might cause it to fit all the data points in the training set with an overcomplex function that has very sharp changes, which will lead to overfitting.
loss_with_wd = loss + wd * (parameters ** 2).sum()
Limiting our weights from growing too much is going to hinder the training of the model, but it will yield a state where it generalizes better.
In practice it would be very inefficient and maybe numerically unstable to compute that big sum and add it to the loss. Adding that sum to the loss function is the same as doing the following to the gradients:
parameters.grad += wd * 2 * parameters
model = DotProductBias(n_users, n_movies, 50)
learn = Learner(dls, model, loss_func=MSELossFlat())
learn.fit_one_cycle(5, 5e-3, wd=0.1)| epoch | train_loss | valid_loss | time |
|---|---|---|---|
| 0 | 0.913064 | 0.965725 | 00:12 |
| 1 | 0.682149 | 0.911183 | 00:12 |
| 2 | 0.539120 | 0.890211 | 00:12 |
| 3 | 0.445476 | 0.877169 | 00:12 |
| 4 | 0.429690 | 0.872437 | 00:12 |
Finally! The loss consistently decreases each epoch.
Creating Our Own Embedding Module
Optimizers require that they can get all the parameters of a module from the module’s parameters method, but this does not happen automatically. If we just add a tensor as an attribute to a Module, it will not be included in parameters:
class T(Module):
def __init__(self): self.a = torch.ones(3)
L(T().parameters())(#0) []To tell Module that we want to treat a tensor as a parameter, we have to wrap it in the nn.Parameter class. This class doesn’t add any functionality (other than automatically calling requires_grad_ for us). It’s used only as a “marker” to show what ot include in parameters.
class T(Module):
def __init__(self): self.a = nn.Parameter(torch.ones(3))
L(T().parameters())(#1) [Parameter containing:
tensor([1., 1., 1.], requires_grad=True)]All PyTorch modules use nn.Parameter for any trainable paramters:
class T(Module):
def __init__(self): self.a = nn.Linear(1, 3, bias=False)
t = T()
L(t.parameters())(#1) [Parameter containing:
tensor([[ 0.7111],
[-0.4145],
[ 0.4969]], requires_grad=True)]type(t.a.weight)torch.nn.parameter.Parameter# create a tensor as a parameter, with random initialization
def create_params(size):
return nn.Parameter(torch.zeros(*size).normal_(0, 0.01))# create DotProductBias without embedding
class DotProductBias2(Module):
def __init__(self, n_users, n_movies, n_factors, y_range=(0, 5.5)):
self.user_factors = create_params([n_users, n_factors])
self.user_bias = create_params([n_users])
self.movie_factors = create_params([n_movies, n_factors])
self.movie_bias = create_params([n_movies])
self.y_range = y_range
def forward(self, x):
users = self.user_factors[x[:,0]]
movies = self.movie_factors[x[:,1]]
res = (users * movies).sum(dim=1)
res += self.user_bias[x[:,0]] + self.movie_bias[x[:,1]]
return sigmoid_range(res, *self.y_range)model = DotProductBias2(n_users, n_movies, 50)
learn = Learner(dls, model, loss_func=MSELossFlat())
learn.fit_one_cycle(5, 5e-3, wd=0.1)| epoch | train_loss | valid_loss | time |
|---|---|---|---|
| 0 | 0.904102 | 0.942020 | 00:11 |
| 1 | 0.654384 | 0.880052 | 00:10 |
| 2 | 0.509761 | 0.857724 | 00:09 |
| 3 | 0.451252 | 0.838781 | 00:10 |
| 4 | 0.445227 | 0.834458 | 00:10 |
x[0]tensor([ 422, 1407])learn.model(x)tensor([3.0069, 2.4127, 3.1486, 3.0827, 4.2363, 3.0727, 4.6257, 2.8603, 4.0537,
2.7821, 1.5680, 3.5075, 1.9389, 4.7167, 3.6408, 2.3103, 3.2855, 3.0170,
4.1721, 4.1315, 4.7459, 4.7006, 3.5047, 3.6348, 2.6413, 2.6047, 4.9137,
3.3948, 3.4747, 3.9256, 3.8448, 3.3731, 3.9032, 1.3075, 4.4401, 3.6986,
3.3045, 3.5697, 4.3211, 3.7295, 1.1871, 3.2220, 3.5667, 3.5309, 4.5825,
2.2819, 4.1466, 3.3740, 4.4830, 3.2561, 3.0671, 3.9423, 2.9384, 4.2050,
2.3258, 4.0698, 4.0947, 2.9023, 3.8935, 3.0650, 3.3615, 3.3382, 3.2790,
4.0849], grad_fn=<AddBackward0>)ratings.head(2)| user | movie | rating | timestamp | title | |
|---|---|---|---|---|---|
| 0 | 196 | 242 | 3 | 881250949 | Kolya (1996) |
| 1 | 63 | 242 | 3 | 875747190 | Kolya (1996) |
learn.get_preds(
dl=learn.dls.test_dl(ratings.head(2), with_input=True, with_decoded=True)
)(tensor([3.9271, 3.7005]),
tensor([[3],
[3]]))learn.get_preds(dl=learn.dls.test_dl(pd.DataFrame(data={'user': [196, 63], 'title': ['Kolya (1996)', 'Kolya (1996)']})))(tensor([3.9271, 3.7005]), None)learn.model(tensor([[ 196, 242]]))tensor([3.1319], grad_fn=<AddBackward0>)Interpreting Embeddings and Biases
The easiest parameters to interpret are biases. For movies with a low bias: even when a user is very well matched to its latent factors (which, as we will see in a moment, tend to represent things like level of action, age of movie, and so forth), they still generally don’t like it.
learn.modelDotProductBias2()learn.model.movie_bias.shapetorch.Size([1665])movie_bias = learn.model.movie_bias.squeeze()
movie_bias.shapetorch.Size([1665])movie_bias[:5]tensor([ 0.0034, -0.1036, 0.0292, -0.0822, 0.4568], grad_fn=<SliceBackward0>)Note: PyTorch’s squeeze:
Returns a tensor with all specified dimensions of input of size 1 removed.
# bottom 5 movies
idxs = movie_bias.argsort()[:5]
[dls.classes['title'][i] for i in idxs]['Children of the Corn: The Gathering (1996)',
'Lawnmower Man 2: Beyond Cyberspace (1996)',
'Solo (1996)',
'Mortal Kombat: Annihilation (1997)',
'Crow: City of Angels, The (1996)']# top 5 movies
idxs = movie_bias.argsort(descending=True)[:5]
[dls.classes['title'][i] for i in idxs]['Shawshank Redemption, The (1994)',
'Good Will Hunting (1997)',
'Titanic (1997)',
"Schindler's List (1993)",
'Rear Window (1954)']learn.model.movie_factors.shapetorch.Size([1665, 50])movie_bias.argsort(descending=True)[:5]tensor([1318, 622, 1501, 1282, 1216])dls.classes['title'][1318]'Shawshank Redemption, The (1994)'PCA code from the fastbook repo:
g = ratings.groupby('title')['rating'].count()
gtitle
'Til There Was You (1997) 9
1-900 (1994) 5
101 Dalmatians (1996) 109
12 Angry Men (1957) 125
187 (1997) 41
...
Young Guns II (1990) 44
Young Poisoner's Handbook, The (1995) 41
Zeus and Roxanne (1997) 6
unknown 9
Á köldum klaka (Cold Fever) (1994) 1
Name: rating, Length: 1664, dtype: int64top_movies = g.sort_values(ascending=False).index.values[:1000]
top_movies[:5]array(['Star Wars (1977)', 'Contact (1997)', 'Fargo (1996)',
'Return of the Jedi (1983)', 'Liar Liar (1997)'], dtype=object)g.sort_values(ascending=False).indexIndex(['Star Wars (1977)', 'Contact (1997)', 'Fargo (1996)',
'Return of the Jedi (1983)', 'Liar Liar (1997)',
'English Patient, The (1996)', 'Scream (1996)', 'Toy Story (1995)',
'Air Force One (1997)', 'Independence Day (ID4) (1996)',
...
'Girl in the Cadillac (1995)', 'He Walked by Night (1948)',
'Hana-bi (1997)', 'Object of My Affection, The (1998)',
'Office Killer (1997)', 'Great Day in Harlem, A (1994)',
'Other Voices, Other Rooms (1997)', 'Good Morning (1971)',
'Girls Town (1996)', 'Á köldum klaka (Cold Fever) (1994)'],
dtype='object', name='title', length=1664)top_idxs = tensor([learn.dls.classes['title'].o2i[m] for m in top_movies])learn.dls.classes['title'].o2i['Star Wars (1977)']1399movie_w = learn.model.movie_factors[top_idxs].cpu().detach()
movie_pca = movie_w.pca(3)
fac0,fac1,fac2 = movie_pca.t()
idxs = list(range(50))
X = fac0[idxs]
Y = fac2[idxs]Using fastai.collab
learn = collab_learner(dls, n_factors=50, y_range=(0, 5.5))
learn.fit_one_cycle(5, 5e-3, wd=0.1)| epoch | train_loss | valid_loss | time |
|---|---|---|---|
| 0 | 0.928530 | 0.946365 | 00:12 |
| 1 | 0.683226 | 0.883067 | 00:10 |
| 2 | 0.506070 | 0.853040 | 00:10 |
| 3 | 0.446197 | 0.840192 | 00:10 |
| 4 | 0.439921 | 0.836284 | 00:10 |
View the names of the model layers
learn.modelEmbeddingDotBias(
(u_weight): Embedding(944, 50)
(i_weight): Embedding(1665, 50)
(u_bias): Embedding(944, 1)
(i_bias): Embedding(1665, 1)
)Replicate previous analyses:
movie_bias = learn.model.i_bias.weight.squeeze()
idxs = movie_bias.argsort(descending=True)[:5]
[dls.classes['title'][i] for i in idxs]['Titanic (1997)',
'Shawshank Redemption, The (1994)',
'Usual Suspects, The (1995)',
"Schindler's List (1993)",
'Silence of the Lambs, The (1991)']g = ratings.groupby('title')['rating'].count()
top_movies = g.sort_values(ascending=False).index.values[:1000]
top_idxs = tensor([learn.dls.classes['title'].o2i[m] for m in top_movies])
movie_w = learn.model.i_weight.weight[top_idxs].cpu().detach()
movie_pca = movie_w.pca(3)
fac0,fac1,fac2 = movie_pca.t()
idxs = list(range(50))
X = fac0[idxs]
Y = fac2[idxs]
plt.figure(figsize=(12,12))
plt.scatter(X, Y)
for i, x, y in zip(top_movies[idxs], X, Y):
plt.text(x,y,i, color=np.random.rand(3)*0.7, fontsize=11)
plt.show()Embedding Distance
If there were two movies that were nearly identical, their embedding vectors would also have to be nearly identical, because the users who would like them would be nearly exactly the same. Movie similarity can be defined by the similarity of users who like those movies. The distance between two movies’ embedding vectors can define that similarity.
# find the most similar movie to Silence of the Lambs
movie_factors = learn.model.i_weight.weight
idx = dls.classes['title'].o2i['Silence of the Lambs, The (1991)']
distances = nn.CosineSimilarity(dim=1)(movie_factors, movie_factors[idx][None])
idx = distances.argsort(descending=True)[1]
dls.classes['title'][idx]'His Girl Friday (1940)'distances.argsort(descending=True)tensor([1330, 688, 846, ..., 1048, 595, 850])Bootstrapping a Collaborative Filtering Model
boostrapping problem: Having no users and therefore no history to learn from. What products do you recommend to your very first user? What do you do when a new user signs up? What do you do when you add a new product to your portfolio? Use your common sense.
- Pick a user to represent average taste (instead of averaging all user embeddings as this can incorrectly represent relationships between latent factors).
- User a tabular model based on user metadata to construct your initial embedding vector. Think about what questions you could ask to help you understand users’ tastes. Create a model with the dependent variable the user’s embedding vector and the independent variables are the rsults of the questions you ask them along with their signup metadata.
- A small number of extremely enthusiastic users may end up effectively setting the recommendations for your whole user base. Such a problem can change the entire makeup of your user base, and the behavior of the system, particularly because of positive feedback loops: a small number of users set the direction of recommendation systems, end up attracting more people like them to your system, amplifyig the original bias, exponentially. Ensure that humans are in the loop of the data pipeline, with careful monitoring of the system and a gradual and thoughtful rollout. Think about all of the ways in which feedback loops may be represented in your system, and how you might be able to identify them in your data.
The dot-product approach to collaborative filtering is known as probabilistic matrix factorization (PMF).
Deep Learning for Collaborative Filtering
Take the results of the embedding lookup and concatenate those activations together, giving us a matrix that we can then pass through linear layers and nonlinearities.
Since we’ll be concatenating the embedding matrices, rather than taking their dot product, the two embedding matrices can have different sizes (different number of latent factors). get_emb_sz returns recommended sizes for embedding matrices based on Jeremy’s intuition for what works well.
embs = get_emb_sz(dls)
embs[(944, 74), (1665, 102)]class CollabNN(Module):
def __init__(self, user_sz, item_sz, y_range=(0, 5.5), n_act=100):
self.user_factors = Embedding(*user_sz)
self.item_factors = Embedding(*item_sz)
self.layers = nn.Sequential(
nn.Linear(user_sz[1]+item_sz[1], n_act),
nn.ReLU(),
nn.Linear(n_act, 1)
)
self.y_range = y_range
def forward(self, x):
embs = self.user_factors(x[:,0]), self.item_factors(x[:,1])
x = self.layers(torch.cat(embs, dim=1))
return sigmoid_range(x, *self.y_range)Working through this code step-by-step:
user_factors = Embedding(*embs[0])
movie_factors = Embedding(*embs[1])
user_factors, movie_factors(Embedding(944, 74), Embedding(1665, 102))layers = nn.Sequential(
nn.Linear(embs[0][1]+embs[1][1], 100),
nn.ReLU(),
nn.Linear(100, 1)
)
layersSequential(
(0): Linear(in_features=176, out_features=100, bias=True)
(1): ReLU()
(2): Linear(in_features=100, out_features=1, bias=True)
)y_range = (0, 5.5)x = dls.one_batch()[0]
x.shapetorch.Size([64, 2])embs = user_factors(x[:,0]), movie_factors(x[:,1])
embs = torch.cat(embs, dim=1)
embs.shapetorch.Size([64, 176])x = layers(embs)
x.shapetorch.Size([64, 1])x = sigmoid_range(x, *y_range)
x.shapetorch.Size([64, 1])# create a model
embs = get_emb_sz(dls)
model = CollabNN(*embs)modelCollabNN(
(user_factors): Embedding(944, 74)
(item_factors): Embedding(1665, 102)
(layers): Sequential(
(0): Linear(in_features=176, out_features=100, bias=True)
(1): ReLU()
(2): Linear(in_features=100, out_features=1, bias=True)
)
)learn = Learner(dls, model, loss_func=MSELossFlat())
learn.fit_one_cycle(5, 5e-3, wd=0.01) # note the smaller wd| epoch | train_loss | valid_loss | time |
|---|---|---|---|
| 0 | 0.909496 | 0.933792 | 00:24 |
| 1 | 0.865688 | 0.909720 | 00:24 |
| 2 | 0.821369 | 0.876649 | 00:23 |
| 3 | 0.772402 | 0.854223 | 00:14 |
| 4 | 0.768974 | 0.850676 | 00:12 |
# alternative way to train a NN
learn = collab_learner(dls, use_nn=True, y_range=(0, 5.5), layers=[100, 50])
learn.fit_one_cycle(5, 5e-3, wd=0.1)| epoch | train_loss | valid_loss | time |
|---|---|---|---|
| 0 | 0.968165 | 0.987966 | 00:18 |
| 1 | 0.906930 | 0.917807 | 00:13 |
| 2 | 0.830938 | 0.884382 | 00:13 |
| 3 | 0.781613 | 0.859800 | 00:13 |
| 4 | 0.749270 | 0.855626 | 00:13 |
fastai uses EmbeddingNN which inherits from TabularModel.
**kwargs in a parameter list means “put any additional keyword arguments into a dict called kwargs.” And **kwargs in an argument list means “insert all key/value pairs in the kwargs dict as named arguments here.”
Jupyter Notebook doesn’t know what parameter are available with **kwargs so things like tab completion or parameter names and pop-up lists won’t work. fastai resolves this by providing a special @delegates decorator which automatically changes the signature of the class or function to insert all of its keyworkd arguments into the signature.
We can incorporate other user and movie information with EmbeddingNN since it uses TabularModel (EmbeddingNN is a TabularModel with n_cont=0 and out_sz=1.)
Questionnaire
1. What problem does colalborative filtering solve?
It solves the problem of “filling in the blanks” to predict which items which users (who haven’t bought those items) will buy or rate highly.
2. How does it solve it?
It solves it buy learning different features (latent factors) of users and items and taking the dot product of a user’s latent factors with an item’s latent factors as the prediction.
3. Why might a collaborative filtering predictive model fail to be a very useful recommendation system?
4. What does a crosstab representation of collaborative filtering data look like?
It looks like a table with rows/columns as users/movies and the cells/values as the rating.
5. Write the code to create a crosstab representation of the MovieLens data.
pd.crosstab(index=ratings['user'], columns=ratings['movie'], values=ratings['rating'], aggfunc='max')| movie | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | ... | 1673 | 1674 | 1675 | 1676 | 1677 | 1678 | 1679 | 1680 | 1681 | 1682 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| user | |||||||||||||||||||||
| 1 | 5.0 | 3.0 | 4.0 | 3.0 | 3.0 | 5.0 | 4.0 | 1.0 | 5.0 | 3.0 | ... | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN |
| 2 | 4.0 | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | 2.0 | ... | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN |
| 3 | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | ... | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN |
| 4 | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | ... | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN |
| 5 | 4.0 | 3.0 | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | ... | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN |
| ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... |
| 939 | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | 5.0 | NaN | ... | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN |
| 940 | NaN | NaN | NaN | 2.0 | NaN | NaN | 4.0 | 5.0 | 3.0 | NaN | ... | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN |
| 941 | 5.0 | NaN | NaN | NaN | NaN | NaN | 4.0 | NaN | NaN | NaN | ... | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN |
| 942 | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | ... | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN |
| 943 | NaN | 5.0 | NaN | NaN | NaN | NaN | NaN | NaN | 3.0 | NaN | ... | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN |
943 rows × 1682 columns
6. What is a latent factor? Why is it “latent”?
A latent factor is some characteristic of a variable such as user or item. It is latent because we do not explicitly know or define it. It is learned through training.
7. What is a dot product? Calculate a dot product manually using pure Python with lists.
A dot product is the sum of elementwise products between two sequences.
a = [0.5, 0.8, 0.6]
b = [0.3, 0.2, 0.1]
dotproduct = 0
for i in range(3):
dotproduct += a[i] * b[i]
dotproduct0.370000000000000058. What does pandas.DataFrame.merge do?
It joins two DataFrames based on a single key column. In our case, we merge ratings with movies to get the title column into ratings.
9. What is an embedding matrix?
A matrix where the rows are users or movies, columns are latent factors, and values are decimal values.
10. What is the relationship between an embedding and a matrix of one-hot-encoded vectors?
An embedding is a lookup for which gradients are calculated for an equivalent one-hot-encoded vector matrix multiplication.
11. Why do we need Embedding if we could use one-hot-encoded vectors for the same thing?
Because one-hot-encoded vectors take up a lot of memory.
12. What does an embedding contain before we start training (assuming we’re not using a pretrained model)?
Random numbers.
13. Create a class (without peeking, if possible!) and use it.
class Example2():
def __init__(self, a): self.a = a
def say(self, text): print(f"Hello {self.a}, {text}")Example2('Vishal').say('how are you doing?')Hello Vishal, how are you doing?14. What does x[:,0] mean?
All rows of the first column.
x = torch.rand((20, 3))
xtensor([[0.9112, 0.0080, 0.1422],
[0.5259, 0.5318, 0.4177],
[0.7601, 0.4428, 0.7609],
[0.1857, 0.6702, 0.5156],
[0.7433, 0.9224, 0.0756],
[0.1144, 0.9052, 0.4352],
[0.2535, 0.6668, 0.5542],
[0.1815, 0.1204, 0.7027],
[0.6851, 0.2904, 0.1381],
[0.4445, 0.2967, 0.3887],
[0.0353, 0.8038, 0.7396],
[0.3166, 0.4250, 0.4495],
[0.8432, 0.9193, 0.0062],
[0.9012, 0.0966, 0.8314],
[0.7679, 0.5781, 0.4155],
[0.4149, 0.3091, 0.3061],
[0.3020, 0.6649, 0.8742],
[0.6168, 0.4744, 0.0328],
[0.9663, 0.3894, 0.5954],
[0.0722, 0.1334, 0.2033]])x[:,0]tensor([0.9112, 0.5259, 0.7601, 0.1857, 0.7433, 0.1144, 0.2535, 0.1815, 0.6851,
0.4445, 0.0353, 0.3166, 0.8432, 0.9012, 0.7679, 0.4149, 0.3020, 0.6168,
0.9663, 0.0722])15. Rewrite the DotProduct class (without peeking, if possible!) and train a model with it.
class DotProduct(Module):
def __init__(self, n_users, n_movies, n_factors):
self.user_factors = Embedding(n_users, n_factors)
self.movie_factors = Embedding(n_movies, n_factors)
def forward(self, x):
users = self.user_factors(x[:,0])
movies = self.movie_factors(x[:,1])
return (users * movies).sum(dim=1)model = DotProduct(n_users, n_movies, n_factors=50)
learn = Learner(dls, model, loss_func=MSELossFlat())
learn.fit_one_cycle(5, 5e-3)| epoch | train_loss | valid_loss | time |
|---|---|---|---|
| 0 | 1.326553 | 1.332127 | 00:11 |
| 1 | 1.056348 | 1.104372 | 00:14 |
| 2 | 0.907263 | 0.994020 | 00:14 |
| 3 | 0.811368 | 0.898383 | 00:11 |
| 4 | 0.746635 | 0.878394 | 00:11 |
16. What is a good loss function to use for MovieLens? Why?
Mean squared error—because we our predictions are continuous values.
17. What would happen if we used cross-entropy loss with MovieLens? How would we need to change the model?
Currently the model predicts a single value—a continuous number for the rating.
model(torch.tensor([[114, 23]]))tensor([2.3010], grad_fn=<SumBackward1>)For Cross-Entropy loss, we need the model to predict 5 probabilities, one for each rating (1, 2, 3, 4, 5). My initial guess for doing this would be to add a linear layer that projects from 1 feature to 5 features.
x,y = dls.one_batch()
x.shapetorch.Size([64, 2])class DotProduct2(Module):
def __init__(self, n_users, n_movies, n_factors):
self.user_factors = Embedding(n_users, n_factors)
self.movie_factors = Embedding(n_movies, n_factors)
self.linear = nn.Linear(1, 5)
def forward(self, x):
users = self.user_factors(x[:,0])
movies = self.movie_factors(x[:,1])
return self.linear((users * movies).sum(dim=1).unsqueeze(0).permute(1,0))model = DotProduct2(n_users, n_movies, n_factors=50)model(x).shapetorch.Size([64, 5])Running this with CollabDataLoaders won’t work because that sets the ratings as a continuous variable. Instead, I need to create a TabularDataLoaders object where the dependent variable y is a categorical ratings column (with vocab being 0, 1, 2, 3 and 4) and then using my updated linear layer model with CrossEntropyLossFlat.
model = DotProduct2(n_users, n_movies, n_factors=50)
learn = Learner(dls, model, loss_func=CrossEntropyLossFlat())
# this won't work
learn.fit_one_cycle(5, 5e-3)| epoch | train_loss | valid_loss | time |
|---|
--------------------------------------------------------------------------- IndexError Traceback (most recent call last) <ipython-input-39-467ada469dfd> in <cell line: 3>() 1 model = DotProduct2(n_users, n_movies, n_factors=50) 2 learn = Learner(dls, model, loss_func=CrossEntropyLossFlat()) ----> 3 learn.fit_one_cycle(5, 5e-3) /usr/local/lib/python3.10/dist-packages/fastai/callback/schedule.py in fit_one_cycle(self, n_epoch, lr_max, div, div_final, pct_start, wd, moms, cbs, reset_opt, start_epoch) 117 scheds = {'lr': combined_cos(pct_start, lr_max/div, lr_max, lr_max/div_final), 118 'mom': combined_cos(pct_start, *(self.moms if moms is None else moms))} --> 119 self.fit(n_epoch, cbs=ParamScheduler(scheds)+L(cbs), reset_opt=reset_opt, wd=wd, start_epoch=start_epoch) 120 121 # %% ../../nbs/14_callback.schedule.ipynb 50 /usr/local/lib/python3.10/dist-packages/fastai/learner.py in fit(self, n_epoch, lr, wd, cbs, reset_opt, start_epoch) 262 self.opt.set_hypers(lr=self.lr if lr is None else lr) 263 self.n_epoch = n_epoch --> 264 self._with_events(self._do_fit, 'fit', CancelFitException, self._end_cleanup) 265 266 def _end_cleanup(self): self.dl,self.xb,self.yb,self.pred,self.loss = None,(None,),(None,),None,None /usr/local/lib/python3.10/dist-packages/fastai/learner.py in _with_events(self, f, event_type, ex, final) 197 198 def _with_events(self, f, event_type, ex, final=noop): --> 199 try: self(f'before_{event_type}'); f() 200 except ex: self(f'after_cancel_{event_type}') 201 self(f'after_{event_type}'); final() /usr/local/lib/python3.10/dist-packages/fastai/learner.py in _do_fit(self) 251 for epoch in range(self.n_epoch): 252 self.epoch=epoch --> 253 self._with_events(self._do_epoch, 'epoch', CancelEpochException) 254 255 def fit(self, n_epoch, lr=None, wd=None, cbs=None, reset_opt=False, start_epoch=0): /usr/local/lib/python3.10/dist-packages/fastai/learner.py in _with_events(self, f, event_type, ex, final) 197 198 def _with_events(self, f, event_type, ex, final=noop): --> 199 try: self(f'before_{event_type}'); f() 200 except ex: self(f'after_cancel_{event_type}') 201 self(f'after_{event_type}'); final() /usr/local/lib/python3.10/dist-packages/fastai/learner.py in _do_epoch(self) 245 246 def _do_epoch(self): --> 247 self._do_epoch_train() 248 self._do_epoch_validate() 249 /usr/local/lib/python3.10/dist-packages/fastai/learner.py in _do_epoch_train(self) 237 def _do_epoch_train(self): 238 self.dl = self.dls.train --> 239 self._with_events(self.all_batches, 'train', CancelTrainException) 240 241 def _do_epoch_validate(self, ds_idx=1, dl=None): /usr/local/lib/python3.10/dist-packages/fastai/learner.py in _with_events(self, f, event_type, ex, final) 197 198 def _with_events(self, f, event_type, ex, final=noop): --> 199 try: self(f'before_{event_type}'); f() 200 except ex: self(f'after_cancel_{event_type}') 201 self(f'after_{event_type}'); final() /usr/local/lib/python3.10/dist-packages/fastai/learner.py in all_batches(self) 203 def all_batches(self): 204 self.n_iter = len(self.dl) --> 205 for o in enumerate(self.dl): self.one_batch(*o) 206 207 def _backward(self): self.loss_grad.backward() /usr/local/lib/python3.10/dist-packages/fastai/learner.py in one_batch(self, i, b) 233 b = self._set_device(b) 234 self._split(b) --> 235 self._with_events(self._do_one_batch, 'batch', CancelBatchException) 236 237 def _do_epoch_train(self): /usr/local/lib/python3.10/dist-packages/fastai/learner.py in _with_events(self, f, event_type, ex, final) 197 198 def _with_events(self, f, event_type, ex, final=noop): --> 199 try: self(f'before_{event_type}'); f() 200 except ex: self(f'after_cancel_{event_type}') 201 self(f'after_{event_type}'); final() /usr/local/lib/python3.10/dist-packages/fastai/learner.py in _do_one_batch(self) 217 self('after_pred') 218 if len(self.yb): --> 219 self.loss_grad = self.loss_func(self.pred, *self.yb) 220 self.loss = self.loss_grad.clone() 221 self('after_loss') /usr/local/lib/python3.10/dist-packages/fastai/losses.py in __call__(self, inp, targ, **kwargs) 52 if targ.dtype in [torch.int8, torch.int16, torch.int32]: targ = targ.long() 53 if self.flatten: inp = inp.view(-1,inp.shape[-1]) if self.is_2d else inp.view(-1) ---> 54 return self.func.__call__(inp, targ.view(-1) if self.flatten else targ, **kwargs) 55 56 def to(self, device:torch.device): /usr/local/lib/python3.10/dist-packages/torch/nn/modules/module.py in _wrapped_call_impl(self, *args, **kwargs) 1509 return self._compiled_call_impl(*args, **kwargs) # type: ignore[misc] 1510 else: -> 1511 return self._call_impl(*args, **kwargs) 1512 1513 def _call_impl(self, *args, **kwargs): /usr/local/lib/python3.10/dist-packages/torch/nn/modules/module.py in _call_impl(self, *args, **kwargs) 1518 or _global_backward_pre_hooks or _global_backward_hooks 1519 or _global_forward_hooks or _global_forward_pre_hooks): -> 1520 return forward_call(*args, **kwargs) 1521 1522 try: /usr/local/lib/python3.10/dist-packages/torch/nn/modules/loss.py in forward(self, input, target) 1177 1178 def forward(self, input: Tensor, target: Tensor) -> Tensor: -> 1179 return F.cross_entropy(input, target, weight=self.weight, 1180 ignore_index=self.ignore_index, reduction=self.reduction, 1181 label_smoothing=self.label_smoothing) /usr/local/lib/python3.10/dist-packages/torch/nn/functional.py in cross_entropy(input, target, weight, size_average, ignore_index, reduce, reduction, label_smoothing) 3043 """ 3044 if has_torch_function_variadic(input, target, weight): -> 3045 return handle_torch_function( 3046 cross_entropy, 3047 (input, target, weight), /usr/local/lib/python3.10/dist-packages/torch/overrides.py in handle_torch_function(public_api, relevant_args, *args, **kwargs) 1619 # Use `public_api` instead of `implementation` so __torch_function__ 1620 # implementations can do equality/identity comparisons. -> 1621 result = torch_func_method(public_api, types, args, kwargs) 1622 1623 if result is not NotImplemented: /usr/local/lib/python3.10/dist-packages/fastai/torch_core.py in __torch_function__(cls, func, types, args, kwargs) 380 if cls.debug and func.__name__ not in ('__str__','__repr__'): print(func, types, args, kwargs) 381 if _torch_handled(args, cls._opt, func): types = (torch.Tensor,) --> 382 res = super().__torch_function__(func, types, args, ifnone(kwargs, {})) 383 dict_objs = _find_args(args) if args else _find_args(list(kwargs.values())) 384 if issubclass(type(res),TensorBase) and dict_objs: res.set_meta(dict_objs[0],as_copy=True) /usr/local/lib/python3.10/dist-packages/torch/_tensor.py in __torch_function__(cls, func, types, args, kwargs) 1416 1417 with _C.DisableTorchFunctionSubclass(): -> 1418 ret = func(*args, **kwargs) 1419 if func in get_default_nowrap_functions(): 1420 return ret /usr/local/lib/python3.10/dist-packages/torch/nn/functional.py in cross_entropy(input, target, weight, size_average, ignore_index, reduce, reduction, label_smoothing) 3057 if size_average is not None or reduce is not None: 3058 reduction = _Reduction.legacy_get_string(size_average, reduce) -> 3059 return torch._C._nn.cross_entropy_loss(input, target, weight, _Reduction.get_enum(reduction), ignore_index, label_smoothing) 3060 3061 IndexError: Target 5 is out of bounds.
ratings[['user', 'title', 'rating']].head()| user | title | rating | |
|---|---|---|---|
| 0 | 196 | Kolya (1996) | 3 |
| 1 | 63 | Kolya (1996) | 3 |
| 2 | 226 | Kolya (1996) | 5 |
| 3 | 154 | Kolya (1996) | 3 |
| 4 | 306 | Kolya (1996) | 5 |
dls = TabularDataLoaders.from_df(
ratings[['user', 'title', 'rating']],
procs=[Categorify],
cat_names=['user','title'],
y_names=['rating'],
y_block=CategoryBlock)dls.vocab[1, 2, 3, 4, 5]b = dls.one_batch()b[0].shape, b[1].shape, b[2].shape(torch.Size([64, 2]), torch.Size([64, 0]), torch.Size([64, 1]))Since the TabularDataLoaders is going to pass categorical and continuous (empty) values to the model, I’ll have to update the model’s forward pass accordingly.
class DotProduct3(Module):
def __init__(self, n_users, n_movies, n_factors):
self.user_factors = Embedding(n_users, n_factors)
self.movie_factors = Embedding(n_movies, n_factors)
self.linear = nn.Linear(1, 5)
def forward(self, x_cat, x_cont):
x = x_cat
users = self.user_factors(x[:,0])
movies = self.movie_factors(x[:,1])
return self.linear((users * movies).sum(dim=1).unsqueeze(0).permute(1,0))model = DotProduct3(n_users, n_movies, n_factors=50)
learn = Learner(dls, model, loss_func=CrossEntropyLossFlat(), metrics=accuracy)
learn.fit_one_cycle(5, 5e-3)| epoch | train_loss | valid_loss | accuracy | time |
|---|---|---|---|---|
| 0 | 1.365067 | 1.474111 | 0.344700 | 00:35 |
| 1 | 1.181627 | 1.604257 | 0.351150 | 00:15 |
| 2 | 1.017730 | 1.770345 | 0.358350 | 00:16 |
| 3 | 0.942282 | 1.899246 | 0.360700 | 00:21 |
| 4 | 0.902040 | 1.926463 | 0.359450 | 00:25 |
It’s not a great model, but it works! To recap, the three changes I made:
- Project the dot product to 5 values using a
nn.Linearlayer. - Use
TabularDataLoadersinstead ofCollabDataLoaders. - Use
CrossEntropyLossFlatinstead ofMSELossFlat.
18. What is the use of bias in the dot product model?
If you take away user preferences and movie characteristics, the bias represents how good or bad a movie is. It’s like a baseline rating sans preference. Low bias = bad movie even if it matches your preferences, high bias = good movie regardless of your preference.
19. What is another name for weight decay?
L2 regularization.
20. Write the equation for weight decay (without peeking!)
loss_with_wd = loss + wd * parameters.sum() ** 2
21. Write the equation for the gradient of weight decay. Why does it help reduce weights?
params.grad += 2 * wd * parameters.sum()
Increasing the loss by the weighted sum of parameters causes the parameters to reduce since the model is trying to minimize the loss and therefore minimize the sum of the parameters (weights).
22. Why does reducing weights lead to better generalization?
Because lower weights result in smoother surfaces where the model won’t overfit to data as it does if weights are higher and the surface is full of sharp peaks and valleys.
23. What does argsort do in PyTorch?
Return the indexes of the current values in the tensor in sorted order.
t = torch.tensor([1, 4, 3, 2])
t.argsort()tensor([0, 3, 2, 1])24. Does sorting the movie biases give the same result as averaging overall movie ratings by movie? Why/why not?
learn = collab_learner(dls, n_factors=50, y_range=(0, 5.5))
learn.fit_one_cycle(5, 5e-3, wd=0.1)| epoch | train_loss | valid_loss | time |
|---|---|---|---|
| 0 | 0.894813 | 0.955763 | 00:21 |
| 1 | 0.693337 | 0.897217 | 00:15 |
| 2 | 0.512773 | 0.869337 | 00:13 |
| 3 | 0.448445 | 0.854036 | 00:11 |
| 4 | 0.438284 | 0.849818 | 00:10 |
movie_bias = learn.model.i_bias.weight.squeeze()
idxs = movie_bias.argsort(descending=True)[:5]
[dls.classes['title'][i] for i in idxs]["Schindler's List (1993)",
'Good Will Hunting (1997)',
'Titanic (1997)',
'Shawshank Redemption, The (1994)',
'Silence of the Lambs, The (1991)']ratings.groupby('title')['rating'].mean().sort_values(ascending=False)title
They Made Me a Criminal (1939) 5.0
Marlene Dietrich: Shadow and Light (1996) 5.0
Saint of Fort Washington, The (1993) 5.0
Someone Else's America (1995) 5.0
Star Kid (1997) 5.0
...
Eye of Vichy, The (Oeil de Vichy, L') (1993) 1.0
King of New York (1990) 1.0
Touki Bouki (Journey of the Hyena) (1973) 1.0
Bloody Child, The (1996) 1.0
Crude Oasis, The (1995) 1.0
Name: rating, Length: 1664, dtype: float64No, as shown above sorting movie biases doesn’t give the same result as sorting by average movie rating. The reason is that the full rating takes into account different movie and user characteristics, while the bias does not.
25. How do you print the names and details of the layers in a model?
By running a cell with the model list so:
learn.modelEmbeddingDotBias(
(u_weight): Embedding(944, 50)
(i_weight): Embedding(1665, 50)
(u_bias): Embedding(944, 1)
(i_bias): Embedding(1665, 1)
)26. What is the “bootstrapping problem” in collaborative filtering?
Dealing with new movies or new users that you don’t have information on.
27. How could you deal with the bootstrapping problem for new users? For new movies?
For new users, you can find the “average user” or use a TabularModel to predict the embeddings for this user. For new movies you can do the same. You can also collect metadata about the movies and users and use that in your model as additional information to train on.
28. How can feedback loops impact collaborative filtering systems?
A small number of users who are using and/or rating a lot of products will skew the recommendation system towards their latent factors, recommending products they like to its users and thus attracting more users that like those narrow band of products. The platform will thus become focused on this narrow band of products and users.
29. When using a neural network in collaborative filtering, why can we have different numbers of factors for movies and users?
Because we eventually will concatenate them before passing them through (matrix multiplying by) the first Linear Layer.
30. Why is there an nn.Sequential in the CollabNN model?
Because that is the Neural Net (NN).
31. What kind of model should we use if we want to add metadata about users and items, or information such as date and time, to a collaborative filtering system?
Tabular.
Further Research
Take a look at all the differences between the
Embeddingversion ofDotProductBiasand thecreate_paramsversion and try to understand why each of those changes is required. If you’re not sure, try reverting each change to see what happens. Even the type of brackets used inforwardhas changed?Find three other areas where collaborative filtering is being used, and identify the pros and cons of this approach in those areas.
Complete this notebook using the full MovieLens dataset, and compare your results to online benchmarks. See if you can improve your accuracy. Look on the book’s website and the fast.ai forums for ideas. Note that there are more columns in the full dataset–see if you can use those too (the next chapter might give you ideas).
Create a model for MovieLens that works with cross-entropy loss, and compare it to the model in this chapter.
Label Smoothing Cross Entropy Loss
I’ll work through the example in Aman Arora’s blog post in which he implements Label Smoothing Cross Entropy Loss.
# logits
X = torch.tensor([
[4.2, -2.4],
[1.6, -0.6],
[3.6, 1.2],
[-0.5, 0.5],
[-0.25, 1.7]
])
# labels
y = torch.tensor([0,1,1,0,0])
X, y(tensor([[ 4.2000, -2.4000],
[ 1.6000, -0.6000],
[ 3.6000, 1.2000],
[-0.5000, 0.5000],
[-0.2500, 1.7000]]),
tensor([0, 1, 1, 0, 0]))LabelSmoothingCrossEntropy(eps=0.1, reduction='none')(X,y) # matches Excel calculationstensor([0.3314, 2.1951, 2.3668, 1.2633, 1.9855])noisy_y = tensor([[0.95, 0.05], [0.05, 0.95], [0.05, 0.95], [0.95, 0.05], [0.95, 0.05]])
noisy_ytensor([[0.9500, 0.0500],
[0.0500, 0.9500],
[0.0500, 0.9500],
[0.9500, 0.0500],
[0.9500, 0.0500]])c = X.size()[-1]
c # number of classes2# with mean reduction
log_preds = F.log_softmax(X, dim=-1)
loss = reduce_loss(-log_preds.sum(dim=-1), 'mean')
nll = F.nll_loss(log_preds, y, reduction='mean')
(1-0.1)*nll + 0.1*(loss/c)tensor(1.6284)# without reduction
log_preds = F.log_softmax(X, dim=-1)
loss = reduce_loss(-log_preds.sum(dim=-1), 'none')
nll = F.nll_loss(log_preds, y, reduction='none')
(1-0.1)*nll + 0.1*(loss/c) # matches Excel calculationstensor([0.3314, 2.1951, 2.3668, 1.2633, 1.9855])((1-0.1)*nll + 0.1*(loss/c)).mean() # same as w/ mean reductiontensor(1.6284)loss # this is the negative sum of log_preds for both classestensor([6.6027, 2.4102, 2.5737, 1.6265, 2.2160])-log_preds.sum(dim=-1) * 0.1 /2 # epsilon weighted negative sum of log_preds for both classestensor([0.3301, 0.1205, 0.1287, 0.0813, 0.1108])nll * 0.9 # epsilon of negative log loss of target classestensor([1.2235e-03, 2.0746e+00, 2.2382e+00, 1.1819e+00, 1.8747e+00])0.9 * nll + -log_preds.sum(dim=-1) * 0.1 /2 # matches Excel calculationstensor([0.3314, 2.1951, 2.3668, 1.2633, 1.9855])Xtensor([[ 4.2000, -2.4000],
[ 1.6000, -0.6000],
[ 3.6000, 1.2000],
[-0.5000, 0.5000],
[-0.2500, 1.7000]])(-torch.log(F.softmax(X, dim=-1)) * noisy_y).sum(dim=-1) # matches Excel calculationstensor([0.3314, 2.1951, 2.3668, 1.2633, 1.9855])nlltensor([1.3595e-03, 2.3051e+00, 2.4868e+00, 1.3133e+00, 2.0830e+00])-torch.log(F.softmax(X, dim=-1)) # notice that nll is the loss values of the target classtensor([[1.3595e-03, 6.6014e+00],
[1.0508e-01, 2.3051e+00],
[8.6836e-02, 2.4868e+00],
[1.3133e+00, 3.1326e-01],
[2.0830e+00, 1.3302e-01]])-log_preds # same as -torch.log(F.softmax(X,dim=-1))tensor([[1.3595e-03, 6.6014e+00],
[1.0508e-01, 2.3051e+00],
[8.6836e-02, 2.4868e+00],
[1.3133e+00, 3.1326e-01],
[2.0830e+00, 1.3302e-01]])-log_preds.sum(dim=-1) # same as `loss`tensor([6.6027, 2.4102, 2.5737, 1.6265, 2.2160])So I think what’s going on here is that nll is just the chosen label’s probabilities whereas loss is the sum of both label’s probs. So multiplying nll by 0.1 and then adding 0.05 * loss results in the ground truth being multiplies by 0.95 (0.9 + 0.05) and not-truth being multiplied by 0.05. I think.
Lesson 8: Convolutions
THE FINAL LESSON OF PART 1!!!!
Video Notes
Before you dig into this, make sure you understand the Linear model and neural net from scratch notebook. I’ll start by walking through that code first:
from pathlib import Path
cred_path = Path("~/.kaggle/kaggle.json").expanduser()
if not cred_path.exists():
cred_path.parent.mkdir(exist_ok=True)
cred_path.write_text(creds)
cred_path.chmod(0o600)path = Path('titanic')
if not path.exists():
import zipfile,kaggle
kaggle.api.competition_download_cli(str(path))
zipfile.ZipFile(f'{path}.zip').extractall(path)Downloading titanic.zip to /content100%|██████████| 34.1k/34.1k [00:00<00:00, 15.2MB/s]path = Path('/content/titanic')import torch, numpy as np, pandas as pd
np.set_printoptions(linewidth=140)
torch.set_printoptions(linewidth=140, sci_mode=False, edgeitems=7)
pd.set_option('display.width', 140)df = pd.read_csv(path/'train.csv')
df| PassengerId | Survived | Pclass | Name | Sex | Age | SibSp | Parch | Ticket | Fare | Cabin | Embarked | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 1 | 0 | 3 | Braund, Mr. Owen Harris | male | 22.0 | 1 | 0 | A/5 21171 | 7.2500 | NaN | S |
| 1 | 2 | 1 | 1 | Cumings, Mrs. John Bradley (Florence Briggs Th... | female | 38.0 | 1 | 0 | PC 17599 | 71.2833 | C85 | C |
| 2 | 3 | 1 | 3 | Heikkinen, Miss. Laina | female | 26.0 | 0 | 0 | STON/O2. 3101282 | 7.9250 | NaN | S |
| 3 | 4 | 1 | 1 | Futrelle, Mrs. Jacques Heath (Lily May Peel) | female | 35.0 | 1 | 0 | 113803 | 53.1000 | C123 | S |
| 4 | 5 | 0 | 3 | Allen, Mr. William Henry | male | 35.0 | 0 | 0 | 373450 | 8.0500 | NaN | S |
| ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... |
| 886 | 887 | 0 | 2 | Montvila, Rev. Juozas | male | 27.0 | 0 | 0 | 211536 | 13.0000 | NaN | S |
| 887 | 888 | 1 | 1 | Graham, Miss. Margaret Edith | female | 19.0 | 0 | 0 | 112053 | 30.0000 | B42 | S |
| 888 | 889 | 0 | 3 | Johnston, Miss. Catherine Helen "Carrie" | female | NaN | 1 | 2 | W./C. 6607 | 23.4500 | NaN | S |
| 889 | 890 | 1 | 1 | Behr, Mr. Karl Howell | male | 26.0 | 0 | 0 | 111369 | 30.0000 | C148 | C |
| 890 | 891 | 0 | 3 | Dooley, Mr. Patrick | male | 32.0 | 0 | 0 | 370376 | 7.7500 | NaN | Q |
891 rows × 12 columns
df.isna().sum()PassengerId 0
Survived 0
Pclass 0
Name 0
Sex 0
Age 177
SibSp 0
Parch 0
Ticket 0
Fare 0
Cabin 687
Embarked 2
dtype: int64# replacce missing values with mode
modes = df.mode().iloc[0]
modesPassengerId 1
Survived 0.0
Pclass 3.0
Name Abbing, Mr. Anthony
Sex male
Age 24.0
SibSp 0.0
Parch 0.0
Ticket 1601
Fare 8.05
Cabin B96 B98
Embarked S
Name: 0, dtype: objectdf.fillna(modes, inplace=True)df.isna().sum().sum()0import numpy as np
df.describe(include=(np.number))| PassengerId | Survived | Pclass | Age | SibSp | Parch | Fare | |
|---|---|---|---|---|---|---|---|
| count | 891.000000 | 891.000000 | 891.000000 | 891.000000 | 891.000000 | 891.000000 | 891.000000 |
| mean | 446.000000 | 0.383838 | 2.308642 | 28.566970 | 0.523008 | 0.381594 | 32.204208 |
| std | 257.353842 | 0.486592 | 0.836071 | 13.199572 | 1.102743 | 0.806057 | 49.693429 |
| min | 1.000000 | 0.000000 | 1.000000 | 0.420000 | 0.000000 | 0.000000 | 0.000000 |
| 25% | 223.500000 | 0.000000 | 2.000000 | 22.000000 | 0.000000 | 0.000000 | 7.910400 |
| 50% | 446.000000 | 0.000000 | 3.000000 | 24.000000 | 0.000000 | 0.000000 | 14.454200 |
| 75% | 668.500000 | 1.000000 | 3.000000 | 35.000000 | 1.000000 | 0.000000 | 31.000000 |
| max | 891.000000 | 1.000000 | 3.000000 | 80.000000 | 8.000000 | 6.000000 | 512.329200 |
# normalize the values with log
df['LogFare'] = np.log(df['Fare']+1)# summary of non-numeric columns
df.describe(include=[object])| Name | Sex | Ticket | Cabin | Embarked | |
|---|---|---|---|---|---|
| count | 891 | 891 | 891 | 891 | 891 |
| unique | 891 | 2 | 681 | 147 | 3 |
| top | Braund, Mr. Owen Harris | male | 347082 | B96 B98 | S |
| freq | 1 | 577 | 7 | 691 | 646 |
# create dummy variables for categorical columns with low cardinality
df = pd.get_dummies(df, columns=["Sex","Pclass","Embarked"], dtype=float)
df.columnsIndex(['PassengerId', 'Survived', 'Name', 'Age', 'SibSp', 'Parch', 'Ticket', 'Fare', 'Cabin', 'LogFare', 'Sex_female', 'Sex_male',
'Pclass_1', 'Pclass_2', 'Pclass_3', 'Embarked_C', 'Embarked_Q', 'Embarked_S'],
dtype='object')added_cols = ['Sex_male', 'Sex_female', 'Pclass_1', 'Pclass_2', 'Pclass_3', 'Embarked_C', 'Embarked_Q', 'Embarked_S']
df[added_cols].head()| Sex_male | Sex_female | Pclass_1 | Pclass_2 | Pclass_3 | Embarked_C | Embarked_Q | Embarked_S | |
|---|---|---|---|---|---|---|---|---|
| 0 | 1.0 | 0.0 | 0.0 | 0.0 | 1.0 | 0.0 | 0.0 | 1.0 |
| 1 | 0.0 | 1.0 | 1.0 | 0.0 | 0.0 | 1.0 | 0.0 | 0.0 |
| 2 | 0.0 | 1.0 | 0.0 | 0.0 | 1.0 | 0.0 | 0.0 | 1.0 |
| 3 | 0.0 | 1.0 | 1.0 | 0.0 | 0.0 | 0.0 | 0.0 | 1.0 |
| 4 | 1.0 | 0.0 | 0.0 | 0.0 | 1.0 | 0.0 | 0.0 | 1.0 |
# create independent and dependent variables as tensors
from torch import tensor
t_dep = tensor(df.Survived)
t_dep[:10]tensor([0, 1, 1, 1, 0, 0, 0, 0, 1, 1])df[added_cols].dtypesSex_male float64
Sex_female float64
Pclass_1 float64
Pclass_2 float64
Pclass_3 float64
Embarked_C float64
Embarked_Q float64
Embarked_S float64
dtype: objectindep_cols = ['Age', 'SibSp', 'Parch', 'LogFare'] + added_cols
t_indep = tensor(df[indep_cols].values, dtype=torch.float)
t_indep.shapetorch.Size([891, 12])torch.manual_seed(442)
n_coeff = t_indep.shape[1]
n_coeff12coeffs = torch.rand(n_coeff)-0.5
coeffs.shapetorch.Size([12])coeffs[:10]tensor([-0.4629, 0.1386, 0.2409, -0.2262, -0.2632, -0.3147, 0.4876, 0.3136, 0.2799, -0.4392])Our predictions will be calculated by multiplying each row by the coefficients, and adding them up.
# each row has 12 variables, one coefficient per variable
# the coefficients are broadcasted to each row
(t_indep*coeffs).shapetorch.Size([891, 12])(t_indep*coeffs)[:2]tensor([[-10.1838, 0.1386, 0.0000, -0.4772, -0.2632, -0.0000, 0.0000, 0.0000, 0.2799, -0.0000, 0.0000, 0.3625],
[-17.5902, 0.1386, 0.0000, -0.9681, -0.0000, -0.3147, 0.4876, 0.0000, 0.0000, -0.4392, 0.0000, 0.0000]])# normal so age doesn't dominate the values when summing the predictions
t_indep.max(), t_indep.max(dim=0)(tensor(80.),
torch.return_types.max(
values=tensor([80.0000, 8.0000, 6.0000, 6.2409, 1.0000, 1.0000, 1.0000, 1.0000, 1.0000, 1.0000, 1.0000, 1.0000]),
indices=tensor([630, 159, 678, 258, 0, 1, 1, 9, 0, 1, 5, 0])))vals, indices = t_indep.max(dim=0)
# division by vals broadcasted to each row
t_indep = t_indep / vals
t_indep[:2]tensor([[0.2750, 0.1250, 0.0000, 0.3381, 1.0000, 0.0000, 0.0000, 0.0000, 1.0000, 0.0000, 0.0000, 1.0000],
[0.4750, 0.1250, 0.0000, 0.6859, 0.0000, 1.0000, 1.0000, 0.0000, 0.0000, 1.0000, 0.0000, 0.0000]])(t_indep*coeffs)[:2]tensor([[-0.1273, 0.0173, 0.0000, -0.0765, -0.2632, -0.0000, 0.0000, 0.0000, 0.2799, -0.0000, 0.0000, 0.3625],
[-0.2199, 0.0173, 0.0000, -0.1551, -0.0000, -0.3147, 0.4876, 0.0000, 0.0000, -0.4392, 0.0000, 0.0000]])(t_indep*coeffs).sum()tensor(5.1269)preds = (t_indep*coeffs).sum(axis=1)
preds.shapetorch.Size([891])# loss function
torch.abs(preds-t_dep).mean()tensor(0.5382)(preds-t_dep)[:5]tensor([ 0.1927, -1.6239, -0.9021, -0.7944, 0.0968])# create helper functions
def calc_preds(coeffs, indeps): return (indeps*coeffs).sum(axis=1)
def calc_loss(coeffs, indeps, deps): return torch.abs(calc_preds(coeffs, indeps)-deps).mean()(calc_preds(coeffs, t_indep) == (coeffs*t_indep).sum(axis=1)).sum()tensor(891)calc_loss(coeffs, t_indep, t_dep) == torch.abs(preds-t_dep).mean()tensor(True)# prepare for gradient descent
coeffs.requires_grad_()tensor([-0.4629, 0.1386, 0.2409, -0.2262, -0.2632, -0.3147, 0.4876, 0.3136, 0.2799, -0.4392, 0.2103, 0.3625], requires_grad=True)loss = calc_loss(coeffs, t_indep, t_dep)
losstensor(0.5382, grad_fn=<MeanBackward0>)# calculate gradients
loss.backward()coeffs.gradtensor([-0.0106, 0.0129, -0.0041, -0.0484, 0.2099, -0.2132, -0.1212, -0.0247, 0.1425, -0.1886, -0.0191, 0.2043])# gradients added when calling backward
loss = calc_loss(coeffs, t_indep, t_dep)
loss.backward()
coeffs.gradtensor([-0.0212, 0.0258, -0.0082, -0.0969, 0.4198, -0.4265, -0.2424, -0.0494, 0.2851, -0.3771, -0.0382, 0.4085])losstensor(0.5382, grad_fn=<MeanBackward0>)# do a gradient descent step
loss = calc_loss(coeffs, t_indep, t_dep)
loss.backward()
with torch.no_grad():
coeffs.sub_(coeffs.grad * 0.1) # update the parameters (coefficients)
coeffs.grad.zero_() # set gradients of coefficients to 0
print(calc_loss(coeffs, t_indep, t_dep)) # yay the loss decreasedtensor(0.4945)from fastai.data.transforms import RandomSplitter
trn_split,val_split=RandomSplitter(seed=42)(df)len(trn_split), len(val_split), trn_split[:5], val_split[:5](713, 178, (#5) [788,525,821,253,374], (#5) [303,778,531,385,134])trn_indep,val_indep = t_indep[trn_split],t_indep[val_split]
trn_dep,val_dep = t_dep[trn_split],t_dep[val_split]
len(trn_indep),len(val_indep)(713, 178)def update_coeffs(coeffs, lr):
coeffs.sub_(coeffs.grad * lr)
coeffs.grad.zero_()def one_epoch(coeffs, lr):
loss = calc_loss(coeffs, trn_indep, trn_dep)
loss.backward()
with torch.no_grad(): update_coeffs(coeffs, lr)
print(f"{loss:.3f}", end="; ")def init_coeffs(): return (torch.rand(n_coeff)-0.5).requires_grad_()def train_model(epochs=30, lr=0.01):
torch.manual_seed(442)
coeffs = init_coeffs()
for i in range(epochs): one_epoch(coeffs, lr=lr)
return coeffscoeffs = train_model(18, lr=0.2)0.536; 0.502; 0.477; 0.454; 0.431; 0.409; 0.388; 0.367; 0.349; 0.336; 0.330; 0.326; 0.329; 0.304; 0.314; 0.296; 0.300; 0.289; def show_coeffs(): return dict(zip(indep_cols, coeffs.requires_grad_(False)))
show_coeffs(){'Age': tensor(-0.2694),
'SibSp': tensor(0.0901),
'Parch': tensor(0.2359),
'LogFare': tensor(0.0280),
'Sex_male': tensor(-0.3990),
'Sex_female': tensor(0.2345),
'Pclass_1': tensor(0.7232),
'Pclass_2': tensor(0.4112),
'Pclass_3': tensor(0.3601),
'Embarked_C': tensor(0.0955),
'Embarked_Q': tensor(0.2395),
'Embarked_S': tensor(0.2122)}preds = calc_preds(coeffs, val_indep)results = val_dep.bool()==(preds>0.5)
results[:16]tensor([ True, True, True, True, True, True, True, True, True, True, False, False, False, True, True, False])results.float().mean()tensor(0.7865)def acc(coeffs): return (val_dep.bool()==(calc_preds(coeffs, val_indep)>0.5)).float().mean()
acc(coeffs)tensor(0.7865)preds[:28]tensor([ 0.8160, 0.1295, -0.0148, 0.1831, 0.1520, 0.1350, 0.7279, 0.7754, 0.3222, 0.6740, 0.0753, 0.0389, 0.2216, 0.7631,
0.0678, 0.3997, 0.3324, 0.8278, 0.1078, 0.7126, 0.1023, 0.3627, 0.9937, 0.8050, 0.1153, 0.1455, 0.8652, 0.3425])def calc_preds(coeffs, indeps): return torch.sigmoid((indeps*coeffs).sum(axis=1))coeffs = train_model(lr=100)0.510; 0.327; 0.294; 0.207; 0.201; 0.199; 0.198; 0.197; 0.196; 0.196; 0.196; 0.195; 0.195; 0.195; 0.195; 0.195; 0.195; 0.195; 0.194; 0.194; 0.194; 0.194; 0.194; 0.194; 0.194; 0.194; 0.194; 0.194; 0.194; 0.194; acc(coeffs)tensor(0.8258)show_coeffs(){'Age': tensor(-1.5061),
'SibSp': tensor(-1.1575),
'Parch': tensor(-0.4267),
'LogFare': tensor(0.2543),
'Sex_male': tensor(-10.3320),
'Sex_female': tensor(8.4185),
'Pclass_1': tensor(3.8389),
'Pclass_2': tensor(2.1398),
'Pclass_3': tensor(-6.2331),
'Embarked_C': tensor(1.4771),
'Embarked_Q': tensor(2.1168),
'Embarked_S': tensor(-4.7958)}tst_df = pd.read_csv(path/'test.csv')
tst_df| PassengerId | Pclass | Name | Sex | Age | SibSp | Parch | Ticket | Fare | Cabin | Embarked | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 892 | 3 | Kelly, Mr. James | male | 34.5 | 0 | 0 | 330911 | 7.8292 | NaN | Q |
| 1 | 893 | 3 | Wilkes, Mrs. James (Ellen Needs) | female | 47.0 | 1 | 0 | 363272 | 7.0000 | NaN | S |
| 2 | 894 | 2 | Myles, Mr. Thomas Francis | male | 62.0 | 0 | 0 | 240276 | 9.6875 | NaN | Q |
| 3 | 895 | 3 | Wirz, Mr. Albert | male | 27.0 | 0 | 0 | 315154 | 8.6625 | NaN | S |
| 4 | 896 | 3 | Hirvonen, Mrs. Alexander (Helga E Lindqvist) | female | 22.0 | 1 | 1 | 3101298 | 12.2875 | NaN | S |
| ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... |
| 413 | 1305 | 3 | Spector, Mr. Woolf | male | NaN | 0 | 0 | A.5. 3236 | 8.0500 | NaN | S |
| 414 | 1306 | 1 | Oliva y Ocana, Dona. Fermina | female | 39.0 | 0 | 0 | PC 17758 | 108.9000 | C105 | C |
| 415 | 1307 | 3 | Saether, Mr. Simon Sivertsen | male | 38.5 | 0 | 0 | SOTON/O.Q. 3101262 | 7.2500 | NaN | S |
| 416 | 1308 | 3 | Ware, Mr. Frederick | male | NaN | 0 | 0 | 359309 | 8.0500 | NaN | S |
| 417 | 1309 | 3 | Peter, Master. Michael J | male | NaN | 1 | 1 | 2668 | 22.3583 | NaN | C |
418 rows × 11 columns
tst_df['Fare'] = tst_df.Fare.fillna(0)tst_df.fillna(modes, inplace=True)
tst_df['LogFare'] = np.log(tst_df['Fare']+1)
tst_df = pd.get_dummies(tst_df, columns=["Sex","Pclass","Embarked"], dtype=float)
tst_indep = tensor(tst_df[indep_cols].values, dtype=torch.float)
tst_indep = tst_indep / vals# used trained coefficients to predict survival on test set
tst_df['Survived'] = (calc_preds(tst_indep, coeffs)>0.5).int()sub_df = tst_df[['PassengerId','Survived']]
sub_df| PassengerId | Survived | |
|---|---|---|
| 0 | 892 | 0 |
| 1 | 893 | 0 |
| 2 | 894 | 0 |
| 3 | 895 | 0 |
| 4 | 896 | 0 |
| ... | ... | ... |
| 413 | 1305 | 0 |
| 414 | 1306 | 1 |
| 415 | 1307 | 0 |
| 416 | 1308 | 0 |
| 417 | 1309 | 0 |
418 rows × 2 columns
Multiplying elements together and then adding across rows is identical to doing a matrix-vector product!
((val_indep*coeffs).sum(axis=1)).shapetorch.Size([178])(val_indep@coeffs).shapetorch.Size([178])def calc_preds(coeffs, indeps): return torch.sigmoid(indeps@coeffs)# need coeffs to be matrix for matrix products later on
def init_coeffs(): return (torch.rand(n_coeff, 1)*0.1).requires_grad_()# add new dimension
trn_dep = trn_dep[:,None]
val_dep = val_dep[:,None]trn_dep.shapetorch.Size([713, 1])coeffs = train_model(lr=100)0.512; 0.323; 0.290; 0.205; 0.200; 0.198; 0.197; 0.197; 0.196; 0.196; 0.196; 0.195; 0.195; 0.195; 0.195; 0.195; 0.195; 0.194; 0.194; 0.194; 0.194; 0.194; 0.194; 0.194; 0.194; 0.194; 0.194; 0.194; 0.194; 0.194; acc(coeffs)tensor(0.8258)First, we’ll need to create coefficients for each of our layers. Our first set of coefficients will take our
n_coeffinputs, and createn_hiddenoutputs. We can choose whatevern_hiddenwe like – a higher number gives our network more flexibility, but makes it slower and harder to train. So we need a matrix of sizen_coeffbyn_hidden. We’ll divide these coefficients byn_hiddenso that when we sum them up in the next layer we’ll end up with similar magnitude numbers to what we started with.
torch.rand(1)[0]tensor(0.6722)def init_coeffs(n_hidden=20):
layer1 = (torch.rand(n_coeff, n_hidden)-0.5)/n_hidden
layer2 = torch.rand(n_hidden, 1)-0.3
const = torch.rand(1)[0]
return layer1.requires_grad_(),layer2.requires_grad_(),const.requires_grad_()Now we have our coefficients, we can create our neural net. The key steps are the two matrix products,
indeps@l1andres@l2(whereresis the output of the first layer). The first layer output is passed toF.relu(that’s our non-linearity), and the second is passed totorch.sigmoidas before.
import torch.nn.functional as F
def calc_preds(coeffs, indeps):
l1,l2,const = coeffs # get the two linear layers and bias term
res = F.relu(indeps@l1) # matrix product of independent variable values and first linear layer, passed through non-linearity
res = res@l2 + const # matrix product of that result and second layer, plus constant
return torch.sigmoid(res) # that result passed through sigmoidFinally, now that we have more than one set of coefficients, we need to add a loop to update each one:
def update_coeffs(coeffs, lr):
for layer in coeffs:
layer.sub_(layer.grad * lr)
layer.grad.zero_()coeffs = train_model(lr=1.4)0.543; 0.532; 0.520; 0.505; 0.487; 0.466; 0.439; 0.407; 0.373; 0.343; 0.319; 0.301; 0.286; 0.274; 0.264; 0.256; 0.250; 0.245; 0.240; 0.237; 0.234; 0.231; 0.229; 0.227; 0.226; 0.224; 0.223; 0.222; 0.221; 0.220; coeffs = train_model(lr=20)0.543; 0.400; 0.260; 0.390; 0.221; 0.211; 0.197; 0.195; 0.193; 0.193; 0.193; 0.193; 0.193; 0.193; 0.193; 0.193; 0.193; 0.192; 0.192; 0.192; 0.192; 0.192; 0.192; 0.192; 0.192; 0.192; 0.192; 0.192; 0.192; 0.192; acc(coeffs)tensor(0.8258)torch.rand(1)tensor([0.1287])# deep learning
def init_coeffs():
hiddens = [10, 10] # <-- set this to the size of each hidden layer you want
sizes = [n_coeff] + hiddens + [1] # inputs, hidden layers, output
n = len(sizes)
layers = [(torch.rand(sizes[i], sizes[i+1])-0.3)/sizes[i+1]*4 for i in range(n-1)]
consts = [(torch.rand(1)[0]-0.5)*0.1 for i in range(n-1)]
for l in layers+consts: l.requires_grad_()
return layers,constsdef calc_preds(coeffs, indeps):
layers,consts = coeffs
n = len(layers)
res = indeps
for i,l in enumerate(layers):
res = res@l + consts[i]
if i!=n-1: res = F.relu(res)
return torch.sigmoid(res)def update_coeffs(coeffs, lr):
layers,consts = coeffs
for layer in layers+consts:
layer.sub_(layer.grad * lr)
layer.grad.zero_()coeffs = train_model(lr=4)0.521; 0.483; 0.427; 0.379; 0.379; 0.379; 0.379; 0.378; 0.378; 0.378; 0.378; 0.378; 0.378; 0.378; 0.378; 0.378; 0.377; 0.376; 0.371; 0.333; 0.239; 0.224; 0.208; 0.204; 0.203; 0.203; 0.207; 0.197; 0.196; 0.195; acc(coeffs)tensor(0.8258)Continuing with video notes:
We initialized coeffs (coeficients) and a bias term const and updated them by going through each layers and subtracting out the gradient .grad multiplied by the learning rate lr.
In PyTorch, we don’t have to keep track of what our coefficients (or parameters, or weights) are, PyTorch does that for us. It does that by looking inside our Module and trying to find anything that looks like a tensor of neural net Parameters and it keeps track of them.
Creating out own model in PyTorch:
from fastai.collab import *
from fastai.tabular.all import *class T(Module):
def __init__(self): self.a = torch.ones(3)
L(T().parameters())(#0) []PyTorch looks inside our Module and keeps track of anything that looks like a tensor of neural network parameters. We can find out what parameters in general PyTorch knows about in our model by instantiating our model and then asking for the parameters.
The way you tell PyTorch what your parameter are is by putting them inside a special object called nn.Parameter which hardly does anything—they key thing it does is that when PyTorch checks to see which parameters should it update when it optimizes, it just looks for anything that’s been wrapped in this class.
class T(Module):
def __init__(self): self.a = nn.Parameter(torch.ones(3))
L(T().parameters()) # by default assumes that we're going to want to require gradient(#1) [Parameter containing:
tensor([1., 1., 1.], requires_grad=True)]class T(Module):
def __init__(self): self.a = nn.Linear(1, 3, bias=False) # automatically considered a parameter by PyTorch
L(T().parameters())(#1) [Parameter containing:
tensor([[-0.5822],
[ 0.4630],
[-0.4310]], requires_grad=True)]t = T()
type(t.a.weight)torch.nn.parameter.ParameterWe want to create something that works like an Embedding which creates a matrix which will be trained as we train the model, something we can index into (during the forward pass).
user_bias will be a vector of parameters, user_factors will be matrix.
When you put a tensor inside nn.Parameter it has all the features a tensor has (for example, we can index into it).
The create_params function is all that’s required to recreate PyTorch’s Embedding layer from scratch.
def create_params(size):
return nn.Parameter(torch.zeros(*size).normal_(0, 0.01))class DotProductBias(Module):
def __init__(self, n_users, n_movies, n_factors, y_range=(0, 5.5)):
self.user_factors = create_params([n_users, n_factors])
self.user_bias = create_params([n_users])
self.movie_factors = create_params([n_movies, n_factors])
self.movie_bias = create_params([n_movies])
self.y_range = y_range
def forward(self, x):
users = self.user_factors[x[:, 0]]
movies = self.movie_factors[x[:, 1]]
res = (users*movies).sum(dim=1)
res += self.user_bias[x[:,0]]+self.movie_bias[x[:,1]]
return sigmoid_range(res, *self.y_range)Let’s see if it trains:
path = untar_data(URLs.ML_100k)
ratings = pd.read_csv(path/'u.data', delimiter='\t', header=None, names=['user', 'movie', 'rating', 'timestamp'])
movies = pd.read_csv(path/'u.item', delimiter='|', encoding='latin-1', usecols=(0,1), names=('movie', 'title'), header=None)
ratings = ratings.merge(movies)
dls = CollabDataLoaders.from_df(ratings, item_name='title', bs=64)
n_users = len(dls.classes['user'])
n_movies = len(dls.classes['title'])model = DotProductBias(n_users, n_movies, 50)
learn = Learner(dls, model, loss_func=MSELossFlat())
learn.fit_one_cycle(5, 5e-3, wd=0.1)| epoch | train_loss | valid_loss | time |
|---|---|---|---|
| 0 | 0.882364 | 0.953949 | 00:11 |
| 1 | 0.654987 | 0.886329 | 00:10 |
| 2 | 0.521378 | 0.869882 | 00:10 |
| 3 | 0.444553 | 0.858153 | 00:09 |
| 4 | 0.429629 | 0.853653 | 00:10 |
model.movie_bias # a parameter containing a bunch of numbers that have been trainedParameter containing:
tensor([-0.0033, -0.1991, 0.0095, ..., 0.0080, 0.1408, 0.0015],
requires_grad=True)model.movie_bias.shape # 1665 moviestorch.Size([1665])In PyTorch, a method that ends in an underscore changes in place the tensor it’s being applied to.
torch.zeros([4])tensor([0., 0., 0., 0.])torch.zeros([4]).normal_(0, 0.01)tensor([-0.0008, -0.0040, 0.0108, -0.0071])We trained this model—but what did it do? How is it going about predicting who’s going to like what movie?
We can find which movies have the highest and lowest movie bias. We can grab the names of those movies from our DataLoaders for each of those 5 lowest or highest numbers.
learn.model.movie_bias.shape, learn.model.movie_bias.squeeze().shape(torch.Size([1665]), torch.Size([1665]))The movies with the lowest movie_bias values are some pretty crappy movies. Why is that? That’s because when it does that matrix product it’s trying to figure out who’s going to like what movie based on previous movies people have enjoyed or not, and then it adds movie bias, which can be positive or negative, that’s a different number for each movie. In order to do a good job at predicting whether you’re going to like a movie or not, it has to know which movies are crap. So that crap movies are going to end up with a very low movie bias parameter. We can find out not only which movies do people really not like, but which movies do people like less than one would expect given the kind of movie that it is?
So “Lawnmower Man 2”, not only is it a crappy movie but based on the kind of movie it is (kind of like a high-tech pop kind of sci-fi movie) people who like those kinds of movies still don’t like “Lawnmower Man 2”. In this way we can use a model not just to predict things but to understand things about the data.
movie_bias = learn.model.movie_bias.squeeze()
idxs = movie_bias.argsort()[:5]
[dls.classes['title'][i] for i in idxs], movie_bias.sort()[0][:5](['Lawnmower Man 2: Beyond Cyberspace (1996)',
'Children of the Corn: The Gathering (1996)',
'Grease 2 (1982)',
'Beverly Hills Ninja (1997)',
'Island of Dr. Moreau, The (1996)'],
tensor([-0.3312, -0.3286, -0.2666, -0.2655, -0.2578], grad_fn=<SliceBackward0>))If we sort be descending, it’ll give us the exact opposite. Here are movies that people enjoy, even when they don’t enjoy that kind of movie.
idxs = movie_bias.argsort(descending=True)[:5]
[dls.classes['title'][i] for i in idxs], movie_bias.sort(descending=True)[0][:5](['Shawshank Redemption, The (1994)',
'Star Wars (1977)',
'L.A. Confidential (1997)',
"Schindler's List (1993)",
'Titanic (1997)'],
tensor([0.5890, 0.5813, 0.5789, 0.5435, 0.5397], grad_fn=<SliceBackward0>))We can do the same with users and find out which users just loves movies, even the crappy ones and vice versa.
# users who don't like any movies
user_bias = learn.model.user_bias.squeeze()
idxs = user_bias.argsort()[:5]
[dls.classes['user'][i] for i in idxs], user_bias.sort()[0][:5]([181, 405, 724, 774, 445],
tensor([-0.7536, -0.5753, -0.4381, -0.4175, -0.3963], grad_fn=<SliceBackward0>))# users who like all movies
user_bias = learn.model.user_bias.squeeze()
idxs = user_bias.argsort(descending=True)[:5]
[dls.classes['user'][i] for i in idxs], user_bias.sort(descending=True)[0][:5]([907, 295, 507, 472, 849],
tensor([0.7339, 0.6750, 0.6721, 0.6689, 0.6160], grad_fn=<SliceBackward0>))What about the latent factors? We can do something called Principal Component Analysis which compresses those 50 columns of latent factors down to (however many you specify).
g = ratings.groupby('title')['rating'].count()
gtitle
'Til There Was You (1997) 9
1-900 (1994) 5
101 Dalmatians (1996) 109
12 Angry Men (1957) 125
187 (1997) 41
...
Young Guns II (1990) 44
Young Poisoner's Handbook, The (1995) 41
Zeus and Roxanne (1997) 6
unknown 9
Á köldum klaka (Cold Fever) (1994) 1
Name: rating, Length: 1664, dtype: int64top_movies = g.sort_values(ascending=False).index.values[:1000]
top_movies[:5]array(['Star Wars (1977)', 'Contact (1997)', 'Fargo (1996)',
'Return of the Jedi (1983)', 'Liar Liar (1997)'], dtype=object)top_idxs = tensor([learn.dls.classes['title'].o2i[m] for m in top_movies])
top_idxs[:5]tensor([1399, 334, 499, 1235, 861])movie_w = learn.model.movie_factors[top_idxs].cpu().detach()
movie_w.shapetorch.Size([1000, 50])movie_pca = movie_w.pca(3)
movie_pca.shapetorch.Size([1000, 3])fac0, fac1, fac2 = movie_pca.t()
fac0.shape, fac1.shape, fac2.shape(torch.Size([1000]), torch.Size([1000]), torch.Size([1000]))idxs = list(range(50))
X = fac0[idxs]
Y = fac2[idxs]
plt.figure(figsize=(12,12))
plt.scatter(X, Y)
for i, x, y in zip(top_movies[idxs], X, Y):
plt.text(x,y,i, color=np.random.rand(3)*0.7, fontsize=11)
plt.show() # compressed view of the latent factorsfastai provides a collab_learner:
learn = collab_learner(dls, n_factors=50, y_range=(0, 5.5))learn.fit_one_cycle(5, 5e-3, wd=0.1)| epoch | train_loss | valid_loss | time |
|---|---|---|---|
| 0 | 0.907180 | 0.950933 | 00:17 |
| 1 | 0.657494 | 0.902355 | 00:11 |
| 2 | 0.501019 | 0.877131 | 00:11 |
| 3 | 0.444013 | 0.865720 | 00:12 |
| 4 | 0.409778 | 0.861589 | 00:11 |
learn.modelEmbeddingDotBias(
(u_weight): Embedding(944, 50)
(i_weight): Embedding(1665, 50)
(u_bias): Embedding(944, 1)
(i_bias): Embedding(1665, 1)
)movie_bias = learn.model.i_bias.weight.squeeze()
idxs = movie_bias.argsort(descending=True)[:5]
[dls.classes['title'][i] for i in idxs], movie_bias.sort(descending=True)[0][:5](['Shawshank Redemption, The (1994)',
'L.A. Confidential (1997)',
'Good Will Hunting (1997)',
"Schindler's List (1993)",
'Star Wars (1977)'],
tensor([0.6044, 0.5852, 0.5647, 0.5546, 0.5231], grad_fn=<SliceBackward0>))The fastai model for collaborative filtering (without Neural Network) is pretty much identical to the DotProductBias model we created from scratch. Here’s its forward method:
def forward(self, x):
users,items = x[:,0],x[:,1]
dot = self.u_weight(users)* self.i_weight(items)
res = dot.sum(1) + self.u_bias(users).squeeze() + self.i_bias(items).squeeze()
if self.y_range is None: return res
return torch.sigmoid(res) * (self.y_range[1]-self.y_range[0]) + self.y_range[0]movie_factors = learn.model.i_weight.weight
idx = dls.classes['title'].o2i['Silence of the Lambs, The (1991)']distances = nn.CosineSimilarity(dim=1)(movie_factors, movie_factors[idx][None]) # calculate how far apart each embedding is from the Silence of the Lambs
# CosineSimilarity is basically the angle between the vectors
distances.shapetorch.Size([1665])idx = distances.argsort(descending=True)[1] # the closest movie to Silence of the Lambs
dls.classes['title'][idx]'Casablanca (1942)'We can use Deep Learning instead of dot products.
class CollabNN(Module):
def __init__(self, user_sz, item_sz, y_range=(0,5.5), n_act=100):
self.user_factors = Embedding(*user_sz)
self.item_factors = Embedding(*item_sz)
self.layers = nn.Sequential( # layers of a neural network in order
nn.Linear(user_sz[1]+item_sz[1], n_act),
nn.ReLU(),
nn.Linear(n_act, 1)
)
self.y_range = y_range
def forward(self, x):
embs = self.user_factors(x[:,0]), self.item_factors(x[:,1])
x = self.layers(torch.cat(embs, dim=1)) # concatenate the user and item embeddings with torch.cat
return sigmoid_range(x, *self.y_range)Ask fastai how big our NN embeddings should be (based on a formula that matches Jeremy’s intuition):
embs = get_emb_sz(dls)
embs[(944, 74), (1665, 102)]get_emb_sz??model = CollabNN(*embs)learn = Learner(dls, model, loss_func=MSELossFlat())
learn.fit_one_cycle(5, 5e-3, wd=0.1)| epoch | train_loss | valid_loss | time |
|---|---|---|---|
| 0 | 0.918632 | 0.965365 | 00:15 |
| 1 | 0.868667 | 0.928044 | 00:14 |
| 2 | 0.825990 | 0.911105 | 00:16 |
| 3 | 0.777693 | 0.879813 | 00:26 |
| 4 | 0.767727 | 0.872732 | 00:19 |
learn = collab_learner(dls, use_nn=True, y_range=(0, 5.5), layers=[100, 50])
learn.fit_one_cycle(5, 5e-3, wd=0.1)| epoch | train_loss | valid_loss | time |
|---|---|---|---|
| 0 | 0.953472 | 1.010605 | 00:17 |
| 1 | 0.891541 | 0.936580 | 00:16 |
| 2 | 0.816217 | 0.904296 | 00:17 |
| 3 | 0.758014 | 0.884302 | 00:15 |
| 4 | 0.749216 | 0.878866 | 00:15 |
The dot product version is doing better because it’s taking advantage of our understanding of the problem domain. In practice, companies create a combined model with a dot product component and also has a neural net component. The neural net component is particularly helpful if you have metadata. You can concatenate that in with your embeddings.
In collaborative filtering in general there’s an issue where a small number of users and movies overwhelm everybody else. A classic one is anime (small number of viewers who watch it a lot). You have to be careful about these subtlety issues, involves taking various ratios or normalizing things.
Embeddings are not just for collaborative filtering. You’ve probably heard about them in the context of Natural Language Processing (NLP). How do we go about using text as inputs to models? You can turn words into integers—taking the unique words from a text and assigning them an id. We then create an embedding matrix for those words. To give this text to a neural net, we list out our words, and for each word we look up the word id (MATCH in Excel) and then find that word’s embeddings using OFFSET. You can then train the embeddings and then interpret them as we’ve done with movie bias factors and the latent factors.
Our different models, the inputs to them are based on a relatively small number of basic principles. These principles are generally thinks like “look up something in an array.” And then we know inside the model we’re multiplying things, adding them up and replacing the negatives with 0s.
In tabular_learner it creates an Embedding for each of the categorical variables (from number of inputs to number of factors based on get_emb_sz). In its forward pass, if there’s embeddings it’ll go through and pass the inputs into them and concatenate the results, and run it through the neural net layers.
You can create your neural net, get your trained embeddings and put those embeddings into a random forest or gradient boosted tree and you’re mean average percent error will dramatically improve.
Convolutions
We’ve learned about what goes into the model (categories, embeddings, or continuous numbers). We’ve learned about what comes out the other side (a bunch of activations—a tensor of numbers) which we can use things like softmax to constrain them to add up to 1. We’ve looked at what can go in the middle which is the matrix multiplication sandwiched together with rectified linear units. There are other things that can go in the middle, which is convolutions (another kind of matrix multiplication).
Convolutional Neural Networks are similar to what we’ve seen so far (inputs, things that are a form of matrix multiplication, sandwiched with activation functions). But there’s a particular thing that makes them very useful for computer vision.
Back in the mid-90s, Yann LeCun showed really practically useful performance on this dataset which resulted in convnets being used in the american banking system for reading checks.
In the Excel file, Jeremy has recreated a 28x28 cell “7” from the MNIST dataset and is multiplying each 3x3 cells with the following filter:
| 1 | 1 | 1 |
| 0 | 0 | 0 |
| -1 | -1 | -1 |
and taking the max of that dot product and 0. It’s like ReLU but it’s not doing a matrix product, it’s doing a dot product just on those 9 cells (3x3) and just those 9 weights (the 3x3 “filter”). When you move one to the right, it’s using the next 9 cells, and so on.
A convolution is when you slide a little 3x3 matrix across a bigger matrix and at each location you do a dot product of that 3x3 matrix with the 3x3 matrix of coefficients. Why does that create something that finds something like top edges? It’s because of the way we’ve constructed the coefficient matrix.
All of the rows just above are going to get a 1. All of the ones just below are going to get a -1. And all of the ones in the middle are going to get a 0. When the image’s 3x3 is:
| 1 | 1 | 1 |
| 1 | 1 | 1 |
| 1 | 1 | 1 |
Multiplying it by the filter:
| 1 | 1 | 1 |
| 0 | 0 | 0 |
| -1 | -1 | -1 |
Gives us 0. But when the image’s 3x3 is something like:
| 1 | 1 | 1 |
| 0.8 | 0.8 | 0.8 |
| 0 | 0 | 0 |
Multiplying it by the filter gives us 3. We’ll only get such 3s when the image’s 3x3 has the top row as dark as possible (1) and the bottom row blank (0). That’s only going to happen at a horizontal edge.
A horizontal edge detector is the filter of coefficients:
| 1 | 0 | -1 |
| 1 | 0 | -1 |
| 1 | 0 | -1 |
The dot product will only be 3 where the 3x3’s leftmost column is 1’s and the rightmost is 0’s.
You can think of a convolution as being a sliding window, of little mini dot products of these little 3x3 matrices. They don’t have to be 3x3 we could have just as easily done 5x5 then we’d have a 5x5 matrix of coefficients. Whatever size you like. The size is called the kernel size. A 3x3 kernel for this convolution.
We repeat these steps again and again. In the second layer we now have two channels. In the first layer we just had one (the grayscale original image). The two channels are the horizontal edges channel and the vertical edges channel. Our filter is now 3x3x2 or two 3x3 kernels or one 3x3x2 kernel. It combines the horizontal and the vertical edge detectors.
We’ll eventually end up with a single set of 10 activations (one for each digit 0-9) or 1 activation (7 or not-7). We’d back propogate through these calculations using SGD. And that is going to end up optimizing the coefficients in the filters. In real life you start with random numbers and then optimize them with SGD (instead of the manual edge detectors Jeremy instantiated).
A few years what we used was max pooling—which is like a convolution except you don’t take a dot product you take the max of a sliding window (in our case, a 2x2 max pooling). With a 2x2 max pooling, we end up losing half of our activations on each dimension, so we’re going to end up with only 1/4th the activations that we started out with. And that’s a good thing because if we keep doing conv layers and max pools, will have fewer and fewer activations, then we take a dot product of those with a bunch of coefficients (dense layer) for each channel and then add them all up for our final big dot product. MNIST would have 10 such final activations, with a softmax layer after that.
Nowadays we normally don’t have max pool layers. But instead when we do our sliding window, we skip one every time we move to the next 3x3 (after doing column I we skip column J and go straight to K). That’s called a “stride 2” convolution. So every time we do a convolution we reduce our effective feature size by 2 on each axis (reducing by 4x in total), instead of doing max pooling.
The other thing is nowadays we don’t have a single dense layer but instead we keep doing stride-2 convolutions until we’ve got about a 7x7 grid, and then we do a single pooling at the end (average instead of max). So we average the activations of each one of the 7x7 features. This is important know to because something like an imagenet style image detector is going to end up with a 7x7 grid for “is this a bear?” and for each of the 7x7 squares it’s seeing if there is a bear in that part of the photo, and it takes the average of those 49 predictions to decide whether there’s a bear in the photo. That works very well if it’s basically a photo of a bear. If the bear is big and takes up most of the frame, then most of the 7x7 bits are bits of the bear. On the other hand, if there’s a teeny tiny bear in the corner, then potentially only one of those 49 squares has a bear in it. Even worse, if it’s a picture with lots of different things only one of which is a bear—it could end up being not a good bear detector. The details of how we construct our model turn out to be important. If you’re trying to find one part of the photo that has a bear in it, you might want to try max pooling (“i think this is a picture of a bear if any one of the 49 bits has a bear in it”). The max/average pool is happening right at the very end. fastai does max pool and average pool and concatenate them together (concat pooling) and that has since been reinvented in at least one paper.
Convolution is the same thing as a matrix multiplication. Here is convolution as a sliding window—
the kernel
| \(\alpha\) | \(\beta\) |
| \(\gamma\) | \(\delta\) |
and a 3x3 image:
| A | B | C |
| D | E | F |
| G | H | J |
and the resulting convolution
| P | Q |
| R | S |
I’ll show the first sliding window multiplication (in italics/bold):
| A | B | C |
| D | E | F |
| G | H | J |
Which is:
\(\alpha A+\beta B+ \gamma D + \delta E + b = P\)
and the rest of the sliding windows:
| A | B | C |
| D | E | F |
| G | H | J |
\(\alpha B+\beta C+ \gamma E + \delta F + b = Q\)
| A | B | C |
| D | E | F |
| G | H | J |
\(\alpha D+\beta E+ \gamma G + \delta H + b = R\)
| A | B | C |
| D | E | F |
| G | H | J |
\(\alpha E+\beta F+ \gamma H + \delta J + b = S\)
We can also write it as a matrix multiplication. This matrix of kernel or filter values:
| \(\alpha\) | \(\beta\) | 0 | \(\gamma\) | \(\delta\) | 0 | 0 | 0 | 0 |
| 0 | \(\alpha\) | \(\beta\) | 0 | \(\gamma\) | \(\delta\) | 0 | 0 | 0 |
| 0 | 0 | \(\alpha\) | \(\beta\) | 0 | \(\gamma\) | \(\delta\) | 0 | 0 |
| 0 | 0 | 0 | \(\alpha\) | \(\beta\) | 0 | \(\gamma\) | \(\delta\) | 0 |
| 0 | 0 | 0 | 0 | \(\alpha\) | \(\beta\) | 0 | \(\gamma\) | \(\delta\) |
Multiplied by a column of pixels:
| A | |
| B | |
| C | |
| D | |
| E | |
| F | |
| G | |
| H | |
| J |
plus a column of biases:
| b | |
| b | |
| b | |
| b |
yields the convolution:
| P | |
| Q | |
| R | |
| S |
In practice it’s faster to do it as a sliding window but this matrix multiplication is a good way to think about it as a special type of matrix multiplication.
Dropout
Same convolutions as before, followed by a bunch of random numbers. We define a dropout factors (from 0.0 to 0.9) which we use to create a dropout mask (if the random number in a given cell/pixel is greater than the dropout factor, use that random number otherwise set it to 0). We start with the image and then corrupt it (random bits of it have been deleted). Higher dropout factor will delete more of the picture. That “corrupted” image is the input to the next layer (which is max pool in our example).
Why would we delete some data at random from our processed image/activations after convolutions? The reason is that a human is able to look at the corrupted image and still recognize it’s a 7. A computer should be able to as well. If we randomly delete different bits of the activations each time, then the computer is forced to learn the underlying real representation rather than overfitting. Think of this as data augmentations for the activations. This is called a Dropout layer, which is really helpful for avoiding overfitting. The more dropout you use, the less good it will be on the training data but the better it ought to generalize.
A different set of activations will be deleted each batch. Dropout was initially rejected by NIPS, disseminated by arxiv. Peer-review is a very fallible thing in both directions.
Part 1 Summary
We’ve seen quite a few ways of dealing with inputs to neural networks, things that can happen in the middle of the NN. We’ve talked about Rectified Linear Units (ReLU) (0 if x is less than 0 or x otherwise), there are other activations you can use (except for Identity, with which you end up with a linear model)—these don’t matter very much, any non-linearity works fine–inputs can be one-hot encoded (or embeddings which is a computational shortcut), there are sandwiched layers of matrix multipliers and activation functions, matrix multipliers can be special cases like convolutions or embeddings, the output can go through some tweaking such as Softmax, and you’ve got the loss function such as cross-entropy loss or mean squared error or mean absolute error.
AMA
Read Radek’s book “Meta Learning”. One of the fastai alums went on to create the Mish activation function now used in many SOTA models around the world and is now at Mila, one of the top research labs of the world.
How do you stay motivated? You don’t have to know everything—nobody know’s everything and that’s okay. Take an interest in some area and follow that and do the best job of keeping up with some little sub area. If you’re sub area is too much to keep up on, pick a sub-sub area. From time to time, take a dip into other areas you’re not following as closely. Things are not changing that fast at all. Fundamentally the stuff that is in the course now is not that different to what was in the course five years ago. The foundations haven’t changed. It’s not that different to the convolutional neural network that Yann LeCun used on MNIST back in 1996. The basic ideas are forever. Everything else is tweaks. The more you learn about the basic ideas, the more you’ll recognize those tweaks as simple little tricks that you’ll quickly be able to get your head around.
The key thing to creating a legitimate business venture is to solve a legitimate problem. A problem that people need solving and will pay you to solve. It’s important not to start with your fun gradio prototype as the basis for your business, but instead start with: here’s a problem that I want to solve. Pick a problem that you understand better than most people. Eric Reis wrote “The Lean Startup” who recommends that what you do next is you fake it. You create a Minimum Viable Product—something that solves the problem that takes as little time to create. It could be very manual, it could be loss making, that’s fine. The bit in the middle where there’s going to be a neural net—you launch without it and do everything by hand. You’re just trying to find out: “are people going to pay for this? is this actually useful?” Once you have confirmed that the need is real and that people will pay for it and you can solve the need you can gradually make it less fake and more and more getting the product to where you want it to be.
Productivity hacks: not to work too much. Jeremy spends less hours a day working than most people. Jeremy has spent half of every working day since 18 learning or practicing something new. Doing it more slowly than if he used something that he already knew. In the other 50% of the time he’s constantly building up, exponentially, this base of expertise in a wide range of areas so he can do things multiples or orders of magnitudes faster than people around him. Try not overdo things, get good sleep, eat well and exercise well. It’s also a case of tenacity—Jeremy has noticed a lot of people give up much earlier than he does. If you just keep going until something’s actually finished (nicely), then that’s going to put you in a small minority. Most people don’t do that. Jeremy makes things like nbdev that make it easier to finish something nicely. Make the things that you want to do easier so that you’ll do them more.
Book Notes
feature engineering: creating new transformations of the input data in order to make it easier to model.
In the context of an image, a feature is a visually distinctive attribute.
Finding the edges in an image is a very common task in computer vision and to do it we use something called a convolution which requires nothing more than multiplication and addition. Let’s do this with code:
from fastai.vision.all import *
matplotlib.rc('image', cmap='Greys')top_edge = tensor([[-1, -1, -1],
[ 0, 0, 0],
[ 1, 1, 1]])
top_edge # this is our kerneltensor([[-1, -1, -1],
[ 0, 0, 0],
[ 1, 1, 1]])path = untar_data(URLs.MNIST_SAMPLE)Multiply the top 3x3-pixel square of our image and multiply each of those values by each item in our kernel, then add them up.
im3_t = tensor(im3)
im3_t[0:3, 0:3] * top_edgetensor([[0, 0, 0],
[0, 0, 0],
[0, 0, 0]])(im3_t[0:3, 0:3] * top_edge).sum()tensor(0)# more interesting results
df = pd.DataFrame(im3_t[:10, :20])
df.style.set_properties(**{'font-size': '6pt'}).background_gradient('Greys')| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 2 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 3 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 4 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 5 | 0 | 0 | 0 | 12 | 99 | 91 | 142 | 155 | 246 | 182 | 155 | 155 | 155 | 155 | 131 | 52 | 0 | 0 | 0 | 0 |
| 6 | 0 | 0 | 0 | 138 | 254 | 254 | 254 | 254 | 254 | 254 | 254 | 254 | 254 | 254 | 254 | 252 | 210 | 122 | 33 | 0 |
| 7 | 0 | 0 | 0 | 220 | 254 | 254 | 254 | 235 | 189 | 189 | 189 | 189 | 150 | 189 | 205 | 254 | 254 | 254 | 75 | 0 |
| 8 | 0 | 0 | 0 | 35 | 74 | 35 | 35 | 25 | 0 | 0 | 0 | 0 | 0 | 0 | 13 | 224 | 254 | 254 | 153 | 0 |
| 9 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 90 | 254 | 254 | 247 | 53 | 0 |
im3_t[4:7, 6:9] # top edgetensor([[ 0, 0, 0],
[142, 155, 246],
[254, 254, 254]], dtype=torch.uint8)im3_t[4:7, 6:9] * top_edgetensor([[ 0, 0, 0],
[ 0, 0, 0],
[254, 254, 254]])(im3_t[4:7, 6:9] * top_edge).sum()tensor(762)im3_t[7:10, 17:20] # right edgetensor([[254, 75, 0],
[254, 153, 0],
[247, 53, 0]], dtype=torch.uint8)im3_t[7:10, 17:20] * top_edgetensor([[-254, -75, 0],
[ 0, 0, 0],
[ 247, 53, 0]])(im3_t[7:10, 17:20] * top_edge).sum()tensor(-29)This calculation is returning a high number where the 3x3-pixel square represents a top edge (where there are low values at the top of the square and high values immediately underneath)—in that case the -1 values in our kernel have little impact.
Looking at the math, any window of size 3x3 in our image:
| a1 | a2 | a3 |
| a4 | a5 | a6 |
| a7 | a8 | a9 |
Multiplying by a kernel:
| 1 | 1 | 1 |
| 0 | 0 | 0 |
| -1 | -1 | -1 |
Will return:
a1 + a2 + a3 - a7 - a8 - a9.
If a1 = a7, a2 = a8, and a3 = a9, we’ll get 0. If a1 > a7, a2 > a8 and a3 > a9 we’ll get a positive number. This filter detects horizontal edges.
The kernel:
| -1 | -1 | -1 |
| 0 | 0 | 0 |
| 1 | 1 | 1 |
detects horizontal edges where we go from light to dark.
The kernel:
| 1 | 1 | 1 |
| 0 | 0 | 0 |
| -1 | -1 | -1 |
detects horizontal edges where we go from dark to light.
The kernel:
| 1 | 0 | -1 |
| 1 | 0 | -1 |
| 1 | 0 | -1 |
detects vertical edges where we go from dark (left) to light (right).
The kernel:
| -1 | 0 | 1 |
| -1 | 0 | 1 |
| -1 | 0 | 1 |
detects vertical edges where we go from light (left) to dark (right).
import matplotlib.pyplot as plt
import seaborn as sns
import pandas as pd
from torch import tensor
# Create the tensor
data = tensor([[254, 0, 0],
[254, 0, 0],
[254, 0, 0]])
# Convert the tensor to a Pandas DataFrame
df = pd.DataFrame(data.numpy())
# Plot the heatmap
plt.figure(figsize=(3, 3))
sns.heatmap(df, annot=True, cmap='Greys', cbar=False, linewidths=.5, fmt='d')
plt.show()# vertical edge detector (light to dark - left to right)
k = tensor([[-1, 0, 1],
[-1, 0, 1],
[-1, 0, 1]])
data = tensor([[254, 0, 0],
[254, 0, 0],
[254, 0, 0]])
res = data * k
# Convert the tensor to a Pandas DataFrame
df = pd.DataFrame(res.numpy())
# Plot the heatmap
plt.figure(figsize=(3, 3))
sns.heatmap(df, annot=True, cmap='Greys', cbar=False, linewidths=.5, fmt='d')
plt.show()# vertical edge detector (dark to light - left to right)
k = tensor([[1, 0, -1],
[1, 0, -1],
[1, 0, -1]])
data = tensor([[254, 0, 0],
[254, 0, 0],
[254, 0, 0]])
res = data * k
# Convert the tensor to a Pandas DataFrame
df = pd.DataFrame(res.numpy())
# Plot the heatmap
plt.figure(figsize=(3, 3))
sns.heatmap(df, annot=True, cmap='Greys', cbar=False, linewidths=.5, fmt='d')
plt.show()Let’s create a function to do this for one location, and check that it matches our result from before:
def apply_kernel(row, col, kernel):
return (im3_t[row-1:row+2, col-1:col+2] * kernel).sum()apply_kernel(5, 7, top_edge)tensor(762)l = [0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10]
l[5-1:5+2], l[7-1: 7+2]([4, 5, 6], [6, 7, 8])254*3762Note that we can’t apply this to a corner since there isn’t a complete 3x3 square there.
Mapping a Convolutional Kernel
We can map apply_kernel across the coordinate grid—taking our 3x3 kernel and applying it to each 3x3 section of our image.
To get a grid of coordinates, use a nested list comprehension:
[[(i, j) for j in range(1,5) for i in range(1,5)]][[(1, 1),
(2, 1),
(3, 1),
(4, 1),
(1, 2),
(2, 2),
(3, 2),
(4, 2),
(1, 3),
(2, 3),
(3, 3),
(4, 3),
(1, 4),
(2, 4),
(3, 4),
(4, 4)]][[(i, j) for i in range(1,5) for j in range(1,5)]][[(1, 1),
(1, 2),
(1, 3),
(1, 4),
(2, 1),
(2, 2),
(2, 3),
(2, 4),
(3, 1),
(3, 2),
(3, 3),
(3, 4),
(4, 1),
(4, 2),
(4, 3),
(4, 4)]][[(i, j) for i in ['inner1', 'inner2', 'inner3'] for j in ['outer1', 'outer2', 'outer3']]][[('inner1', 'outer1'),
('inner1', 'outer2'),
('inner1', 'outer3'),
('inner2', 'outer1'),
('inner2', 'outer2'),
('inner2', 'outer3'),
('inner3', 'outer1'),
('inner3', 'outer2'),
('inner3', 'outer3')]]# applying kernel over coordinate grid
rng = range(1,27)
top_edge3 = tensor([[apply_kernel(i, j, top_edge) for j in rng] for i in rng])
show_image(top_edge3);tensor([[apply_kernel(i, j, top_edge) for j in rng] for i in rng]).shape, \
tensor([[apply_kernel(i, j, top_edge) for j in rng for i in rng]]).shape, \
tensor([[apply_kernel(i, j, top_edge) for i in rng] for j in rng]).shape, \
tensor([[apply_kernel(i, j, top_edge)] for j in rng for i in rng]).shape(torch.Size([26, 26]),
torch.Size([1, 676]),
torch.Size([26, 26]),
torch.Size([676, 1]))# left edge
left_edge = tensor([[-1, 1, 0],
[-1, 1, 0],
[-1, 1, 0]]).float()
left_edge3 = tensor([[apply_kernel(i, j, left_edge) for j in rng] for i in rng])
show_image(left_edge3);# right edge
right_edge = tensor([[0, 1, -1],
[0, 1, -1],
[0, 1, -1]]).float()
right_edge3 = tensor([[apply_kernel(i, j, right_edge) for j in rng] for i in rng])
show_image(right_edge3);top_edgetensor([[-1, -1, -1],
[ 0, 0, 0],
[ 1, 1, 1]])# bottom edge
bottom_edge = tensor([[1, 1, 1],
[0, 0, 0],
[-1, -1, -1]]).float()
bottom_edge3 = tensor([[apply_kernel(i, j, bottom_edge) for j in rng] for i in rng])
show_image(bottom_edge3);# top right diagonal
top_right_diagonal = tensor([[1, -1, -1],
[0, 1, -1],
[0, 0, 1]]).float()
top_right_diagonal3 = tensor([[apply_kernel(i, j, top_right_diagonal) for j in rng] for i in rng])
show_image(top_right_diagonal3);# top left diagonal
top_left_diagonal = tensor([[-1, -1, 0],
[-1, 0, 1],
[ 0, 1, 1]]).float()
top_left_diagonal3 = tensor([[apply_kernel(i, j, top_left_diagonal) for j in rng] for i in rng])
show_image(top_left_diagonal3);# bottom right diagonal
bottom_right_diagonal = tensor([[1, 1, 0],
[1, 0, -1],
[0, -1, -1]]).float()
bottom_right_diagonal3 = tensor([[apply_kernel(i, j, bottom_right_diagonal) for j in rng] for i in rng])
show_image(bottom_right_diagonal3);# bottom left diagonal
bottom_left_diagonal = tensor([[ 0, 1, 1],
[-1, 0, 1],
[-1, -1, 0]]).float()
bottom_left_diagonal3 = tensor([[apply_kernel(i, j, bottom_left_diagonal) for j in rng] for i in rng])
show_image(bottom_left_diagonal3);A image with height h and width w will have h-2 by w-2 3x3 windows. In our case we have 28x28 image, and 26x26 resulting convolutions.
Convolutions in PyTorch
PyTorch wants a rank-4 tensor as input (minibatch, in_channels, iH, iW) and weight (out_channels, in_channels, kH, kW) so that it can apply a convolution to multiple images at the same time (every item in a batch at once) and apply multiple kernels at the same time.
diag1_edge = tensor([[ 0, -1, 1],
[-1, 1, 0],
[ 1, 0, 0]]).float()
diag1_edge3 = tensor([[apply_kernel(i, j, diag1_edge) for j in rng] for i in rng])
show_image(diag1_edge3);diag2_edge = tensor([[1, -1, 0],
[0, 1, -1],
[0, 0, 1]])
diag2_edge3 = tensor([[apply_kernel(i, j, diag2_edge) for j in rng] for i in rng])
show_image(diag2_edge3);edge_kernels = torch.stack([left_edge, top_edge, diag1_edge, diag2_edge])
edge_kernels.shapetorch.Size([4, 3, 3])mnist = DataBlock((ImageBlock(cls=PILImageBW), CategoryBlock),
get_items=get_image_files,
splitter=GrandparentSplitter(),
get_y=parent_label)dls = mnist.dataloaders(path)
xb, yb = first(dls.valid)
xb.shapetorch.Size([64, 1, 28, 28])# by default fastai puts batches onto GPU when using DataBlocks
xb, yb = to_cpu(xb), to_cpu(yb)A channel is a single basic color in an image. PyTorch represents an image as a rank-3 tensor with these dimensions:
[channels, rows, columns]
Kernels passed to F.conv2d need to be rank-4 tensors:
[channels_in, features_out, rows, columns]
edge_kernels is missing a dimension currently. We need to tell PyTorch that the number of input channels in the kernel is 1 which we can do by inserting an axis of size 1 (called a unit axis) in the first location.
edge_kernels.shape, edge_kernels.unsqueeze(1).shape(torch.Size([4, 3, 3]), torch.Size([4, 1, 3, 3]))edge_kernels = edge_kernels.unsqueeze(1)batch_features = F.conv2d(xb, edge_kernels)batch_features.shapetorch.Size([64, 4, 26, 26])To become a strong deep learning practitioner, one skill to practice is giving your GPU plenty of work to do at a time. Our manual convolution loop would be millions of times slower.
To avoid losing 2 pixels on each axis, we add padding (commonly zeroes).
Strides and Padding
If we add a kernel of size ks by ks (where ks is an odd number) the necessary padding on each side to keep the same shape is ks//2. An even number of ks would require a different amount of padding on the top/bottom and left/right but in practice we almost never use an even filter size.
stride-2: move over two pixels after each kernel application, useful for decreasing the size of our outputs.
stride-1 convolutions are useful for adding layers without changing the output size.
The most common kernel size in practice is 3x3 and the most common padding is 1.
The general formula for output size given input image dimension n, padding pad, stride and kernel size ks:
(n + 2*pad - ks) // stride + 1
So for a 5x5 image with a 3x3 kernel, stride-2 and 1 pixel of padding:
(5 + 2 * 1 - 3) // 2 + 1 = 4/2 + 1 = 3
When looking at convolution as a matrix multiplication, it has two properties:
The zeros in the matrix are untrainable. They stay 0 throughout the optimization process.
Some of the weights are equal and while they are trainable (i.e. changeable), they must remain equal. These are called shared weights.
Our First Convolutional Neural Network
There is no reason to believe that some particular edge filters are the most useful kernels for image recognition. We don’t have a good idea for how to manually construct lower layer filters (of which later layer convolution kernels become complex transformations). Have the model learn the values of the kernels. When we use convolutions instead of (or in addition to) regular linear layers we create a convolutional neural network (CNN).
simple_net = nn.Sequential(
nn.Linear(28*28, 30),
nn.ReLU(),
nn.Linear(30, 1)
)simple_netSequential(
(0): Linear(in_features=784, out_features=30, bias=True)
(1): ReLU()
(2): Linear(in_features=30, out_features=1, bias=True)
)Use convolutional layers instead of linear.
broken_cnn = sequential(
nn.Conv2d(1, 30, kernel_size=3, padding=1),
nn.ReLU(),
nn.Conv2d(30, 1, kernel_size=3, padding=1)
)We don’t need to specify 28*28 as the input size because the convolution is applied over each pixel automatically. The weights depend only on the number of input and output channels and the kernel size.
xb.shapetorch.Size([64, 1, 28, 28])broken_cnn(xb).shapetorch.Size([64, 1, 28, 28])nn.Conv2d(1, 30, kernel_size=3, padding=1)(xb).shapetorch.Size([64, 30, 28, 28])We can perform enough stride-2 convolutions to get this down to a single value for classification. 28x28 -> 14x14 -> 7x7 -> 4x4 -> 2x2 -> 1x1.
def conv(ni, nf, ks=3, act=True):
res = nn.Conv2d(ni, nf, stride=2, kernel_size=ks, padding=ks//2)
if act: res = nn.Sequential(res, nn.ReLU())
return resWhen using stride-2, increase the number of features at the same time because we are decreasing the number of activations by 4 (we don’t want to decrease the capacity of a layer by too much at a time).
simple_cnn = sequential(
conv(1, 4), # 14 x 14
conv(4, 8), # 7x7
conv(8, 16), # 4x4
conv(16,32), # 2x2
conv(32,2,act=False), #1x1
Flatten()
)simple_cnn(xb).shapetorch.Size([64, 2])conv(1,4)(xb).shapetorch.Size([64, 4, 14, 14])conv(4, 8)(
conv(1,4)(xb)
).shapetorch.Size([64, 8, 7, 7])conv(8, 16)(
conv(4, 8)(
conv(1,4)(xb))).shapetorch.Size([64, 16, 4, 4])conv(16,32)(
conv(8, 16)(
conv(4, 8)(
conv(1,4)(xb)))).shapetorch.Size([64, 32, 2, 2])conv(32, 2, act=False)(
conv(16,32)(
conv(8, 16)(
conv(4, 8)(
conv(1,4)(xb))))).shapetorch.Size([64, 2, 1, 1])Flatten()(
conv(32, 2, act=False)(
conv(16,32)(
conv(8, 16)(
conv(4, 8)(
conv(1,4)(xb)))))
).shapetorch.Size([64, 2])# create our Learner
learn = Learner(dls, simple_cnn, loss_func=F.cross_entropy, metrics=accuracy)learn.summary()Sequential (Input shape: 64 x 1 x 28 x 28)
============================================================================
Layer (type) Output Shape Param # Trainable
============================================================================
64 x 4 x 14 x 14
Conv2d 40 True
ReLU
____________________________________________________________________________
64 x 8 x 7 x 7
Conv2d 296 True
ReLU
____________________________________________________________________________
64 x 16 x 4 x 4
Conv2d 1168 True
ReLU
____________________________________________________________________________
64 x 32 x 2 x 2
Conv2d 4640 True
ReLU
____________________________________________________________________________
64 x 2 x 1 x 1
Conv2d 578 True
____________________________________________________________________________
64 x 2
Flatten
____________________________________________________________________________
Total params: 6,722
Total trainable params: 6,722
Total non-trainable params: 0
Optimizer used: <function Adam at 0x790bb9f92830>
Loss function: <function cross_entropy at 0x790c7f74e950>
Callbacks:
- TrainEvalCallback
- CastToTensor
- Recorder
- ProgressCallbackFlatten is like PyTorch’s squeeze but as a Module.
Let’s train! Since this is a deeper network than we’ve built from scratch before we’ll use a lower learning rate and more epochs:
learn.fit_one_cycle(2, 0.01)| epoch | train_loss | valid_loss | accuracy | time |
|---|---|---|---|---|
| 0 | 0.058796 | 0.036284 | 0.988714 | 00:28 |
| 1 | 0.022334 | 0.025466 | 0.991168 | 00:22 |
/usr/local/lib/python3.10/dist-packages/torch/nn/modules/conv.py:456: UserWarning: Plan failed with a cudnnException: CUDNN_BACKEND_EXECUTION_PLAN_DESCRIPTOR: cudnnFinalize Descriptor Failed cudnn_status: CUDNN_STATUS_NOT_SUPPORTED (Triggered internally at ../aten/src/ATen/native/cudnn/Conv_v8.cpp:919.)
return F.conv2d(input, weight, bias, self.stride,
/usr/local/lib/python3.10/dist-packages/torch/autograd/graph.py:744: UserWarning: Plan failed with a cudnnException: CUDNN_BACKEND_EXECUTION_PLAN_DESCRIPTOR: cudnnFinalize Descriptor Failed cudnn_status: CUDNN_STATUS_NOT_SUPPORTED (Triggered internally at ../aten/src/ATen/native/cudnn/Conv_v8.cpp:919.)
return Variable._execution_engine.run_backward( # Calls into the C++ engine to run the backward passUnderstanding Convolution Arithmetic
Input size is 64x1x28x28 which is batch, channel, height, width.
First layer of the model:
m = learn.model[0]m # 1 input channel, 4 output channels, 3x3 kernelSequential(
(0): Conv2d(1, 4, kernel_size=(3, 3), stride=(2, 2), padding=(1, 1))
(1): ReLU()
)# layer 1 weights
m[0].weight.shapetorch.Size([4, 1, 3, 3])4 x 1 x 3 x 3 = 36 weights, but learn.summary says this layer has 40 params. What are the other 4? Bias!
m[0].bias.shape # one bias for each channeltorch.Size([4])learn.model[1]Sequential(
(0): Conv2d(4, 8, kernel_size=(3, 3), stride=(2, 2), padding=(1, 1))
(1): ReLU()
)learn.model[1][0].weight.shapetorch.Size([8, 4, 3, 3])8*4*3*3288288 params + 8 bias values = 296 params.
Ignoring bias, this layer has 14 x 14 = 196 locations multiplied by 288 parameters resulting in 56_448 multiplications.
The next layer:
learn.model[2]Sequential(
(0): Conv2d(8, 16, kernel_size=(3, 3), stride=(2, 2), padding=(1, 1))
(1): ReLU()
)learn.model[2][0].weight.shapetorch.Size([16, 8, 3, 3])16*8*3*31152Will have 7 x 7 x 1152 = 56_448 multiplications. We halved the grid size from 14x14 to 7x7 (using stride-2) and doubled the number of filters from 8 to 16.
7*7*115256448If we left the number of channels the same in each stride-2 layer, the amount of computation being done in the net would get less and less as it gets deeper, but we know that deeper layers have to compute semantically rich features (such as eyes or furs) so we wouldn’t expect that doing less computation would make sense.
Receptive Fields
The receptive field is the area of an image that is involved in the calculation of a layer. The deeper we are in the network (the more stride-2 convs we have before a layer) the larger the receptive field for an activation in that layer is. A larger receptive field means that a large amount of the input image is used to calculate each activation in that layer. We’d expect that we’d need more weights for each of the deeper layer’s richer features to handle this increased complexity—which is why with stride-2 we increase the number of features in each deeper layer (since the input size decreases).
Color Images
A color picture is a rank-3 tensor.
im = image2tensor(Image.open('/content/grizzly.jpg'))
im.shapetorch.Size([3, 1000, 846])The first axis contains red, green and blue channels
_,axs = subplots(1,3)
for bear,ax,color in zip(im,axs,('Reds', 'Greens', 'Blues')):
show_image(255-bear, ax=ax, cmap=color)In one sliding window we have a certain number of channels and we need as many filters (we don’t use the same kernel for all the channels). kernel size: ch_in x 3 x 3. We sum the results for all three channel window x filter multiplications to produce a single number for each grid location for each ch_out output feature. The result of our convolutional layer: ch_out x ch_in x ks x ks.
There are as many biases as we have kernels. The bias is a vector of size ch_out.
Changing the encoding of colors won’t make any difference to your model results, as long as you don’t lose information in the transformation (transforming to B/W is a bad idea as it loses color information while converting to HSV generally won’t make a difference).
Improving Training Stability
Create a 10-digit classifier.
def conv(ni, nf, ks=3, act=True):
res = nn.Conv2d(ni, nf, stride=2, kernel_size=ks, padding=ks//2)
if act: res = nn.Sequential(res, nn.ReLU())
return respath = untar_data(URLs.MNIST)
path.ls()(#2) [Path('/root/.fastai/data/mnist_png/testing'),Path('/root/.fastai/data/mnist_png/training')]# create a function to change dls params
def get_dls(bs=64):
return DataBlock(
blocks=(ImageBlock(cls=PILImageBW), CategoryBlock),
get_items=get_image_files,
splitter=GrandparentSplitter('training', 'testing'),
get_y=parent_label,
batch_tfms=Normalize()
).dataloaders(path, bs=bs)dls = get_dls()pd.Series([el.parent.name for el in dls.valid.items]).sort_values().unique()array(['0', '1', '2', '3', '4', '5', '6', '7', '8', '9'], dtype=object)A Simple Baseline
Use a similar CNN as before but with more activations (more numbers to differentiate = we’ll likely need more filters).
We generally want to double the number of filters each time we have a stride-2 layer. One way to increase the number of filters throughout our network is to double the number of activations in the first layer—then every layer after that will end up twice as big as in the previous version.
Neural networks will create useful features only if they’re forced to do so—that is, if the number of outputs from an operation is significantly smaller than the number of inputs. If we have a 3x3 kernel, the number of inputs is 9. If we have 8 filters, we’ll be using 9 numbers (3x3) to calculate 8 numbers. It isn’t learning much at all (input and output size is the same). To fix this, use a larger kernel for the first layer, 5x5, so that 25 values are used to learn 8 values (one for each of the 8 filters) at each location.
def simple_cnn():
return sequential(
conv(1, 8, ks=5), # 14x14
conv(8, 16), # 7x7
conv(16, 32), # 4x4
conv(32, 64), # 2x2
conv(64, 10, act=False), # 1x1
Flatten()
)xb, yb = first(dls.valid)
xb, yb = to_cpu(xb), to_cpu(yb)conv(1, 8, ks=5)(xb).shapetorch.Size([64, 8, 14, 14])We can look inside of our models while they’re training with the Activation Stats callback which records the mean, standard deviation and histogram of activations of every trainable layer.
from fastai.callback.hook import *def fit(epochs=1):
learn = Learner(dls, simple_cnn(), loss_func=F.cross_entropy, metrics=accuracy, cbs=ActivationStats(with_hist=True))
learn.fit(epochs, 0.06)
return learnlearn = fit()| epoch | train_loss | valid_loss | accuracy | time |
|---|---|---|---|---|
| 0 | 2.307114 | 2.306540 | 0.101000 | 01:07 |
That didn’t train well, let’s find out why.
learn.summary()Sequential (Input shape: 64 x 1 x 28 x 28)
============================================================================
Layer (type) Output Shape Param # Trainable
============================================================================
64 x 8 x 14 x 14
Conv2d 208 True
ReLU
____________________________________________________________________________
64 x 16 x 7 x 7
Conv2d 1168 True
ReLU
____________________________________________________________________________
64 x 32 x 4 x 4
Conv2d 4640 True
ReLU
____________________________________________________________________________
64 x 64 x 2 x 2
Conv2d 18496 True
ReLU
____________________________________________________________________________
64 x 10 x 1 x 1
Conv2d 5770 True
____________________________________________________________________________
64 x 10
Flatten
____________________________________________________________________________
Total params: 30,282
Total trainable params: 30,282
Total non-trainable params: 0
Optimizer used: <function Adam at 0x7d6f11cb0700>
Loss function: <function cross_entropy at 0x7d6fd5b369e0>
Model unfrozen
Callbacks:
- ActivationStats
- TrainEvalCallback
- CastToTensor
- Recorder
- ProgressCallbackGenerally our model should have a consistent, or at least smooth, mean and standard deviation of layer activations during training. Activations near zero are problematic because that means the model is doing nothing and that carries over to the next layer.
The problem, as expected, gets worse by the end of the network with nearly 100% of the activations close to 0.
l_stats = learn.activation_stats.layer_stats(0)len(l_stats[0])937len(dls.train.items) / 64937.5Note: 937 = number of batches in training set, so the mean activation is across the batch (as is standard deviation, and % near zero).
Increase Batch Size
One way to make training more stable is to increase the batch size. Large batches have gradients that are more accurate since they’re calculated from more data with the downside of fewer opportunities to update weights (fewer batches per epoch).
dls = get_dls(512)learn = fit()| epoch | train_loss | valid_loss | accuracy | time |
|---|---|---|---|---|
| 0 | 0.398756 | 0.203404 | 0.935500 | 01:01 |
Even though the accuracy is higher, most of the activations are near zero.
1cycle Training
Our initial weights are not well suited to the task we’re trying to solve. Starting with a large learning rate may diverge the training from the start. We don’t want to end with a high learning rate either because we don’t want to skip over the minimum. We should change learning rate from low, to high, and then back to low again. Leslie Smith developed this idea—a schedule where in the first phase the learning rate grows from the minimum value to the maximum value (warmup), and then decreases back to minimum (annealing)—1cycle training which allows for higher learning rates (trains faster, “super-convergence” and overfits less by skipping over the sharp local minima).
A model that generalizes well is one whose loss would not change very much if you changed the input by a small amount (I think one way to think about that is a smooth loss surface—no quick or sudden sharp changes). If a model trains with a large learning rate and finds a good loss when doing so (i.e. a loss that doesn’t change very much) it will generalize well.
Once we have found a nice smooth area for our parameters, we want to find the very best part of that area so we bring learning rates down again.
momentum: the optimizer takes a step not only in the direction of the gradients, but also that continues in the direction of previous steps. Momentum varies in the opposite direction of the learning rate: high learning rates -> less momentum (Leslie Smith, AGAIN!).
def fit(epochs=1, lr=0.06):
learn = Learner(dls, simple_cnn(), loss_func=F.cross_entropy, metrics=accuracy, cbs=ActivationStats(with_hist=True))
learn.fit_one_cycle(epochs, lr)
return learnlearn = fit()/usr/local/lib/python3.10/dist-packages/fastai/callback/core.py:69: UserWarning: You are shadowing an attribute (modules) that exists in the learner. Use `self.learn.modules` to avoid this
warn(f"You are shadowing an attribute ({name}) that exists in the learner. Use `self.learn.{name}` to avoid this")| epoch | train_loss | valid_loss | accuracy | time |
|---|---|---|---|---|
| 0 | 0.196365 | 0.070784 | 0.977500 | 01:11 |
% near zero is lower for some batches but still overall high.
fastai implements cosine annealing in the learning rate scheduler.
fit_one_cycle parameters:
lr_max: the highest learning rate to be used (can also be a list for each layer group or a Python slice object containing the first and last layer group learning rates)
div: How much to divide lr_max by to get the starting learning rate.
div_final: how much to divide lr_max by to get the ending learning rate.
pct_start: what percentages of the batches to use for the warmup
moms: a tuple (mom1,mom2,mom3) where mom1 is the initial momentum, mom2 is the minimum momentum, and mom3 is the final momentum.
The axes on the graph is the number of batches (60_000 training images / 512 images per batch = 117 batches).
This is a classic picture of “bad training”. White = zero activations. Black at the bottom left is near-zero activations. The near-zero activations exponentially increase and then collapse almost like the training is starting over. We see this increase and collapse again a few times before the distribution is spread throughout the range. Starting the training smooth from the start can be achieved with batch normalization.
Batch Normalization
We need to fix the initial large percentage of near-zero activations and then try to maintain a good distribution of activations throughout training.
From the Batch Normalization paper (2015, Ioffe and Szegedy):
internal covariate shift: distribution of each layer’s inputs changes during training as the parameters of the previous layers change which slows down the training (lower learning rates required) and requires careful parameter initialization.
Making normalization a part of the model architecture and performing the normalization for each training mini-batch. Batch Normalization allows us to use much higher learning rates and be less careful about initialization.
batchnorm: taking an average of the mean and standard deviations of the activations of a layer and using those to normalize the activations. The network will want to make some activations really high to make accurate predictions so there are two learnable parameters gamma and beta. After normalizing the activations to get some new activation vector y a batchnorm layer returns gamma*y + beta.
Our activations can have any mean and variance independent from the mean and standard deviation of the results of the previous layer. During training we use mean and std of the batch to normalize the data, during validation we use a running mean aof the stats calculated during training.
# add batchnorm
def conv(ni, nf, ks=3, act=True):
layers = [nn.Conv2d(ni, nf, stride=2, kernel_size=ks, padding=ks//2)]
layers.append(nn.BatchNorm2d(nf))
if act: layers.append(nn.ReLU())
return nn.Sequential(*layers)learn = fit()/usr/local/lib/python3.10/dist-packages/fastai/callback/core.py:69: UserWarning: You are shadowing an attribute (modules) that exists in the learner. Use `self.learn.modules` to avoid this
warn(f"You are shadowing an attribute ({name}) that exists in the learner. Use `self.learn.{name}` to avoid this")| epoch | train_loss | valid_loss | accuracy | time |
|---|---|---|---|---|
| 0 | 0.126032 | 0.055595 | 0.987400 | 01:12 |
That’s what we hope to see—a smooth development of activations with no collapses. We see batchnorm in nearly all modern neural networks.
We haven’t as yet seen rigorous analysis of what’s going on here, but most researchers believe that the reason models containing batch norm layers generalize better is that the normalization adds some extra randomness to the training process. Each mini-batch will have a somewhat different mean and std than other mini-batches. The activations will be normalized by different values each time. The model will learn to become robust to these variations to make accurate predictions. Adding additional randomization to the training process often helps.
learn = fit(5, lr=0.1)/usr/local/lib/python3.10/dist-packages/fastai/callback/core.py:69: UserWarning: You are shadowing an attribute (modules) that exists in the learner. Use `self.learn.modules` to avoid this
warn(f"You are shadowing an attribute ({name}) that exists in the learner. Use `self.learn.{name}` to avoid this")| epoch | train_loss | valid_loss | accuracy | time |
|---|---|---|---|---|
| 0 | 0.187965 | 0.117173 | 0.963600 | 01:09 |
| 1 | 0.079750 | 0.052391 | 0.983100 | 01:08 |
| 2 | 0.052439 | 0.048151 | 0.985200 | 01:03 |
| 3 | 0.032153 | 0.032204 | 0.989200 | 01:10 |
| 4 | 0.017457 | 0.024827 | 0.992300 | 01:04 |
Conclusion
Convolutions are matrix multiplications with two constraints—some elements are always zero and som elements are tied (forced to be equal). These constraints enforce a certain pattern of connectivity, and allow us to use fewer parameters without sacrificing ability to represent complex visual features. We can train deeper models faster with less overfitting. Regular linear layers are called fully connected. Batch norm helps regularize training and makes it smoother.
Questionnaire
1. What is a feature?
A visually distinctive attribute of an image.
2. Write out the convolutional kernel matrix for a top edge detector.
| -1 | -1 | -1 |
| 0 | 0 | 0 |
| 1 | 1 | 1 |
3. Write out the mathematical operation applied by a 3x3 kernel to a single pixel in an image.
Assuming that this question pertains to a 3x3 grid in the image, suppose we apply the kernel in #2 to the following 3x3 grid:
| a1 | a2 | a3 |
| a4 | a5 | a6 |
| a7 | a8 | a9 |
The result is the equation:
-a1 - a2 - a3 + a7 + a8 + a9
4. What is the value of a convolutional kernel applied to a 3x3 matrix of zeros?
0
5. What is padding?
Adding additional pixels around the border of the image to avoid skipping two pixels on each axis. With padding, instead of the kernel fitting fully inside the image at the edges, a portion of the kernel is on the padding pixels.
6. What is stride?
The number of pixels by which the kernel moves or slides over the image. Stride-2 means the kernel moves over by two pixels (skipping one pixel).
7. Create a nested list comprehension to complete any task that you choose.
[(i, j, k) for i in range(3) for j in range(4) for k in range(2)][(0, 0, 0),
(0, 0, 1),
(0, 1, 0),
(0, 1, 1),
(0, 2, 0),
(0, 2, 1),
(0, 3, 0),
(0, 3, 1),
(1, 0, 0),
(1, 0, 1),
(1, 1, 0),
(1, 1, 1),
(1, 2, 0),
(1, 2, 1),
(1, 3, 0),
(1, 3, 1),
(2, 0, 0),
(2, 0, 1),
(2, 1, 0),
(2, 1, 1),
(2, 2, 0),
(2, 2, 1),
(2, 3, 0),
(2, 3, 1)][[[i, j, k] for i in ['i1', 'i2', 'i3']] for j in ['j1', 'j2'] for k in ['k1', 'k2']][[['i1', 'j1', 'k1'], ['i2', 'j1', 'k1'], ['i3', 'j1', 'k1']],
[['i1', 'j1', 'k2'], ['i2', 'j1', 'k2'], ['i3', 'j1', 'k2']],
[['i1', 'j2', 'k1'], ['i2', 'j2', 'k1'], ['i3', 'j2', 'k1']],
[['i1', 'j2', 'k2'], ['i2', 'j2', 'k2'], ['i3', 'j2', 'k2']]]8. What are the shapes of the input and weight parameters to PyTorch’s 2D convolution?
input: (minibatch, in_channels, lH, lW) weight: filters of shape (out_channels, in_channels, kH, kW)
9. What is a channel?
A single basic color in an image.
10. What is the relationship between a convolution and a matrix multiplication?
A convolution is a matrix multiplication with two constraints:
- some elements in the kernel matrix always stay 0.
- some elements in that matrix are always equal to each other.
11. What is a convolutional neural network?
A neural network with non-linearity function sandwiched between convolutions. In other words, replacing the fully-connected (linear) layers in a neural network with convolutions.
12. What is the benefit of refactoring parts of your neural network definition?
Less likely to get errors due to inconsistencies in architecutre. More obvious to reader which parts of your layers are actually changing.
13. What is Flatten? Where does it need to be included in the MNIS CNN? Why?
A fastai/PyTorch layer that flattens the input to a single dimension, used at the end of the model. In our case, it removes the final 1x1 convolution dimensions.
x = torch.ones(2, 1, 1)
x.shapetorch.Size([2, 1, 1])xtensor([[[1.]],
[[1.]]])x[1], x[1][0], x[1][0][0](tensor([[1.]]), tensor([1.]), tensor(1.))x[1].shape, x[1][0].shape, x[1][0][0].shape(torch.Size([1, 1]), torch.Size([1]), torch.Size([]))Flatten()(x).shapetorch.Size([2, 1])Flatten()(x), Flatten()(x)[1], Flatten()(x)[1][0](tensor([[1.],
[1.]]),
tensor([1.]),
tensor(1.))Flatten()(x)[1].shape, Flatten()(x)[1][0].shape(torch.Size([1]), torch.Size([]))14. What does NCHW mean?
N = batch size
C = channels
H = height
W = width
15. Why does the third layer of the MNIST CNN have 7*7*(1168-16) multiplications?
7x7 is the dimension of the resulting filters coming out of the previous convolution (second layer). 1152 (which is 1168 - 16) is the number of non-bias parameters in the third layer, which comes from the fact that the weight in that layers convolution has dimensions 8 x 16 x 3 x 3 (8 inputs, 16 output features and a 3x3 kernel).
8*16*3*3115216. What is a receptive field?
The area of an image that is involved in the calculation of a layer.
17. What is the size of the receptive field of an activation after two stride-2 convolutions? Why?
7x7. The activation in layer 2 is made from a 3x3 receptive field in layer 1. That 3x3 layer 1 area is made up of 7x7 receptive field in layer 0 (the original image).
Let’s focus on the top-most and left-most activation in layer 2. That comes from the top-left-most 3x3 pixels in layer 1. The top-left-most pixel in layer 1 comes from the top-left-most pixel in layer 0. The next pixel to the right in layer 1 comes from a 3x3 grid starting at the the first-row third pixel in layer 0. The next pixel to the right in layer 1 comes from a 3x3 grid starting at the first-row fifth pixel in layer, which covers pixel 5, 6, and 7 in the first row of layer 0 (the original image). In this way, vertically, pixels 1 through 7 in the first column are involved, and the whole 7x7 grid is involved in layer 0 when looking at the whole 3x3 grid in layer 1.
18. Run conv-example.xlsx yourself and experiment with trace precedents
I recreated the whole notebook while following the Lesson 8 video. I also used trace precedents when answering question #17.
19. Have a look at Jeremy’s or Sylvain’s recent Twitter “likes”, and see if you find any interesting resources or ideas there.
Likes are no longer public on Twitter but I have follow a bunch of folks that Jeremy follows.
20. How is a color image represented as a tensor?
A rank-3 tensor (3 channels, height, width).
21. How does a convolution work with a color input?
It applies a different filter to each channel and then sums the results for each pixel.
22. What method can we use to see the data in DataLoaders?
show_batch
23. Why do we double the number of filters after each stride-2 conv?
Since the image reduces in size by half, we double the number of filters so that as deeper layers learn more complex features there’s enough data to learn from.
24. Why do we use a larger kernel in the first conv with MNIST (with simple_cnn)?
If we use a 3x3 kernel to produce 8 filters, that’s 9 inputs producing 8 outputs—the model isn’t learning much. For the model to learn things, the number of inputs should be larger than the number of outputs. So if we use a 5x5 kernel, that’s 25 pixels producing 8 outputs, so the model has to learn useful features.
25. What information does ActivationStats save for each layer?
Mean and standard deviation of activations.
26. How can we access a learner’s callback after training?
Learner.<name of callback> for example the ActivationStats callback is accessed after training with Learner.activation_stats.
27. What are the three statistics plotted by plot_layer_stats? What does the x-axis represent?
Three statistics plotted: mean activations, standard deviation of activations and % of activations near zero. The x-axis represents the batches.
28. Why are activations near zero problematic?
Because they result in the model doing nothing after the computation (multiplying by 0 = 0). Also, the resulting 0-activations result in more 0 activations in the next layer. In this way, the deeper you go, the more the activations are near zero if the early layers have many near-zero activations.
29. What are the upsides and downsides of training with a larger batch size?
Upside: smoother training. Downside: fewer gradient updates (opportunities to “learn”).
30. Why should we avoid using a high learning rate at the start of training?
We will “overshoot” the minimum and the training will diverge (exploding gradeints).
31. What is 1cycle training?
A learning rate schedule where the learning starts starts off small, warms up to a larger value then anneals back down to a smaller value.
32. What are the benefits of training with a high learning rate?
You can train quicker and overfit less (since we skip over sharp local minima).
33. Why do we want to use a low learning rate at the end of training?
Assuming that we have found the minimum, we don’t want to overshoot it so a smaller learning rate takes smaller steps towards the minimum.
34. What is cyclical momentum?
Momentum is “a technique whereby the optimizer takes a stepo not only in the direction of the gradients, but also that continues in the direction of previous steps.” Cyclical momentum is when the momentum is on a schedule going from large, to small to large again (in the case of 1cycle training).
35. What callback tracks hyperparameter values during training (along with other information)?
Recorder
36. What does one column of pixels in the color_dim plot represent?
The activations for one batch.
37. What does “bad training” look like in color_dim? Why?
Cyclical increase and collapse of nonzero activations. This results in near zero activations at the end of training which can lead to poor results.
38. What trainable parameters does a batch normalization layer contain?
gamma and beta where given a vector y of normalized activations, gamma * y + beta is the “learned” normalization returned by batchnorm.
39. What statistics are used to normalize in batch normalization during training? How about during validation?
training: mean and standard deviation of the activations of the batch.
validation: running mean and standard deviations from previous
40. Why do models with batch normalization layers generalize better?
We don’t fully know (at least at the time of writing) but it’s likely because the normalization (including the learned parameters) adds randomness and additional randomness generally helps the model generalize better.