!pip install RAGatouille -qqRecreating the PLAID ColBERTv2 Scoring Pipeline: From Research Code to RAGatouille
from ragatouille import RAGPretrainedModel
import colbert
from fastcore.utils import Path
import json
import torchBackground
This walkthrough reconstructs the PLAID scoring pipeline by tracing code paths in the ColBERT research codebase that reproduce RAGatouille’s verified results. This is a reverse engineering process - I pulled at promising threads (code related to centroids, passage IDs, and scores) and validated my understanding by comparing against RAGatouille’s known-correct outputs.
Here’s my video walkthrough of the code in this notebook:
RAGatouille Results
In this notebook, the gold truth scores for the documents given a query are determined by the RAGatouille library. I create a query (What is Python?) and a simple set of documents where one document is the obvious right answer (Python is a programming language. It is easy to learn) , one is a hard negative in that it’s about Python (Python was created by Guido van Rossum in 1991) and one is a easier negative as it’s related to the programming but not about Python (Java is a popular coding language used in many applications).
RAG = RAGPretrainedModel.from_pretrained("colbert-ir/colbertv2.0")q = "What is Python?"
q'What is Python?'documents = [
"Python is a programming language. It is easy to learn",
"Java is a popular coding language used in many applications",
"Python was created by Guido van Rossum in 1991"
]
documents['Python is a programming language. It is easy to learn',
'Java is a popular coding language used in many applications',
'Python was created by Guido van Rossum in 1991']index_path = RAG.index(index_name="toy_example", collection=documents)index_path'.ragatouille/colbert/indexes/toy_example'results = RAG.search(q)
resultsWARNING: k value is larger than the number of documents in the index! Lowering k to 3...[{'content': 'Python is a programming language. It is easy to learn',
'score': 27.6875,
'rank': 1,
'document_id': '8aa5aade-10d5-4144-b634-c7866578b43c',
'passage_id': 0},
{'content': 'Python was created by Guido van Rossum in 1991',
'score': 22.28125,
'rank': 2,
'document_id': '12352328-9bb1-4a51-896e-a002d3548adc',
'passage_id': 2},
{'content': 'Java is a popular coding language used in many applications',
'score': 13.953125,
'rank': 3,
'document_id': '1fe9788e-ccec-4b9e-a004-14acc657915e',
'passage_id': 1}]Note the score and passage_id—these are values I’ll continuously reference throughout my walkthrough:
passage_id |
score |
passage text |
|---|---|---|
| 0 | 27.6875 | “Python is a programming language. It is easy to learn” |
| 2 | 22.28125 | “Python was created by Guido van Rossum in 1991” |
| 1 | 13.953125 | “Java is a popular coding language used in many applications” |
Where to Start?
Starting at the top—the model in play: of type ColBERT
m = RAG.model
m<ragatouille.models.colbert.ColBERT at 0x7d0a4cc14670>And its index—of type PLAIDModelIndex.
index = m.model_index
index<ragatouille.models.index.PLAIDModelIndex at 0x7d0bd8bb7e80>Inside the source code for PLAIDModelIndex the most promising method seemed be the _search method, which contains the following line:
return self.searcher.search(query, k=k, pids=pids)This contained three things I recognized: the query, the top k value and the passage IDs pids.
index.searcher<colbert.searcher.Searcher at 0x7d0a4cdc6530>The Searcher Class
I couldn’t find the Searcher in RAGAtouille’s codebase as it was imported from colbert. Thankfully, installing RAGatouille gives you access to this library!
colbert.Searchercolbert.searcher.Searcher
def __init__(index, checkpoint=None, collection=None, config=None, index_root=None, verbose: int=3)
<no docstring>
The Searcher takes as a required argument an index path—which we have!
searcher = colbert.Searcher(index='toy_example')[Dec 24, 15:59:52] #> Loading codec...
[Dec 24, 15:59:52] #> Loading IVF...
[Dec 24, 15:59:52] #> Loading doclens...100%|██████████| 1/1 [00:00<00:00, 4315.13it/s][Dec 24, 15:59:52] #> Loading codes and residuals...
100%|██████████| 1/1 [00:00<00:00, 454.67it/s]Notice that it loads the codec, IVF and doclens, all things we’ll look at throughout this notebook. Looking inside the Searcher.search method (which was called in the PLAIDModelIndex._search method) I see the following:
def search(self, text: str, k=10, filter_fn=None, full_length_search=False, pids=None):
Q = self.encode(text, full_length_search=full_length_search)
return self.dense_search(Q, k, filter_fn=filter_fn, pids=pids)This is encoding the text into Q. Looks promising. I’ll see what that gets me:
Q = searcher.encode(q)
Q.shapetorch.Size([1, 32, 128])Looks good! It has 32 tokens, each with a 128-dimension encoding.
Searcher.search returns the output of Searcher.dense_search, and the Searcher.dense_search method looks very promising. It takes queries Q and passages IDs and returns passage IDs and scores.
pids, scores = self.ranker.rank(self.config, Q, filter_fn=filter_fn, pids=pids)
return pids[:k], list(range(1, k+1)), scores[:k]searcher.dense_searchcolbert.searcher.Searcher.dense_search
def dense_search(Q: torch.Tensor, k=10, filter_fn=None, pids=None)
<no docstring>
searcher.dense_search(Q)([0], [1, 2, 3, 4, 5, 6, 7, 8, 9, 10], [27.6875])Excellent!! The first value is pids[:k], which I understand to be the passage IDs corresponding to the top-k results. In this case it’s just 1 passage ID, 0, the first passage (“Python is a programming language. It is easy to learn”). The second value is list(range(1,k+1)) which is just a list from 1 to k. The final value is scores[:k] which is score corresponding to the top-k values. In this case it’s just one score, but an important one in our journey, as it is the same as RAGatouille for this passage (27.6875) !
results[0]{'content': 'Python is a programming language. It is easy to learn',
'score': 27.6875,
'rank': 1,
'document_id': '8aa5aade-10d5-4144-b634-c7866578b43c',
'passage_id': 0}This is incredibly exciting, but I’m only getting 1 score instead of 3. Looking more closely at dense_search I see that the value of k determines the value of config.ncells:
if k <= 10:
if self.config.ncells is None:
self.configure(ncells=1)
if self.config.centroid_score_threshold is None:
self.configure(centroid_score_threshold=0.5)
if self.config.ndocs is None:
self.configure(ndocs=256)Afterwhich dense_search calls:
pids, scores = self.ranker.rank(self.config, Q, filter_fn=filter_fn, pids=pids)I’ll look at Searcher.ranker.rank next.
Searcher.ranker.rank
searcher.ranker.rankcolbert.search.index_storage.IndexScorer.rank
def rank(config, Q, filter_fn=None, pids=None)
<no docstring>
The first parameter, config, is found in the Searcher:
searcher.configColBERTConfig(query_token_id='[unused0]', doc_token_id='[unused1]', query_token='[Q]', doc_token='[D]', ncells=1, centroid_score_threshold=0.5, ndocs=256, load_index_with_mmap=False, index_path=None, index_bsize=32, nbits=4, kmeans_niters=20, resume=False, similarity='cosine', bsize=64, accumsteps=1, lr=1e-05, maxsteps=400000, save_every=None, warmup=20000, warmup_bert=None, relu=False, nway=64, use_ib_negatives=True, reranker=False, distillation_alpha=1.0, ignore_scores=False, model_name=None, query_maxlen=32, attend_to_mask_tokens=False, interaction='colbert', dim=128, doc_maxlen=256, mask_punctuation=True, checkpoint='colbert-ir/colbertv2.0', triples='/future/u/okhattab/root/unit/experiments/2021.10/downstream.distillation.round2.2_score/round2.nway6.cosine.ib/examples.64.json', collection=<colbert.data.collection.Collection object at 0x7d0a4cc052d0>, queries='/future/u/okhattab/data/MSMARCO/queries.train.tsv', index_name='toy_example', overwrite=False, root='.ragatouille/', experiment='colbert', index_root=None, name='2024-12/24/15.52.48', rank=0, nranks=1, amp=True, gpus=1, avoid_fork_if_possible=False)ncells is 1.
searcher.config.ncells1From my previous amblings through the codebase, and which will see later on, I learned that ncells is synonymous with the \(n_{probe}\) parameter in the ColBERTv2 and PLAID ColBERTv2 papers (i.e. the number of centroids closest to each query token). In the papers they use values of 1, 4, and 8. I’ll pick a value of 4.
searcher.config.configure(ncells=4)
searcher.config.ncells4I’ll now pass config to Searcher.ranker.rank along with my encoded query Q:
searcher.ranker.rank(config=searcher.config, Q=Q)([0, 2, 1], [27.6875, 22.28125, 13.953125])Major success!! I now see three passage IDs and their corresponding scores, an exact match with RAGatouille’s results.
results[{'content': 'Python is a programming language. It is easy to learn',
'score': 27.6875,
'rank': 1,
'document_id': '8aa5aade-10d5-4144-b634-c7866578b43c',
'passage_id': 0},
{'content': 'Python was created by Guido van Rossum in 1991',
'score': 22.28125,
'rank': 2,
'document_id': '12352328-9bb1-4a51-896e-a002d3548adc',
'passage_id': 2},
{'content': 'Java is a popular coding language used in many applications',
'score': 13.953125,
'rank': 3,
'document_id': '1fe9788e-ccec-4b9e-a004-14acc657915e',
'passage_id': 1}]At this point I felt confident in the threads I was pulling and could now dig deeper and start recreating each stage of the PLAID scoring pipeline, starting with Stage 1.
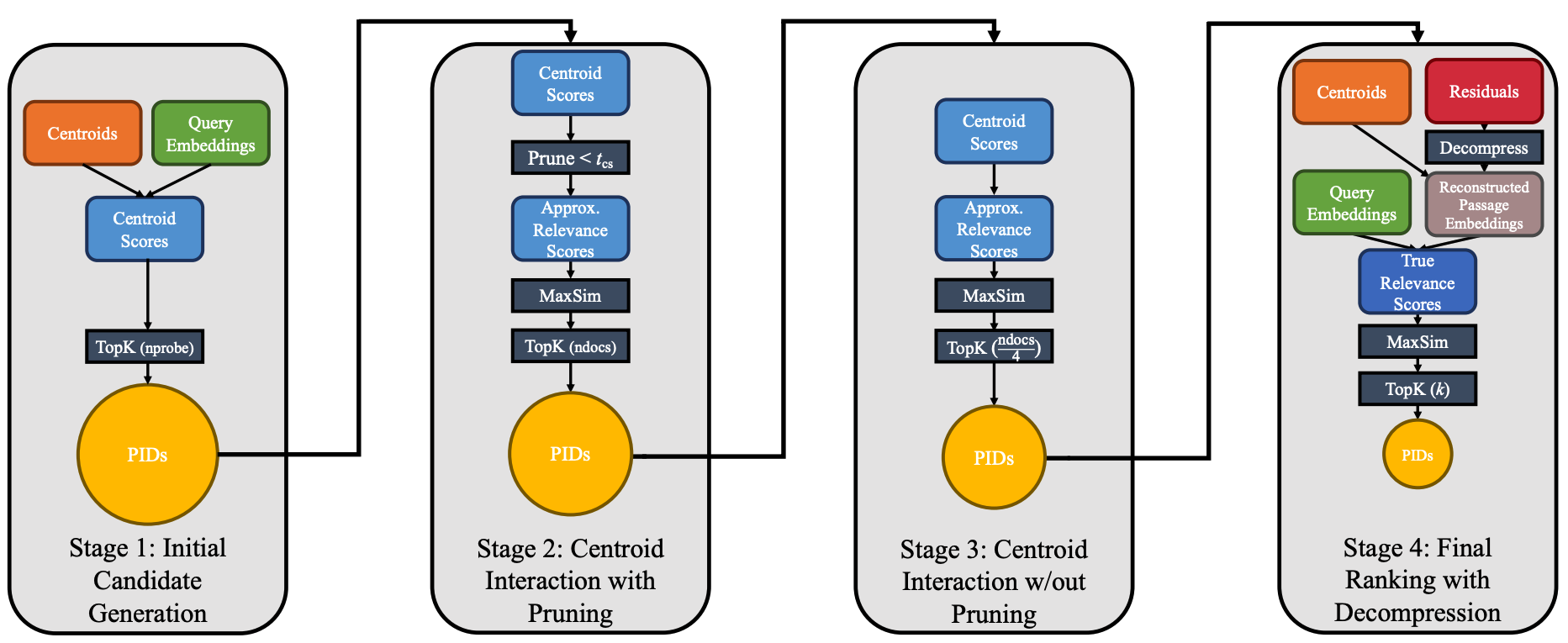
Stage 1: Initial Candidate Generation
In Stage 1, we retrieve the passage IDs corresponding to the ncells centroid IDs neareest to each of the query tokens. I have set ncells to 4 and have 32 query tokens so we’re dealing with a maximum of 4 x 32 = 128 centroid IDs.
The first promising line in Searcher.ranker.rank is the call to retrieve:
if pids is None:
pids, centroid_scores = self.retrieve(config, Q)Searcher.ranker.retrieve
searcher.ranker.retrievecolbert.search.index_storage.IndexScorer.retrieve
def retrieve(config, Q)
<no docstring>
pids, centroid_scores = searcher.ranker.retrieve(searcher.config, Q)
pids, centroid_scores.shape(tensor([0, 1, 2], device='cuda:0', dtype=torch.int32), torch.Size([64, 32]))This is where I start to get really excited. I’m seeing abstract concepts in a research paper come to life! pids is now familiar—the three indexes 0, 1, and 2. What’s more interesting is centroid_scores which has 64 rows and 32 columns. We know from the PLAID paper that the MaxSim scores between centroids and query tokens is matrix with number of rows being the number of centroids and the number of columns being the number of tokens.
Looking inside of Searcher.ranker.retrieve we see that it calls Searcher.ranker.generate_candidates:
pids, centroid_scores = self.generate_candidates(config, Q)generate_candidates
searcher.ranker.generate_candidatescolbert.search.candidate_generation.CandidateGeneration.generate_candidates
def generate_candidates(config, Q)
<no docstring>
This will only be a brief pit stop. There are three lines of interest:
Q = Q.squeeze(0)
Q = Q.cuda().half()
pids, centroid_scores = self.generate_candidate_pids(Q, ncells)Q = Q.squeeze(0)
Q.shapetorch.Size([32, 128])Q = Q.cuda().half()searcher.ranker.generate_candidatescolbert.search.candidate_generation.CandidateGeneration.generate_candidates
def generate_candidates(config, Q)
<no docstring>
cells, scores = searcher.ranker.generate_candidates(searcher.config, Q)
cells.shape, scores.shape(torch.Size([3]), torch.Size([64, 32]))There’s that 64 x 32 shape again.
cellstensor([0, 1, 2], device='cuda:0', dtype=torch.int32)I’m not entirely sure what cells is (I’m tempted to say it’s our passage IDs based on the values). Let’s look at get_candidate_pids first:
generate_candidate_pids
Another quick stop, we see the following two very interesting line:
cells, scores = self.get_cells(Q, ncells)
pids, cell_lengths = self.ivf.lookup(cells)From reading the paper, I know that in Stage 1 we get the centroid IDs that are close to the query tokens, which I think is what get_cells does. I also know that the PLAID index stores a mapping between passage IDs and centroid IDs, which is what I think ivf.lookup is looking up!
get_cells
def get_cells(self, Q, ncells):
scores = (self.codec.centroids @ Q.T)
if ncells == 1:
cells = scores.argmax(dim=0, keepdim=True).permute(1, 0)
else:
cells = scores.topk(ncells, dim=0, sorted=False).indices.permute(1, 0) # (32, ncells)
cells = cells.flatten().contiguous() # (32 * ncells,)
cells = cells.unique(sorted=False)
return cells, scoresThe first line is critical: self.codec.centroids @ Q.T is almost verbatim the matrix multiplication formula in the paper. This confirms that the 64 x 32 shape of scores is number of centroids x number of query tokens!
searcher.ranker.codec.centroids.shapetorch.Size([64, 128])There are indeed 64 centroids, each of them with 128 dimensions. So cool to see!!
_scores = (searcher.ranker.codec.centroids @ Q.T)
_scores.shapetorch.Size([64, 32])(scores == _scores).float().mean()tensor(1., device='cuda:0')The next line of interest is:
cells = scores.topk(ncells, dim=0, sorted=False).indices.permute(1, 0) # (32, ncells)scores.shapetorch.Size([64, 32])scorestensor([[ 0.0879, 0.0498, 0.0136, ..., 0.0586, 0.0564, 0.0699],
[ 0.0798, -0.0043, 0.0223, ..., -0.0271, -0.0166, -0.0172],
[ 0.2053, 0.0300, 0.1144, ..., 0.0100, 0.0226, 0.0177],
...,
[ 0.4587, 0.9458, 0.1954, ..., 0.9507, 0.9482, 0.9482],
[ 0.0000, 0.0000, 0.0000, ..., 0.0000, 0.0000, 0.0000],
[ 0.0000, 0.0000, 0.0000, ..., 0.0000, 0.0000, 0.0000]],
device='cuda:0', dtype=torch.float16)scores.topk seems to return the scores corresponding to the top-4 cosine similarities (between centroids and query tokens) for each token.
scores.topk(4, dim=0, sorted=False).valuestensor([[0.5786, 0.9521, 0.7397, 0.7510, 0.9395, 0.5850, 0.5859, 0.9131, 0.6782,
0.5186, 0.6353, 0.7104, 0.9209, 0.9014, 0.9443, 0.9473, 0.9434, 0.9497,
0.9468, 0.9331, 0.9355, 0.9233, 0.9370, 0.9336, 0.7026, 0.9468, 0.9131,
0.7529, 0.9517, 0.9482, 0.9448, 0.9429],
[0.5361, 0.8901, 0.6255, 0.6245, 0.9097, 0.5220, 0.7354, 0.8682, 0.6260,
0.4663, 0.5654, 0.6030, 0.8486, 0.8306, 0.9429, 0.8979, 0.8950, 0.8960,
0.8965, 0.8799, 0.8892, 0.8770, 0.8794, 0.8774, 0.5869, 0.8921, 0.8418,
0.6328, 0.8931, 0.9009, 0.8970, 0.8994],
[0.7129, 0.9458, 0.4612, 0.4766, 0.9658, 0.4229, 0.5332, 0.9219, 0.7002,
0.4092, 0.4729, 0.5034, 0.9111, 0.8955, 0.8872, 0.9487, 0.9458, 0.9497,
0.9492, 0.9375, 0.9419, 0.9312, 0.9380, 0.9365, 0.4958, 0.9453, 0.9048,
0.4829, 0.9482, 0.9507, 0.9482, 0.9482],
[0.4753, 0.8882, 0.3442, 0.3616, 0.8799, 0.3958, 0.5195, 0.8589, 0.6108,
0.4077, 0.4324, 0.4333, 0.8438, 0.8281, 0.8872, 0.8945, 0.8901, 0.8955,
0.8926, 0.8745, 0.8813, 0.8687, 0.8774, 0.8745, 0.4360, 0.8911, 0.8394,
0.3711, 0.8911, 0.8955, 0.8911, 0.8916]], device='cuda:0',
dtype=torch.float16)The first value, 0.5786 represents the cosine similarity (dot product) between a centroid and the first query token.
cells = scores.topk(4, dim=0, sorted=False).indices.permute(1,0)
cells.shapetorch.Size([32, 4])The following line flattens out the 32 x 4 matrix into a 128-value 1D tensor.
cells = cells.flatten().contiguous() # (32 * ncells,)
cells.shapetorch.Size([128])The following gets the unique centroid IDs. In this case there are 10 unique centroids that give the top-4 cosine similarity with all 32 tokens.
cells = cells.unique(sorted=False)
cells.shapetorch.Size([10])cellstensor([ 7, 8, 14, 19, 24, 29, 31, 38, 41, 61], device='cuda:0')Confirming that we can recreate the cosine similarity (0.5768) betweeen the first centroid (with ID = 7) and the first query token:
(searcher.ranker.codec.centroids[7] * Q[0].T).sum()UserWarning: The use of `x.T` on tensors of dimension other than 2 to reverse their shape is deprecated and it will throw an error in a future release. Consider `x.mT` to transpose batches of matrices or `x.permute(*torch.arange(x.ndim - 1, -1, -1))` to reverse the dimensions of a tensor. (Triggered internally at ../aten/src/ATen/native/TensorShape.cpp:3683.)
(searcher.ranker.codec.centroids[7] * Q[0].T).sum()tensor(0.5786, device='cuda:0', dtype=torch.float16)ivf
The next line in generate_candidate_pids gets to the core of PLAID: the mapping between centroid IDs and passage IDs:
pids, cell_lengths = self.ivf.lookup(cells)searcher.ranker.ivf<colbert.search.strided_tensor.StridedTensor at 0x7d0a4f48e350>pids, cell_lengths = searcher.ranker.ivf.lookup(cells)
pids.shape, cell_lengths.shape(torch.Size([10]), torch.Size([10]))cellstensor([ 7, 8, 14, 19, 24, 29, 31, 38, 41, 61], device='cuda:0')pidstensor([0, 0, 1, 0, 1, 2, 2, 2, 0, 0], device='cuda:0', dtype=torch.int32)cell_lengthstensor([1, 1, 1, 1, 1, 1, 1, 1, 1, 1])How I interpret this: we have 10 centroid IDs (cells) and each are mapped to 1 passage ID. Now, given that we only have 3 passages to work with, there are some repeats (passage ID 0 corresponds to both centroid IDs 7 and 8).
I’ll leave my full exploration of how ivf is constructed for a future video/blog post, but as an aside, I do want to highlight some things I learned, starting with the fact that our index_path contains a lot of interesting files!
path = Path(index_path)
path.ls()(#12) [Path('.ragatouille/colbert/indexes/toy_example/0.residuals.pt'),Path('.ragatouille/colbert/indexes/toy_example/collection.json'),Path('.ragatouille/colbert/indexes/toy_example/pid_docid_map.json'),Path('.ragatouille/colbert/indexes/toy_example/metadata.json'),Path('.ragatouille/colbert/indexes/toy_example/buckets.pt'),Path('.ragatouille/colbert/indexes/toy_example/doclens.0.json'),Path('.ragatouille/colbert/indexes/toy_example/centroids.pt'),Path('.ragatouille/colbert/indexes/toy_example/0.codes.pt'),Path('.ragatouille/colbert/indexes/toy_example/avg_residual.pt'),Path('.ragatouille/colbert/indexes/toy_example/plan.json'),Path('.ragatouille/colbert/indexes/toy_example/0.metadata.json'),Path('.ragatouille/colbert/indexes/toy_example/ivf.pid.pt')]Each passage contains 13 tokens:
json.load(open(path/'doclens.0.json'))[13, 13, 13]For a total of 39 token embeddings:
metadata = json.load(open(path/'0.metadata.json'))
metadata{'passage_offset': 0,
'num_passages': 3,
'num_embeddings': 39,
'embedding_offset': 0}There are indeed 64 centroids.
centroids = torch.load(path/'centroids.pt', weights_only=True)
centroids.shapetorch.Size([64, 128])There exists a mapping between the 64 centroid IDs and the 39 passage token embeddings
codes = torch.load(path/'0.codes.pt', weights_only=True)
codes.shape, codes.min(), codes.max()(torch.Size([39]), tensor(0, dtype=torch.int32), tensor(61, dtype=torch.int32))There exists 39 residuals, one for each passage token! I’m not sure why there are only 64 dimensions.
residuals = torch.load(path/'0.residuals.pt', weights_only=True)
residuals.shapetorch.Size([39, 64])The values of the residuals are integers!
residuals[0][:5]tensor([191, 183, 50, 66, 203], dtype=torch.uint8)Okay, that’s enough of an aside. The final piece of interest in generate_candidates are the lines
pids, centroid_scores = self.generate_candidate_pids(Q, ncells)
sorter = pids.sort()
pids = sorter.values
pids, pids_counts = torch.unique_consecutive(pids, return_counts=True)pids, centroid_scores = searcher.ranker.generate_candidate_pids(Q, ncells=4)
pids.shape, centroid_scores.shape(torch.Size([10]), torch.Size([64, 32]))sorter = pids.sort()
sortertorch.return_types.sort(
values=tensor([0, 0, 0, 0, 0, 1, 1, 2, 2, 2], device='cuda:0', dtype=torch.int32),
indices=tensor([1, 0, 8, 3, 9, 4, 2, 7, 5, 6], device='cuda:0'))pids = sorter.values
pids, pids_counts = torch.unique_consecutive(pids, return_counts=True)
pids.shape, pids_counts.shape(torch.Size([3]), torch.Size([3]))pidstensor([0, 1, 2], device='cuda:0', dtype=torch.int32)pids_countstensor([5, 2, 3], device='cuda:0')Let’s recap what we’ve done:
- We picked a number of centroid IDs nearest to each query token that we’re interested in (
ncells = 4) - We calculated the cosine similarity between centroids and query tokens (
searcher.ranker.codec.centroids @ Q.T) - We picked the top-4 scores per query token (
scores.topk) and grabbed their indices along dim=0 (rows). - We then reduced those 32 x 4 = 128 centroid IDs down to the 10 unique ones.
- And looked them up in our index to get the corresponding 10 passage IDs.
- We reduced those to the 3 unique passage IDs.
These are our candidate passages at the end of Stage 1!
Stage 2: Centroid Interaction with Pruning
We now want to keep PIDs corresponding to centroids that exceed a minimum threshold cosine similarity with query tokens.
Now that we’ve gotten the initial candidate pids, the next line of interest in rank is:
scores, pids = self.score_pids(config, Q, pids, centroid_scores)searcher.ranker.score_pidscolbert.search.index_storage.IndexScorer.score_pids
def score_pids(config, Q, pids, centroid_scores)
Always supply a flat list or tensor for `pids`. Supply sizes Q = (1 | num_docs, *, dim) and D = (num_docs, *, dim). If Q.size(0) is 1, the matrix will be compared with all passages. Otherwise, each query matrix will be compared against the *aligned* passage.
score_pids will handle both Stage 2 and Stage 3.
Picking centroids with scores above threshold
The first important line in score_pids is the following:
idx = centroid_scores.max(-1).values >= config.centroid_score_thresholdI’ll refresh our pids and centroid_scores to the values they would have inside of rank:
Q = searcher.encode(q)
Q.shapetorch.Size([1, 32, 128])pids, centroid_scores = searcher.ranker.retrieve(searcher.config, Q)
pids.shape, centroid_scores.shape(torch.Size([3]), torch.Size([64, 32]))The centroid score threshold is set in the config
searcher.config.centroid_score_threshold0.5idx = centroid_scores.max(-1).values >= searcher.config.centroid_score_threshold
idx.shapetorch.Size([64])idx is a boolean tensor, True for rows where the maximum cosine similarity is at or above the threshold and False for where it’s under it.
idxtensor([False, False, False, False, False, False, False, True, True, False,
False, False, False, False, True, False, False, False, False, True,
False, False, False, False, False, False, False, False, False, True,
False, True, False, False, False, False, False, False, True, False,
False, True, False, False, False, False, False, False, False, False,
False, False, False, False, False, False, False, False, False, False,
False, True, False, False], device='cuda:0')Looking up codes (centroid IDs corresponding to passage tokens)
The next line of interest in score_pids is:
codes_packed, codes_lengths = self.embeddings_strided.lookup_codes(pids_)searcher.ranker.embeddings_strided<colbert.indexing.codecs.residual_embeddings_strided.ResidualEmbeddingsStrided at 0x7d0a4f48d180>A key point here, which aligns with what I understood from the paper: we are looking up centroid IDs corresponding to the passage tokens in our passage IDs. Note that there are 39 values in codes_packed which correspond to the 39 passage token embeddings. I’ll leave me exploration for how I got this conclusion for a future video/blog post.
codes_packed, codes_lengths = searcher.ranker.embeddings_strided.lookup_codes(pids)
codes_packed.shape, codes_lengths.shape(torch.Size([39]), torch.Size([3]))codes_packedtensor([41, 8, 61, 7, 7, 47, 60, 19, 19, 1, 42, 46, 41, 24, 58, 58, 14, 14,
2, 3, 60, 23, 12, 2, 16, 48, 29, 38, 31, 37, 9, 6, 57, 5, 17, 13,
0, 0, 29], device='cuda:0', dtype=torch.int32)Note that codes_lengths tells us how many tokens there are in each passage.
codes_lengthstensor([13, 13, 13])From the PLAID paper (emphasis mine):
The procedure works as follows. Recall that \(S_{c,q}\) from Equation 2 stores the relevance scores for each centroid with respect to the query tokens. Suppose \(I\) is the list of the centroid indices mapped to each of the tokens in the candidate set. Furthermore, let \(S_{c,q}\) denote the i-th row of \(S_{c,q}\). Then PLAID constructs the centroid-based approximate scores \(\tilde{D}\) as:
Picking scores for centroid IDs corresponding to passage tokens
The next line in score_pids does just that: pick the centroid IDs that correspond to the passage tokens of interest:
idx_ = idx[codes_packed.long()]
idx_.shapetorch.Size([39])idx_tensor([ True, True, True, True, True, False, False, True, True, False,
False, False, True, False, False, False, True, True, False, False,
False, False, False, False, False, False, True, True, True, False,
False, False, False, False, False, False, False, False, True],
device='cuda:0')We then use this to index back into codes_packed to select the centroid IDs that are at or above the threshold of 0.5. There are 14 such centroid IDs.
codes_packed_ = codes_packed[idx_]
codes_packed_, codes_packed_.shape(tensor([41, 8, 61, 7, 7, 19, 19, 41, 14, 14, 29, 38, 31, 29],
device='cuda:0', dtype=torch.int32),
torch.Size([14]))Finally, we can index into our scores and pick out the scores that correspond to these centroid IDs:
approx_scores_ = centroid_scores[codes_packed_.long()]
approx_scores_.shapetorch.Size([14, 32])We now have the scores between 14 centroids that are mapped to our candidate passage ID’s tokens and all 32 query tokens.
Max-reducing scores to get 1 score per passage ID
The last step of Stage 2 is to max-reduce the scores down to 1 per passage. The following lines are of interest:
pruned_codes_strided = StridedTensor(idx_, codes_lengths, use_gpu=self.use_gpu)
pruned_codes_padded, pruned_codes_mask = pruned_codes_strided.as_padded_tensor()
pruned_codes_lengths = (pruned_codes_padded * pruned_codes_mask).sum(dim=1)
...
approx_scores_strided = StridedTensor(approx_scores_, pruned_codes_lengths, use_gpu=self.use_gpu)
approx_scores_padded, approx_scores_mask = approx_scores_strided.as_padded_tensor()
approx_scores_ = colbert_score_reduce(approx_scores_padded, approx_scores_mask, config)from colbert.search.strided_tensor import StridedTensor, StridedTensorCoreidx_.shapetorch.Size([39])pruned_codes_strided = StridedTensor(idx_, codes_lengths)
pruned_codes_strided<colbert.search.strided_tensor.StridedTensor at 0x7d0a4f688e20>pruned_codes_padded, pruned_codes_mask = pruned_codes_strided.as_padded_tensor()
pruned_codes_padded.shape, pruned_codes_mask.shape(torch.Size([3, 13]), torch.Size([3, 13]))pruned_codes_paddedtensor([[ True, True, True, True, True, False, False, True, True, False,
False, False, True],
[False, False, False, True, True, False, False, False, False, False,
False, False, False],
[ True, True, True, False, False, False, False, False, False, False,
False, False, True]], device='cuda:0')My understanding of StridedTensor is still spotty, but from what I can see it allows the reshaping of values from a 1-D 39 to 3 x 13. In this way, we are organizing centroid IDs by both passage ID and by passage token.
pruned_codes_lengths = (pruned_codes_padded * pruned_codes_mask).sum(dim=1)
pruned_codes_lengthstensor([8, 2, 4], device='cuda:0')There are 8 centroids corresponding to tokens in the first passage that cross the score threshold, 2 for the second passage and 4 for the third.
Note that pruned_codes_mask is True everywhere so multiplying pruned_codes_padded by it keeps all of its values intact:
pruned_codes_masktensor([[True, True, True, True, True, True, True, True, True, True, True, True,
True],
[True, True, True, True, True, True, True, True, True, True, True, True,
True],
[True, True, True, True, True, True, True, True, True, True, True, True,
True]], device='cuda:0')The next lines reshapes our approx_scores_ similarly.
approx_scores_.shapetorch.Size([14, 32])approx_scores_strided = StridedTensor(approx_scores_, pruned_codes_lengths)
approx_scores_padded, approx_scores_mask = approx_scores_strided.as_padded_tensor()
approx_scores_padded.shape, approx_scores_mask.shape(torch.Size([3, 8, 32]), torch.Size([3, 8, 1]))What’s interesting to note here is approx_scores_mask. We know from pruned_codes_lengths that there are 8 centroid IDs for the first passage, 2 for the second, and 4 for the third. approx_scores_mask flags True for valid values and False for padding values.
approx_scores_masktensor([[[ True],
[ True],
[ True],
[ True],
[ True],
[ True],
[ True],
[ True]],
[[ True],
[ True],
[False],
[False],
[False],
[False],
[False],
[False]],
[[ True],
[ True],
[ True],
[ True],
[False],
[False],
[False],
[False]]], device='cuda:0')We then pass these padded scores to colbert_reduce which performs the famous MaxSim operation:
from colbert.modeling.colbert import colbert_score, colbert_score_packed, colbert_score_reduceapprox_scores_ = colbert_score_reduce(approx_scores_padded, approx_scores_mask, searcher.config)
approx_scores_tensor([27.2812, 12.9844, 22.1719], device='cuda:0', dtype=torch.float16)Note that these are not the same values as our RAGatouille results. Instead, these are intermediate scores.
Taking a look at colbert_score_reduce there are four main lines of interest in my opinion:
D_padding = ~D_mask.view(scores_padded.size(0), scores_padded.size(1)).bool()
scores_padded[D_padding] = -9999
scores = scores_padded.max(1).values
scores.sum(-1)D_padding = ~approx_scores_mask.view(approx_scores_padded.size(0), approx_scores_padded.size(1)).bool()
approx_scores_padded[D_padding] = -9999
approx_scores_padded.shapetorch.Size([3, 8, 32])We take the max along dim=1, which is the dimension with centroid IDs corresponding to passage tokens. So, in other words, we are finding the maximum score between centroid and query token for each query token per passage.
scores = approx_scores_padded.max(1).values
scores.shapetorch.Size([3, 32])Finally, we sum across query tokens per passage ID.
scores.sum(-1)tensor([27.2812, 12.9844, 22.1719], device='cuda:0', dtype=torch.float16)Picking the top-ndocs passages
The last step is to pick the top-ndocs passage IDs.
searcher.config.ndocs256ndocs is 256, much larger than the number of passages we have, so I’ll rank with k=3:
if searcher.config.ndocs // 4 < len(approx_scores_):
pids = pids[torch.topk(approx_scores_, k=(searcher.config.ndocs // 4)).indices]pids = pids[torch.topk(approx_scores_, k=3).indices]
pidstensor([0, 2, 1], device='cuda:0', dtype=torch.int32)To recap Stage 2:
- We select centroid IDs that were both at/above our threshold of 0.5 AND corresponded to passage tokens for the passage IDs in our initial candidate pool from Stage 1.
- We then do some reshaping so we can calculate the MaxSim score for each passage ID.
- We pick the top-
ndocspassages.
Stage 3: Centroid Interaction w/o Pruning
We now have our candidate set from Stage 2. We lookup the centroid IDs for the passage tokens in these passage IDs:
codes_packed, codes_lengths = searcher.ranker.embeddings_strided.lookup_codes(pids)
codes_packed.shape, codes_lengths.shape(torch.Size([39]), torch.Size([3]))We don’t use the threshold for this step—all centroids, even those who have a maximum cosine similarity with query tokens being less than our threshold:
approx_scores = centroid_scores[codes_packed.long()]
approx_scores.shapetorch.Size([39, 32])Note how we are now dealing with 39 centroids, not 14 like we did in Stage 2.
We do the same reshaping/padding as we did in Stage 2, and use colbert_score_reduce again:
approx_scores_strided = StridedTensor(approx_scores, codes_lengths)
approx_scores_padded, approx_scores_mask = approx_scores_strided.as_padded_tensor()
approx_scores = colbert_score_reduce(approx_scores_padded, approx_scores_mask, searcher.config)
approx_scorestensor([27.2812, 22.1875, 13.7266], device='cuda:0', dtype=torch.float16)We then pick the top-ndocs//4 passage IDs, in this case all 3 of our passage IDs.
if searcher.config.ndocs // 4 < len(approx_scores):
pids = pids[torch.topk(approx_scores, k=(searcher.config.ndocs // 4)).indices]pids = pids[torch.topk(approx_scores, k=3).indices]
pidstensor([0, 2, 1], device='cuda:0', dtype=torch.int32)This is the candidate set at the end of Stage 3. Note that the scores are still not quite the same as RAGatouille, as these are intermediate scores.
Stage 4: Final ranking with decompression
We’re now in the final Stage of the PLAID scoring pipeline. We now get the full 128-dimension vectors for all of our passage ID’s tokens:
D_packed, D_mask = searcher.ranker.lookup_pids(pids)
D_packed.shape, D_mask.shape(torch.Size([39, 128]), torch.Size([3]))D_packed[0][0]tensor(-0.0102, device='cuda:0', dtype=torch.float16)Since we only have one query:
Q.size(0)1We use the following lines of code:
colbert_score_packed(Q, D_packed, D_mask, searcher.config)tensor([27.6875, 22.2812, 13.9531], device='cuda:0', dtype=torch.float16)Looking into colbert_score_packed, here are the lines of interest:
Q = Q.squeeze(0)
Q.shapetorch.Size([32, 128])We calculate the cosine similarity between each passage token and each query token:
scores = D_packed @ Q.to(dtype=D_packed.dtype).T
scores.shapetorch.Size([39, 32])Reshape them so we can max-reduce them by passage ID:
scores_padded, scores_mask = StridedTensor(scores, D_mask).as_padded_tensor()
scores_padded.shape, scores_mask.shape(torch.Size([3, 13, 32]), torch.Size([3, 13, 1]))And max-reduce with colbert_score_reduce:
colbert_score_reduce(scores_padded, scores_mask, searcher.config)tensor([27.6875, 22.2812, 13.9531], device='cuda:0', dtype=torch.float16)This matches exactly the scores we got using RAGatouille!
results[{'content': 'Python is a programming language. It is easy to learn',
'score': 27.6875,
'rank': 1,
'document_id': '8aa5aade-10d5-4144-b634-c7866578b43c',
'passage_id': 0},
{'content': 'Python was created by Guido van Rossum in 1991',
'score': 22.28125,
'rank': 2,
'document_id': '12352328-9bb1-4a51-896e-a002d3548adc',
'passage_id': 2},
{'content': 'Java is a popular coding language used in many applications',
'score': 13.953125,
'rank': 3,
'document_id': '1fe9788e-ccec-4b9e-a004-14acc657915e',
'passage_id': 1}]To recap Stage 4:
- We lookup the full vectors corresponding to all passage tokens in our passage IDs.
- We reshape them to allow for max-reduction by passage ID.
- We calculate the MaxSim score for each passage.
In this way, we were able to recreate the entire 4-stage PLAID pipeline to match RAGatouille results!